11) Линейное однородное дифференциальное уравнение n-го порядка.

Опр:Линейным дифференциальным уравнением n-го порядка называется уравнение, линейное относительно неизвестной функции и ее произ­водных и, следовательно, имеющее вид(1)

где а0(х),а1(х)_,…аn(х)-коэф.уравнения

Опр:Если правая часть f(х)≡0, то уравнение(1) называется линейным однородным, так как оно однородно относительно неизвестной функции у и ее производных.

Если, то разделив обе части (1)на эту функцию:

Опр:Ур.(3) наз линейным n-порядка в нормальной форме(коэф. при старшей произв.=0)

Если все коэф.(3) фун.(i=0…n) и f(x) непрерывны на ,то ур (3) в любой окрестности начальных значений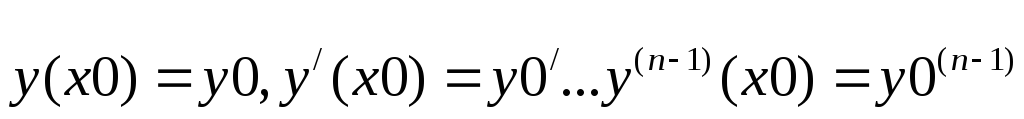гдеудовлетворяет условия м теоремы существования единственности решений.

Условия выполнения:

1) явл .непр. относительно всех аргументов т.к.она линейная комбинация непрерывных функций.

2)Т.К. коэф.pi непрерывны на, то по теореме Вейерштрасса, они на этом же отрезке ограничены.

Основные св-ва частных решений лин. однор.ур.

Речь пойдет об ур (2).

1)Если фун. у(х) явл. решением лин. однор. ур(2), то новая функция Су(х) явл. решением этого же уравнения.

Док-во.

Подставим Су(х) в левую часть (2).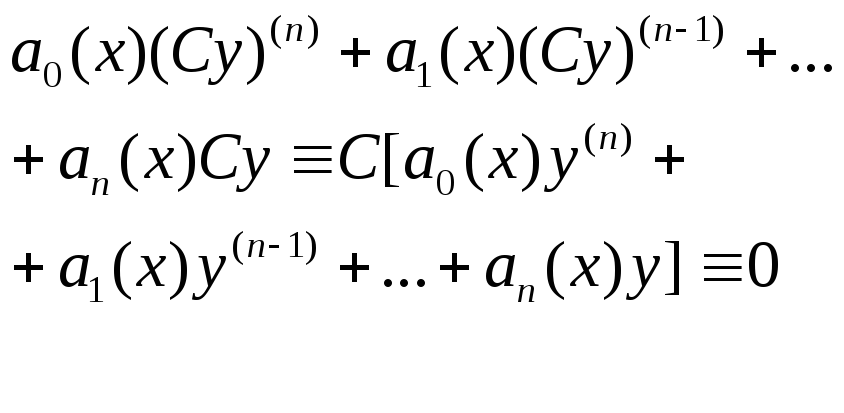2)Если у1(х),у2(х) явл. решением одного и того же лин. однор. ур(2), то их сумма у1(х)+у2(х), то же решение его же.

Док-в0.

Подставим новую фун. в левую часть ур(2).

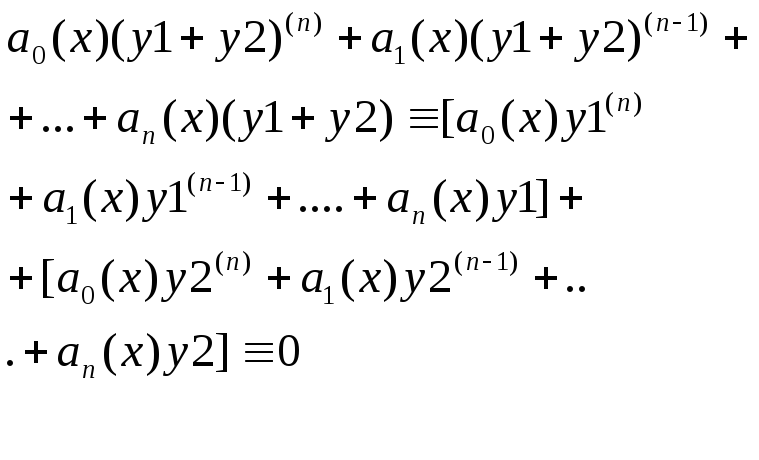3)Если фун. m: у1(х),у2(х)…yn(x) явл. решением одного и того же лин. однор. ур. (2), то их линейная комбинация также явл. решением (2)

Док-во.

Очевидно.

4)Если (2)с действ. коэффициентами ai(i=0…n)имеет комплексно значное решение y(x)=u(x)+iv(x), то u(x),v(x) –вещ-ые по отдельности явл. решениями того же ур-я.

Док-во.

Подставим у в Ур-е. 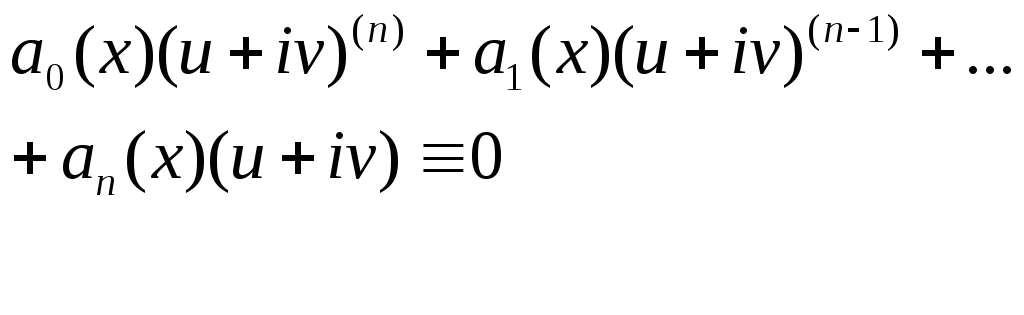Воспользуемся свойством линейности производной любого порядка.

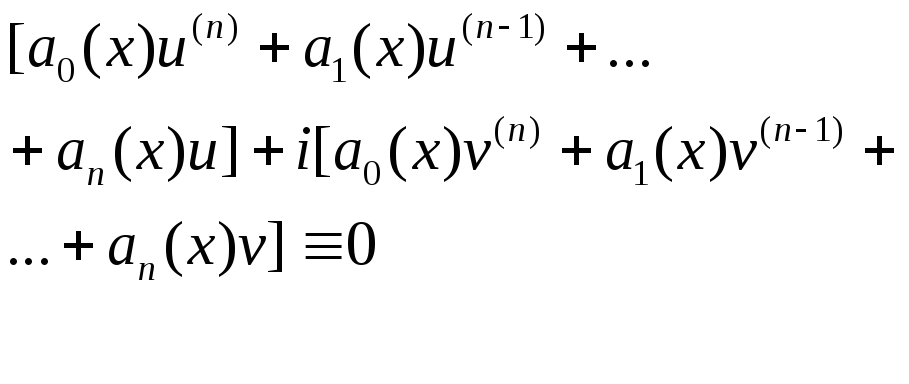[]-вещ.функция.

Основное св-во комплексно значных функции.

Комплексно значные фун.Тогда, когдаее вещественная и мнимая часть.

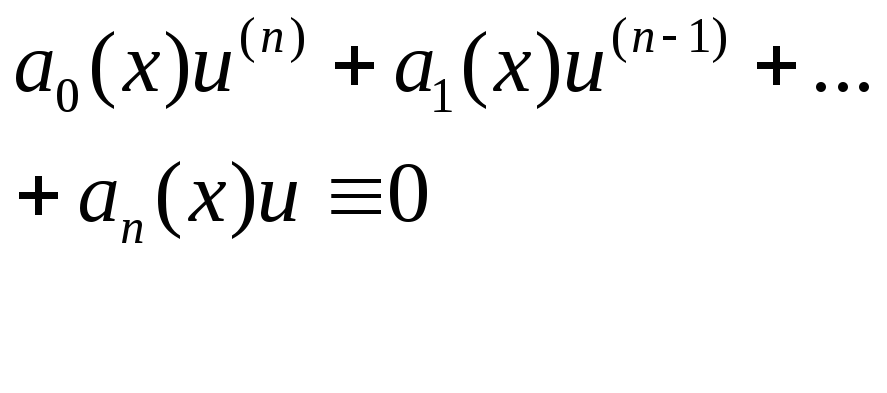
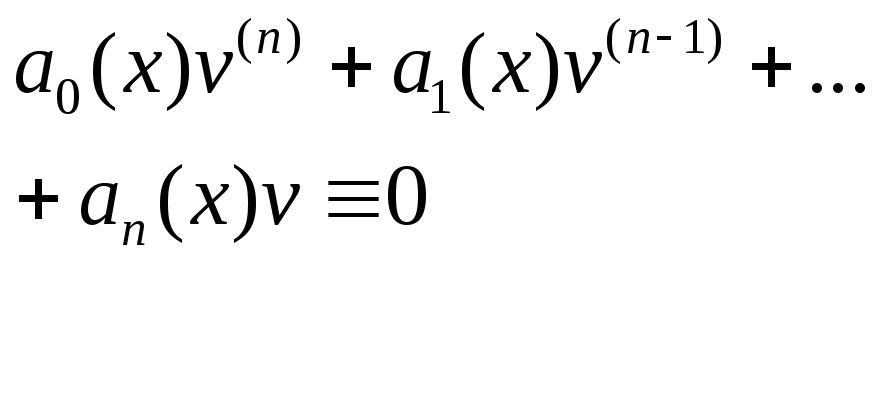
u,v-решения (2).у1(х)…уn(х)наз лин. зав. на , если

справедливо а1у1(х)+…+аnyn(х)(5)

Опр (лин. нез.): у1(х)…уn(х) наз. лин. незав. на, для них (5) выполнено когда а1=…=аn=0.

Пр: рассм .Докажем, что явл. лин.нез.на любом отрезке.

Док-во

Пусть.Фун лин.зав., то по опр

Т.к среди коэф. есть один,то левая часть есть многочлен не вышеn, то из алгебры известна т-ма:Мн-ны степени n имеют не более n различных корней, то мн-н может быть=0 не более чем в n различных точек, то тождество невозможно, то противоречие.

Опр(лин.зав.):

.

12) Определитель Вронского линейного однородного дифференциального уравнения n-го порядка и его основные свойства свойства.

Определение. Если заданы диф. функцией y₁(x),y₂(x),…,y_n(x), то функциональный определитель: 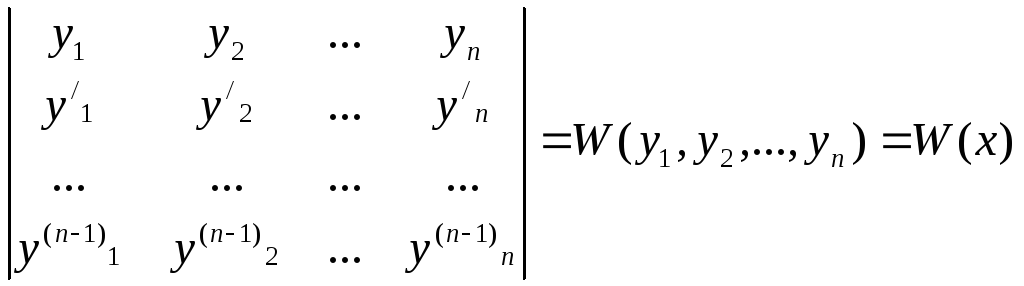называется определителем Вронского нашихn-функций.

Основные свойства определителя Вронского.

Свойства: 1. Если y₁(x),y₂(x),…,y_n(x), являются линейно зависимыми на [a,b], то .

Док-во.

Опр лин.зав. :

(6)

…………………………………………………

Система (6) явл. линейной,однор, алгебраической.Определитель каждой совпадает с определителем Вронского.

В курсе алгнбры доказана след. теорема: лин,однор,алгебр. сис-ма имеет не тривиальное решение. То (6) имеет нетрив. решение.Т.к. среди ai есть хотя бы одна=0.То по теореме опедел. Вронского

2. Если y₁(x),y₂(x),…,y_n(x), являются линейно независими на [a,b] частными решениями линейной однородного Ур-я:

док-во.

Пусть в некоторой точке нашего отрезка

(8)

…………………………………………….

То по алгебр.теореме (8) имеет нетривиальное решение.

Возьмем какое-нибудь из них а1,а2,…an,ai=0

то по 3 св-ву частных решений лин. однор. Ур. у(х) является решением(7).

Это решение удовлетворяет:

Очевидно (7) имеет решение

удовлетворяет условиям (9).При сформулир. условиях (7) удовлетворяет условию теор. существ. и единств. рения.

То существует одно решение ур. (7) которое удовлетворяет условиям (9).

.А это невозможно т.к. функция у1,у2….на лин.нез..То противоречие.

Дополнительное требование:yi явл. решениями одного и того же ур. с непр. коэф. и отказаться от условия нельзя.

Покажем, что w на [0,2]

Наши фукции лин.нез. на [0,2]т.к.

а1=0

а2=0,то выполняется тождество,то обе константы=0.