1.3. Свойства линейных операций над векторами

1. +=+– коммутативное (переместительное) свойство сложения.

2. (+)+=+(+) – ассоциативное (сочетательное) свойство сложения.

3.  =() – ассоциативное относительно числового множителя свойство.

4.  (+) =+– дистрибутивное (распределительное) относительно суммы векторов свойство.

5.(+)=+– распределительное свойство относительно суммы чисел.

Докажем свойство 3: Если хотя бы одно из чисел   или вектор равны нулю, то обе части этого равенства обращаются в нуль. Если, ,то векторы  и коллинеарны, одинаково направлены (их направления либо совпадают с направлением вектора,если и имеют одинаковый знак, либо противоположны направлению вектора, еслии  разных знаков) и имеют одинаковые длины  и

,следовательно, они равны. 

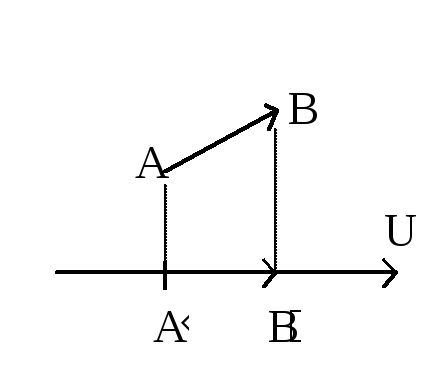
1.4. Проекция вектора на ось

Пусть в пространстве заданы ось (прямая с выбранным на ней направлением ) и некоторый вектор . Проведем через точки А и В плоскости, перпендикулярные осиU. Обозначим через А^/ и В^/ точки пересечения этих плоскостей с осью

Определение:Проекцией (геометрической ) вектора на осьU называется вектор А^/В^/, начало которого А^/ – есть проекция начала А на ось U ,а конец В^/ - проекция конца В на ту же ось. Обозначается проекция так: Пр _u или, короче,Пр_.

Определение: Проекцией (алгебраической) векторана осьU называется длина вектора А^/В^/, взятая со знаком «+», если его направление совпадает с направлением оси u и со знаком «–», если их направления противоположны.

Обозначение: ПРuилиПР

Замечание 1: Геометрическая проекция (или компонента) вектора есть вектор, а алгебраическая проекция вектора есть число.

Замечание 2: В задачах, требующих найти проекцию вектора, обычно, имеют в виду алгебраическую проекцию.

Имеет место следующая теорема.

Теорема 1: Проекция вектора на осьu равна длине вектора , умноженной на косинус угла между вектороми осьюu,т. е. ПР_u=cos  (1) , где  – угол между вектором и осьюu

Доказательство: Если     (на рисунке под а)), то в силу определения проекции имеем

ПР_ОХ=А^/ В ^/ = cos  .

Если же    , (см. рис. в)), то в силу вновь определения

проекции имеем ПР_ОХ= –А^/ В ^/ = –cos= =cos . Таким образом, для любого угла  справедливо данное равенство. 

Следствие 1: Проекция вектора на ось положительна (отрицательна), если вектор образует с осью острый (тупой) угол, и равна нулю, если этот угол прямой.

Следствие 2: Пусть =и задана осьl . Тогда справедливо равенство ПР_u= ПР_u, т.е. равные векторы имеют равные проекции на одну и ту же ось.

1.5. Проекции вектора на оси координат

Пусть в пространстве задана прямоугольная система координат Охуz и произвольный вектор . Пусть, далее, Х=ПР_х, У=ПР_у,Z=ПР_z (2). Проекции Х, У,Z вектора на оси координат называют его координатами. При этом принята запись=.

Теорема 2: Каковы бы ни были две точки А (х_1у_1z₁) и В (х_2у_2z₂), координаты вектора определяются следующими формулами: Х=х₂- х_{1 ,} У = у₂ – у₁, Z = z₂ – z_1. Другими словами, чтобы найти координаты вектора, если известны координаты начала вектора и его конца, надо из координат конца вектора вычесть соответствующие координаты начала вектора.

Доказательство: Поведем через точки А и В плоскости, перпендикулярные оси Ох, и обозначим точки пересечения с осью Ох соответственно через А^/ и В^/. Точки А^/ и В^/ на оси Ох имеют координаты х₁ и х₂

z

А В

х

у

По определению, Х = ПР_х = А^/В^/. Но А^/В^/ =х₂ – х_1. Поэтому Х=х ₂– х_. Аналогично устанавливаются и остальные формулы. 

Замечание: Если вектор выходит из начала координат, т. е. х₁=у₁=z₁=0, и х₂=х, у₂=у, z₂=z, то координаты Х, У,Z вектораравны координатам его конца: Х = х, У = у,Z =z.