
Физпрактикум.Оптика
.pdf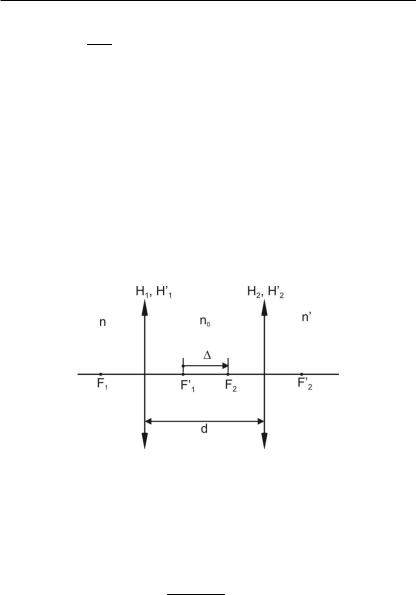
1.5. Центрированные оптические системы |
21 |
Из последнего соотношения следует, что
(# ( % ( '#'# & (1.29)
,
Из (1.28) и (1.29) получим:
*) |
% '# |
'" , ( '# |
& |
(1.30) |
|
, |
|||||
|
|
|
|
Аналогично можно найти расстояние ХН:
* ) |
% '" |
'" , ( '# |
& |
(1.31) |
|
, |
|||||
|
|
|
|
Обратите внимание, что f1 + c Ð f2 = H1 H2.
H1 H2 Ð расстояние от второй главной плоскости первой системы до первой главной плоскости второй системы.
Частные случаи оптических систем
I. Система из двух тонких линз (рис. 1.15).
!"#. #.#+. D"#%).' "6 4/15 %-*7"5 ,"*6
На рис. 15 n, n0, n Ð показатели преломления соответствующих сред. Согласно рис. 1.15
c = d Ð f1 + f2, (1.32)
где f1 Ð второе фокусное расстояние первой линзы; f2 Ð первое фокусное расстояние второй линзы.
Подставив (1.32) в (1.26), найдем:
' % '"'# + откуда
, ( '" '#

22 |
|
|
|
|
|
|
|
|
|
Тема 1. Геометрическая оптика |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
- |
|
|
- |
|
|
- ' |
# |
|
,- |
|
|
|
|||
|
|
% |
|
|
( |
|
|
( |
|
|
& |
(1.33) |
|||
' |
|
' |
|
|
|
|
|
|
|
||||||
|
|
# |
|
'"' |
# |
|
'"' |
# |
|
|
|||||
Учтем, что
а) n /f = Ф Ð оптическая сила системы 2 тонких линз; б) n /f 2 = Ф2 Ð оптическая сила второй линзы;
|
|
|
% |
"$! |
|
% |
"! |
|
$! |
|
$! |
|
|
|
$! |
|
|
|
|
|
||||||||
|
|
|
|
|
$! |
|
|
|
|
|
|
|
|
|
||||||||||||||
в) |
" |
|
|
# |
|
|
|
|
|
|
|
|
|
# |
|
|
|
|
|
# !# " оптическая сила первой линзы; |
||||||||
|
! ! |
|
|
|
|
! ! |
|
|
|
! |
|
|
||||||||||||||||
|
|
|
%#% |
" |
|
|
|
|
|
%#% |
" |
|
|
|
|
|
%# |
|
|
|
|
|
||||||
г) |
%$! |
" |
% |
|
# |
$ |
! |
# |
$! |
|
" |
|
% |
!"!# |
& ! |
|||||||||||||
|
|
! ! |
$! |
|
|
|
! |
' |
! |
|
|
|
|
! |
||||||||||||||
|
'"'# |
|
|
|
|
|
'" |
|
|
# |
|
$ |
|
|
||||||||||||||
Из (1.33) получим формулу для оптической силы системы двух тонких линз:
! ! !! " !" # |
$ |
!!!" % ! |
(1.34) |
|
&# |
||||
|
|
|
Из формулы (1.34) следует, что в некоторых случаях оптическая сила системы может стать равной нулю (Ф = 0). Такая система называется телескопической. Параллельный пучок света после прохождения такой системы сохраняет параллельность.
Из (1.30) и (1.31) с учетом формул (а, б, в, г) получим следующие соотношения:
#!! |
" # |
"! |
$ |
$ |
% #! |
" |
"" |
$ |
$ |
|
&! |
(1.35) |
|
" |
'# '! |
" |
'# |
' |
|||||||||
|
|
|
|
|
|
|
|
Эти формулы позволяют рассчитать расположение главных плоскостей системы двух тонких линз. Если система находится в воздухе, то n = n0 = n = 1 и оптическая сила системы будет равна:
Ф = Ф1 |
+ Ф2 |
Ð dФ1Ф2. |
(1.36) |
|||||||||
Из (1.36) следует, что в этом случае |
|
|||||||||||
" |
|
" |
" |
, |
|
& |
(1.37) |
|||||
|
|
|
% |
|
|
|
|
( |
|
|
||
' |
|
|
|
|
|
|
||||||
|
|
'" |
' |
# |
'"' |
# |
|
|
||||

1.5. Центрированные оптические системы |
23 |
II. Толстая линза (рис. 1.16).
!"#. #.#,. M-,#%'G ,"*6'
В соответствии с выводами, проведенными в п. 1, оптическая сила толстой линзы может быть вычислена по формуле (1.34), где Ф1, Ф2 Ð оптические силы первой и второй преломляющих поверхностей, d Ð толщина линзы, n0 Ð показатель преломления вещества линзы. Для толстой линзы справедливы также формулы (1.35).
III. Тонкая линза.
Линза называется тонкой, если обе ее вершины (О1 и О2) можно считать совпадающими (рис. 1.17), т. е. если ее толщина d мала по сравнению с радиусами кривизны ограничивающих поверхностей r1 и r2.
Точка О носит название оптического центра линзы.
Так как d ; 0 (cм. (1.34)), то оптическая сила тонкой линзы Ф равна сумме оптических сил Ф1, и Ф2, ограничивающих ее сферических поверхностей:
Ф = Ф1 + Ф2. (1.38)
Материалом для линз, употребляемых в видимой области света, служит стекло, в ультрафиолетовой Ð главным образом кварц, в инфракрасной Ð кварц, каменная соль, KCl и др.
!"#. #.#-. M-*7'G ,"*6' " 5-4 ,12)< / *)<

24 Тема 1. Геометрическая оптика
Пусть А1 Ð точечный объект, расположенный на главной оси системы. Если бы имелась лишь эта одна поверхность, то изображение получилось бы в точке А1 . Это изображение надо рассматривать как объект для второй преломляющей поверхности. Его изображение получится в некоторой точке А2 . Вместе с тем А2 будет изображением объекта А1, даваемым совокупностью обеих преломляющих поверхностей.
Для данной линзы заданы радиусы кривизны ее поверхностей r1 |
|||||||||||||||
и r2 и коэффициент преломления n вещества, из которого она сделана. |
|||||||||||||||
Находя по формуле (1.10) Ф1, и Ф2, получим оптическую силу тонкой |
|||||||||||||||
линзы: |
|
|
# |
1 |
1 |
$ |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||||||
! % !# & |
1"' |
|
|
& |
|
(. |
|
|
|
|
(1.39) |
||||
$ |
$ |
|
|
|
|
||||||||||
|
|
|
) |
1 |
2 |
* |
|
|
|
|
|
||||
Повторяя рассуждения, приведенные выше для одной преломляю- |
|||||||||||||||
щей поверхности, найдем фокусные расстояния тонкой линзы: |
|||||||||||||||
|
# |
|
|
! |
|
|
|
|
|
! |
|
|
|
|
|
# |
$ %# $ ! |
|
$ |
|
|
& |
! |
|
! |
' |
$ ! |
||||
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
!n %!"( |
|
% |
|
) |
(1.40) |
||
|
|
|
|
|
|
|
|
&! |
|
||||||
|
|
|
|
|
|
|
|
|
|
* |
|
&" + |
|
||
Если линза находится в среде с показателем преломления n , отличным от 1, то формула (1.40) будет иметь вид:
f ! " |
1 |
" |
|
|
1 |
|
|
|
|
. ! |
|
! |
# % |
$ |
# |
1 |
|
1 |
$ |
||||
|
|
& |
|
%1' |
& |
|
% |
|
' |
(1.40а) |
|
|
|
( %! |
) |
( |
& |
|
& |
) |
|
||
|
|
|
|
|
|
1 |
|
2 |
|
||
Если Ф > 0, то мы имеем дело с собирательной (положительной) линзой: параллельный пучок света после преломления в линзе собирается в ее первом фокусе. Если Ф < 0, то мы имеем дело с рассеивающей (отрицательной) линзой: параллельный пучок света после преломления в линзе образует расходящийся пучок лучей, продолжения которых пересекаются в первом главном фокусе.
Построение изображения в тонкой линзе. Увеличение
Будем считать линзу идеальной оптической системой.
Для определения положения точки изображения необходимо из сопряженной точки предмета в оптическую систему направить два луча. В месте их пересечения по выходу из системы и будет располагаться точка изображения. Оптическую систему располагаем в однородной среде.
1.5. Центрированные оптические системы |
25 |
|
|
!"#. #.#/. ;-#%&-)*") "6-:&'()*"G / %-*7-< ,"*6). ;&"). +)&/=<
!"#. #.#1. ;-#%&-)*") "6-:&'()*"G / %-*7-< ,"*6). ;&"). /%-&-<
Для нахождения положения изображения применяют несколько приемов.
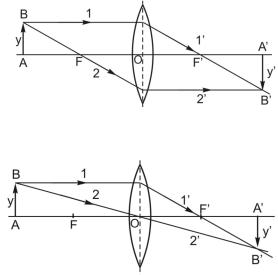
Прием первый (рис. 1.18): из точки В предмета АВ, находящейся вне оптической оси, в оптическую систему направляют два луча.
Луч 1 направляется параллельно оптической оси. Выйдя из линзы, преломленный луч 1 должен пройти через точку заднего фокуса F . Луч 2 направляется через точку переднего фокуса. Выйдя из линзы, преломленный луч 2 пойдет параллельно оптической оси. Точка В является изображением точки В. Опустив из точки В на ось перпендикуляр, мы получим изображение y предмета y.
Прием второй (рис. 1.19): из точки В предмета АВ, находящейся вне оптической оси, в систему направляются также два луча, луч 1 идет параллельно оптической оси, луч 2 Ð через оптический центр линзы О.
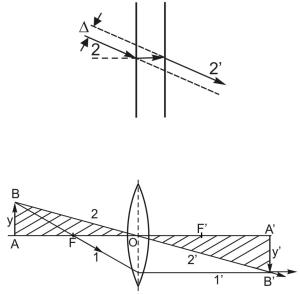
Так как линза тонкая, то для луча 2 участки обеих поверхностей можно считать параллельными, поэтому луч, проходя через них, не меняет направления, но лишь смещается параллельно самому себе (рис. 1.20). Так как толщиной линзы мы пренебрегаем, то это смеще-
26 |
Тема 1. Геометрическая оптика |
|
|
!"#. #.$2. N',-) #.)H)*") ,12'3 +&-5-4GH)0- 2)&)6 -+%"2)#7"< 3)*%& %-*7-< ,"*6=
!"#. #.$#. ;-#%&-)*") "6-:&'()*"G / %-*7-< ,"*6). ;&"). %&)%"<
ние , ничтожно мало, и луч 2 проходит практически без преломления, переходя в луч 2 . Точка пересечения лучей 1 , 2 даст изображение точки В.
Прием третий (см. рис. 1.21). Третий прием нахождения изображения ясен из анализа двух предыдущих. Из подобия заштрихованных треугольников и (1.23) следует, что линейное увеличение
) = S /S. |
(1.41) |
1.6. Аберрации линз
Для получения идеального изображения необходимо выполнение следующих условий:
1)параксиальность пучков света (их близость к оптической оси линзы и малость углов, составляемых лучами с оптической осью;
2)монохроматичность света.
Невыполнение этих условий приводит к появлению погрешностей изображения (аберраций), которые значительно снижают его качест-
1.6. Аберрации линз |
27 |
во. В современных оптических приборах путем подбора соответствующих комбинаций линз или изменения формы их поверхностей удается устранить большинство из наиболее важных в данных условиях аберраций.
Рассмотрим некоторые наиболее важные и часто встречающиеся аберрации линз.
Астигматизм косых пучков
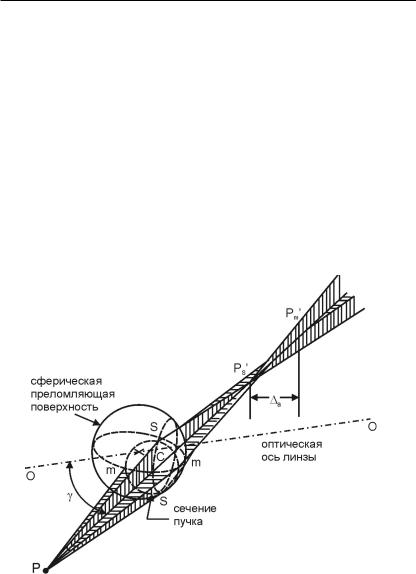
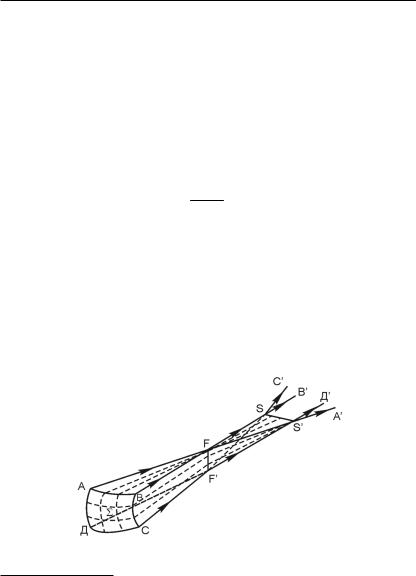
Астигматизмом называется аберрация, выражающаяся в том, что лучи одного и того же гомоцентричного (имеющего одну точку схождения) пучка после преломления в линзе собираются не в одну точку, а образуют две ортогональные прямые. Это наблюдается в том случае, когда пучок лучей, падающий на линзу, составляет значительный угол с ее оптической осью. Для того чтобы понять происхождение этой аберрации, рассмотрим преломление на сферической поверхности линзы узкого пучка лучей, исходящих из некоторой точки Р (рис. 1.22).
!"#. #.$$. @#%"0.'%"6. 7-#=5 +127-/
28 |
Тема 1. Геометрическая оптика |
Средний луч РС пучка падает в точку С сферической поверхности под углом α к оптической оси. Плоскость, проходящая через оптическую ось линзы и средний луч пучка, называется меридиональной плоскостью. Лучи, лежащие в этой плоскости, называются соответственно меридиональными. Они пересекают поверхность по меридиану ÒmmÓ. Плоскость PSS, проходящая через средний луч пучка перпендикулярно меридиональной плоскости, и лучи, лежащие на ней, называются сагиттальными. Они пересекают преломляющую сферу по ÒпараллелиÓ SS (рис. 1.22). Радиусы кривизны параллели rS и меридиана rm различны. Как известно, оптическая сила Ф сферической поверхности определяется формулой
! # !! " ! " !
#
где r Ð радиус кривизны поверхности; n и n Ð показатели преломления разделяемых ею сред.
Так как rm > rS, то Фm < ФS, следовательно, меридиональные лучи пересекутся дальше от поверхности, чем сагиттальные. Это значит, что преломление косого (α ≠ 0) пучка лучей на сферической поверхности сопровождается нарушением его гомоцентричности.
Волновая поверхность негомоцентрического пучка не является сферической. На рис. 1.23 изображен элемент Σ несферической волновой поверхности преломленного пучка, ограниченной линиями кривизны− АВ, ВС, СД, АД.
!"#. #.$(. O,).)*% *)#?)&"2)#7-< /-,*-/-< +-/)&5*-#%" +&),-.,)**-0- +127'
* Линии, нормальные сечения вдоль которых имеют наибольшую или наименьшую для данной точки поверхности кривизну, называются линиями кривизны.

1.6. Аберрации линз |
29 |
Радиусы кривизны этих линий различны, поэтому лучи, являющиеся нормалями к ним, сходятся в разных точках. Лучи, ортогональные к линиям АВ, É, ДС, сходятся в соответственных точках отрезка FF , а лучи, ортогональные к линиям ВС, É, АД, Ð в соответственных точках отрезка SS . Отрезки FF и SS перпендикулярны к плоскостям, в которых лежат образующие их лучи. Отсюда следует, что меридиональные и сагиттальные лучи после преломления дают изображение светящейся точки в виде двух линий, перпендикулярных к этим плоскостям.
Расстояние cа между точками схода меридиональных и сагиттальных лучей называется астигматической разностью (рис. 1.22). Она и является мерой астигматизма.
Так как линза представляет собой совокупность двух сферических поверхностей, то все рассуждения, проведенные выше для одной сферической поверхности, справедливы и для линзы.
Для пучка лучей, идущего вдоль оптической оси линзы астигматизм отсутствует, так как кривизна всех нормальных сечений сферической поверхности одинакова.
Сферическая аберрация
Сферическая аберрация заключается в том, что точка, лежащая на оптической оси, изображается не точкой, а отрезком, вытянутым вдоль оптической оси. Сферическая аберрация также связана с нарушением гомоцентричности светового пучка при преломлении и возникает в том случае, когда изображение светящейся точки формируется широким пучком лучей.
На рис. 1.24 показан ход лучей, падающих на плоско-выпуклую линзу параллельно ее главной оптической оси. Видно, что с ростом h углы падения лучей i на сферическую поверхность линзы увеличиваются, а точка схождения лучей монотонно приближается к сферической поверхности−.
Очевидно, на экране, расположенном в области локализации от-
резка / / + изображение точки получится в виде кружка с неоднород-
" .
ным распределением освещенности.
За меру сферической аберрации принимается величина отрезка !
/ / % , !между точками схода нулевых (параксиальных) и крайних
" . 0
лучей, которая называется продольной сферической аберрацией.
* Математическое доказательство этого вывода см. в Приложении.

30 |
Тема 1. Геометрическая оптика |
|
|
!"#$% &%'(')#*
!"#. #.$). D?)&"2)#7'G ':)&&'3"G
Величина cс зависит от кривизны поверхностей, показателя преломления линзы и диаметра ее входного отверстия.
Для положительных (собирающих) линз cс < 0 (рис. 1.24), для отрицательных (рассеивающих) линз cс > 0. Комбинируя линзы разного знака, можно в значительной степени устранить сферическую аберрацию.
Хроматическая аберрация
Фокусное расстояние тонкой линзы определяется соотношением
(1.39):
! # |
1 |
# #n $ |
! |
1 |
$ |
1 |
" |
|
|
1% % |
& |
& ! |
|||||||
f ' |
(1 |
|
|||||||
|
|
( |
|
(2 ) |
|
||||
где n Ð относительный показатель преломления линзы; r1 и r2 Ð радиусы кривизны преломляющих поверхностей.
Так как показатель преломления вещества зависит от длины волны λ света (явление дисперсии), то и фокусное расстояние также является функцией λ. Для всех веществ наблюдается два вида дисперсии: нормальная (когда n убывает с ростом λ) и аномальная (когда n растет с ростом λ).
Для оптических стекол в видимой области спектра имеет место нормальная дисперсия, поэтому фокусное расстояние линз растет с увеличением λ.
На рис. 1.25 FФ и Fk Ð задние фокусы линзы для фиолетовых и красных лучей соответственно.
