
Основы механики твердого деформируемого тела
.pdf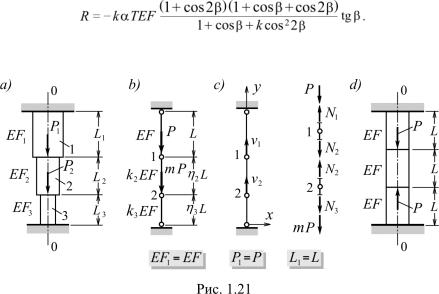
Глава 1 |
141 |
после чего по формуле (1.41b) вычисляется опорная реакция
При T > 0 стержни 1 и 2 растянуты, а стержень 3 сжат.
Нестандартно, но с сохранением стандартной технологии, может быть решена и следующая задача. На рис. 1.21a изображен трехступенчатый стержень заданных размеров, материала и при известном силовом воздействии. Требуется установить его напряженно-деформированное состояние. Конструкция симметрична относительно оси 0 − 0, поэтому точки, принадлежащие оси бруса, в горизонтальном направлении не перемещаются. Это позволяет представить расчетную модель системы так, как это показано на рис. 1.21b. Использование указанных на нем безразмерных параметров
η |
|
= |
L2 |
, η |
|
= |
|
L3 |
; k = |
EF2 |
, k = |
EF3 |
; m = |
P2 |
2 |
|
3 |
|
|
|
|
||||||||
|
|
L1 |
|
2 |
EF1 |
3 |
EF1 |
|
P1 |
|||||
|
|
|
|
|
|
L1 |
|
|
||||||
дает возможность сделать предстоящие выкладки более компактными. Состояние стержня характеризуют два перемещения v1 и v2, показанные на рис. 1.21c. Условия равновесия узлов 1 и 2 записываются, ввиду их очевидности, без комментариев:
N1 − N2 = P, N2 − N3 = mP. |
(1.44) |
Столь же очевидны кинематические и физические уравнения рассматриваемой задачи:
∆1 = −v1 |
, ∆2 = v1 − v2, ∆3 = v2, |
(1.45) |
∆1 = N1/J, ∆2 = η2N2 |
/k2J, ∆3 = η3N3/k3J, J = EF/L. |
(1.46) |
142 Часть II
Решение полной системы (1.44)–(1.46) в перемещениях строится обыч-
ным образом. Так как (i = 2, |
3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
N1 = J ∆1, N2 = µ2J ∆2, N3 = µ3J ∆3, µi = ki/ηi, |
|
(1.46a) |
||||||||||||||||||||||||
то (см. формулы (1.45)) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
N1 = −J v1, |
|
N2 = µ2J (v1 − v2), N3 = µ3J v2 |
(1.47) |
|||||||||||||||||||||||
и |
|
|
|
(1 + µ2)v1 − µ2v2 = −P/J, |
|
|
|
|
|
|
(1.44a) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
µ v |
+ (µ |
+ µ )v |
|
= |
|
mP/J. |
|
|
|
|
|
|
||||||||
|
|
|
|
− 2 |
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
||
Отсюда следует, что |
|
1 |
|
|
2 3 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
P (1 + m)µ + µ |
|
|
|
P (1 + m)µ |
+ m |
|||||||||||||||||||||
v1 = − |
|
|
|
|
|
|
2 3 |
, v2 = |
− |
|
|
|
|
|
|
|
2 |
. |
||||||||
J |
µ |
2 |
+ µ |
µ + µ |
J |
µ |
2 |
+ µ |
µ |
|
+ µ |
|||||||||||||||
|
|
|
|
|
|
2 |
|
3 |
3 |
|
|
|
|
|
|
|
|
|
2 |
|
3 |
3 |
|
|||
Подстановка этих величин в формулы (1.47) дает: |
|
|
|
|
|
|
|
|||||||||||||||||||
N1 = |
P [(1 + m)µ2 + µ3] |
, |
N2 |
= |
µ2P (m − µ3) |
, |
||||||||||||||||||||
|
µ2 + µ2µ3 + µ3 |
|||||||||||||||||||||||||
|
|
|
µ2 + µ2µ3 + µ3 |
|
|
|
|
|
|
|
||||||||||||||||
Пусть
k2 = k3 = η2 = η3 = 1, m = −1,
т. е. конструкция имеет вид, представленный на рис. 1.21d. Тогда (см. формулу (1.46a)4) µ2 = µ3 = 1 и
v1 = −v2 = − |
P L |
|
= N3 = |
P |
|
= − |
2P |
|
|
, N1 |
|
, N2 |
|
. |
|||
3EF |
3 |
3 |
||||||
Решение в силах требует составления одного условия совместности удлинений стержней. Такое условие может быть получено сложением равенств (1.45): ∆1 + ∆2 + ∆3 = 0. Дальнейшие вычисления выполняются достаточно просто. Надо при помощи формул (1.46) в только что записанном условии совместности интегральных деформаций заменить величины ∆i на усилия, добавить два уравнения равновесия (1.44) и решить образовавшуюся систему трех уравнений с тремя неизвестными.
1.12. Дисково-стержневые конструкции. Полная система уравнений дисково-стержневой конструкции состоит из условий равновесия, кинематических соотношений и закона Гука. При силовом воздействии последний записывается в форме (1.29), а если воздействие несиловое, то в форме
Глава 1 |
143 |
(1.29a) либо (1.38). Несложно составить и условия равновесия конструкции. Что же касается кинематических соотношений, то перед тем, как их составить, надо установить число степеней свободы диска, выбрать параметры, характеризующие его состояние, и выразить через них линейные перемещения uj , vj всех точек (узлов), в которых к диску присоединяются деформируемые стержни.
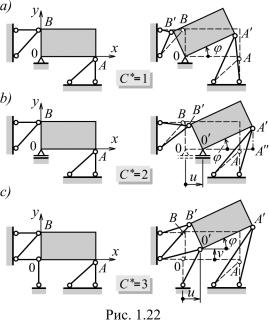
Конструкция, изображенная на рис. 1.22a, состоит из жесткого диска, прикрепленного к земле при помощи четырех податливых стержней, и неподвижной шарнирной опоры. При любом внешнем воздействии этот диск сможет лишь повернуться относительно точки 0 на некоторый угол ϕ, который и выбирается в качестве единственного параметра, который характеризует состояние конструкции. Стало быть, C = = 1. Угол ϕ мал, поэтому допустимо считать, что при повороте диска точка A не перемещается по горизонтали, а точка B – по вертикали.
На рис. 1.22b показана конструкция с подвижной шарнирной опорой 0. Внешнее воздействие на такую конструкцию приведет не только к повороту диска, но и к его горизонтальному смещению. Именно в виде суперпозиции двух перемещений, следующих одно за другим: линейного – на расстояние u вдоль оси 0x и поворотного – на угол ϕ относительно точки 0 , можно представить себе движение диска в целом. Таким образом, в данном случае C = 2 и параметрами состояния служат перемещения u и ϕ. Ввиду их малости можно считать, что точка B остается на горизонтали и AA = 00 = u. Случай C = 3 представлен на рис. 1.22c. После сказанного выше его можно не комментировать.
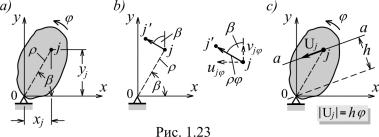
Изменение длин деформируемых стержней зависит от перемещений тех точек, в которых эти стержни присоединяются к диску (см. точки A и B на рис. 1.22). Надо уметь выражать перемещения uj , vj узловых точек через параметры u, v и ϕ. Очевидно,
uj = u + ujϕ, vj = v + vjϕ,
где ujϕ, vjϕ – доли горизонтальной и вертикальной составляющих переме-
144 |
Часть II |
щения узла j при повороте диска на угол ϕ. Пусть диск поворачивается относительно неподвижной точки 0 против часовой стрелки на малый угол ϕ (рис. 1.23a). В этом случае можно считать, что точка j перемещается по перпендикуляру к радиусу ρ вращения этой точки, причем ρ tg ϕ ≈ ρ ϕ.
По рис. 1.23b видно, что
ujϕ = −ρϕ sin β, vjϕ = ρϕ cos β,
а так как ρ sin β = yj , ρ cos β = xj , то
ujϕ = −yj ϕ, vjϕ = xj ϕ.
Таким образом, чтобы найти величину линейного перемещения Uj фиксированной точки j по заданному направлению a–a (см. рис. 1.23c), надо значение ϕ угла поворота диска, которому точка j принадлежит, умножить на расстояние h от центра вращения 0 до линии a–a. Этим правилом и следует руководствоваться при вычислениях.
Если перемещения uj и vj узла j известны и стержень i крепится одним концом к земле, а другим – к узлу j, то
∆i = −(uj li + vj mi), i = 1, 2, . . . , C, |
(1.48) |
что совпадает с равенством (1.28). В этой формуле C – число деформируемых стержней, li, mi – направляющие косинусы оси стержня i, начинающегося
вузле j.
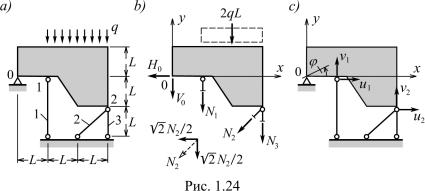
1.13.Система с одной степенью свободы. Рассматривается конструкция, изображенная на рис. 1.24a, при заданных генеральных размерах, осе-
вых жесткостях EFi деформируемых стержней и внешней нагрузке. Требу-
ется найти усилия Ni в стержнях 1–3, составляющие реакции шарнирной опоры 0, а также перемещения узлов 1 и 2. Конструкция статически неопределимая, поэтому нужно формировать полную систему уравнений.
Уравнения |
|
Px |
|
|
= 0, |
|
Py = 0, |
M0 |
= 0 равновесия диска (см. |
|||||||||
рис. 1.24b) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
имеют вид: |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
√ |
|
N2 |
|
|
|
√ |
|
N2 |
|
|
|||||
|
−H0 − |
2 |
= 0, |
|
2 |
|
− 2qL = 0, |
|||||||||||
|
|
|
|
|
|
−V0 − N1 − |
|
|
|
− N3 |
||||||||
|
|
|
|
2 |
|
|
2 |
|
||||||||||
Глава 1 |
|
|
|
|
|
145 |
|||
√ |
|
|
|
√ |
|
|
|
|
|
2 |
N2 · 3L − |
2 |
|
|
· L − N3 · 3L − 2qL · 2L = 0. |
||||
−N1 · L − |
|
|
|
|
N2 |
||||
2 |
2 |
||||||||
Первые два равенства определяют опорные реакции:
|
√ |
|
|
|
|
|
√ |
|
|
|
|
|
||
2 |
|
2 |
|
|
|
|||||||||
H0 = − |
|
|
N2 |
, |
V0 = −N1 − |
|
|
N2 − N3 |
− 2qL, |
(1.49) |
||||
2 |
|
2 |
||||||||||||
а третье – |
N1 + 2√ |
|
|
|
|
|
|
|
|
|||||
|
|
|
2 |
N2 + 3N3 = −4qL |
|
(1.50) |
||||||||
включается в полную систему уравнений в качестве статического уравнения. По рис. 1.24c видно (см. также рис. 1.23c), что
v1 = Lϕ, |
u1 = 0, |
v2 = 3Lϕ, u2 = Lϕ. |
|
|
|
|
||||||||||||||
Тогда в соответствии с формулой (1.48) |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
√ |
|
|
||
∆1 = v1 = Lϕ, ∆2 = u2 cos 45o + v2 cos 45o = |
2 |
Lϕ |
+ |
2 |
3Lϕ, |
|||||||||||||||
|
2 |
2 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
∆3 = v2 = 3Lϕ |
|
|
|
|
|
|
|
|
|
|
|
||||||
или |
|
|
∆2 = 2√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
∆1 = Lϕ, |
2 |
Lϕ, |
∆3 = 3Lϕ. |
|
|
|
(1.51) |
|||||||||||||
Физические уравнения состоят из трех соотношений закона Гука: |
||||||||||||||||||||
|
2N1L |
|
√ |
|
N2L |
|
|
|
|
|
|
|
|
|
||||||
∆1 = |
, ∆2 = |
2 |
∆3 = |
|
N3L |
|
|
|
(1.52) |
|||||||||||
|
|
|
, |
|
|
|
|
. |
|
|
||||||||||
EF1 |
|
|
|
|
|
|
|
|||||||||||||
|
|
EF2 |
|
|
|
EF3 |
|
|
|
|
||||||||||
Полная система уравнений (1.50) – (1.52) конструкции получена. Ее решение в перемещениях строится следующим образом. Из закона Гука (1.52)
исключаются интегральные деформации (1.51): |
|
N1 = EF1 ϕ/2, N2 = 2EF2 ϕ, N3 = 3EF3 ϕ. |
(1.53) |

146 |
|
|
|
|
Часть II |
Эти усилия подставляются в уравнение равновесия (1.50), что дает |
|
||||
ϕ = − |
EF1 + 8√ |
8ql |
|
||
|
EF2 + 18EF3 |
. |
|
||
2 |
|
||||
Усилия Ni и реакции H0, V0 определяются формулами (1.53) и (1.49). Задача
решена. В частности, при EF1 = EF2 = EF3 = EF и обозначении A = |
|||||||||||||||||||||
= (19 + 8√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2)/4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ϕ = − |
8qL |
|
= − |
qL |
|
N2 = − |
4qL |
N3 = − |
6qL |
||||||||||||
|
, N1 |
|
|
|
|
, |
|
, |
|
|
, |
||||||||||
AEF |
A |
A |
A |
||||||||||||||||||
|
|
|
|
|
2√ |
|
ql |
|
|
5 + 4√ |
|
|
|
|
|
||||||
|
|
|
|
H0 = |
2 |
|
= − |
2 |
|
|
|
||||||||||
|
|
|
|
|
, |
|
V0 |
|
|
ql. |
|||||||||||
|
|
|
|
A |
2A |
||||||||||||||||
Для решения задачи в силах из формул (1.51) надо исключить угол ϕ: |
|||||||||||||||||||||
|
|
|
|
∆2 = 2√ |
|
|
∆3 = 3∆1 |
|
|
|
|||||||||||
|
|
|
|
2∆1, |
|
|
|
||||||||||||||
и перейти тем самым к условиям совместности удлинений стержней. При помощи закона Гука (1.52) эти условия приводятся к виду:
N2 |
= |
|
4N1 |
, |
N3 |
= |
6N1 |
. |
(1.54) |
EF2 |
|
EF3 |
|
||||||
|
EF1 |
|
EF1 |
|
|||||
Остается решить систему трех уравнений (1.54) и (1.50) относительно усилий N1–N3. Результат будет таким же, что и при решении в перемещениях.
Пусть теперь в условия задачи вносится следующее изменение: помимо распределенной нагрузки интенсивности q конструкция испытывает и кинематическое воздействие, состоящее в постановке при ее монтаже укороченного на величину δ стержня 2. В этой новой задаче статическое уравнение (1.50) и кинематические соотношения (1.51) сохраняются, но в закон Гука (1.52) придется внести коррективы. Точнее, изменится только второе из
равенств (1.52) (см. также формулы (1.53)): |
|
|
|
|
|
|||||
|
√ |
|
N2L |
|
|
√ |
|
δ |
|
|
∆2 = |
2 |
− δ, N2 = EF2 |
2ϕ + |
2 |
. |
|||||
EF2 |
|
2L |
||||||||
В результате угол наклона диска увеличится по абсолютной величине:
= 8qL2 + 4EF2δ
ϕ −L(EF1 + 8√2EF2 + 18EF3) .
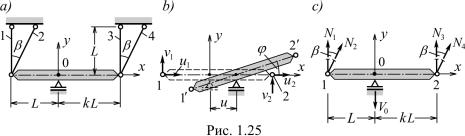
1.14. Система с двумя степенями свободы. Стержни 1–4 конструкции, изображенной на рис. 1.25a, испытывают повышение температуры на T oC.
Глава 1 |
147 |
Осевые жесткости стержней одинаковы, размеры стержней заданы. Требуется найти усилия в деформируемых стержнях, реакцию опоры 0 и перемещения узлов 0, 1, 2. По рис. 1.25b видно, что C = 2. В качестве параметров состояния выбираются линейное перемещение u диска по горизонтали и его поворотное перемещение ϕ относительно точки 0.
Условия равновесия конструкции составляются по рис. 1.25c:
Px = 0 : N2 sin β + N4 sin β = 0,
Py = 0 : N1 + N2 cos β + N3 + N4 cos β − V0 = 0,
M0 = 0 : N1L + (N2 cos β)L − N3kL − (N4 cos β)kL = 0.
Второе из этих условий приводится при помощи первого к виду:
V0 = N1 + N3. |
(1.55) |
Отсюда после определения усилий можно будет найти опорную реакцию V0. Два других условия равновесия
N2 + N4 = 0; |
N1 + N2 cos β − N3k − kN4 cos β = 0 |
(1.56) |
|
войдут в полную систему уравнений задачи. Согласно рис. |
1.25b, |
|
|
u1 = u, |
v1 = −ϕL, u2 = u, v2 = kϕL. |
|
|
Проецирование этих узловых перемещений на оси деформируемых стержней приводит к кинематическим уравнениям конструкции:
∆1 = ϕL, ∆2 = ϕL cos β − u sin β,
(1.57)
∆3 = −kϕL, ∆4 = −kϕ cos β − u sin β.
Физические уравнения составляются при помощи формулы (1.38):
∆1 |
= |
N1L |
|
+ αT L, ∆2 = |
N2L |
+ |
|
αT L |
, |
|
EF |
EF cos β |
cos β |
||||||||
|
|
|
|
|
||||||

148 |
|
|
|
|
|
|
|
|
|
Часть II |
∆3 = |
N3L |
+ αT L, ∆4 |
= |
|
N4L |
+ |
αT L |
|
||
|
EF cos β |
cos β |
||||||||
|
|
EF |
|
|
|
|||||
или (J = EF/L) |
|
|
|
|
|
|
|
|
|
|
N1 |
= J (∆1 − αT L), |
N2 |
= J (∆2 cos β − αT L), |
|||||||
|
= J (∆3 − αT L), |
|
|
|
|
|
(1.58) |
|||
N3 |
N4 |
= J (∆4 cos β − αT L). |
||||||||
При решении задачи в перемещениях из равенств (1.58) исключаются удлинения стержней ∆i. Для этого используются соотношения (1.57):
N1 = J L(ϕ − αT ), |
|
|
N2 = J (ϕL cos 2β − u sin β cos β − αT L), |
(1.59) |
||||||||||||||||||||||||||||||
N3 = −J L(kϕ+αT ), |
N4 = −J (kϕL cos 2β +u sin β cos β +αT L). |
|||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||
Остается подставить усилия (1.59) в уравнения равновесия (1.56): |
|
|||||||||||||||||||||||||||||||||
|
|
ϕL(1 − k) cos 2β − u sin 2β = 2αT L, |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
2 |
)(1+cos |
3 |
β) |
|
u(1 |
|
k) sin β cos |
2 |
β = αT L(1 |
|
|
|
k)(1+cos β) |
|
||||||||||||||||||||
ϕL(1+k |
|
− |
− |
|
− |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
и найти решение этой системы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
ϕ = |
|
|
2αT (1−k) |
|
, |
|
u = |
|
2αT L |
+ |
|
1−k |
ϕL. |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
2(1+k2) + (1+k)2 cos 3β |
|
|
|
|
|
−sin 2β |
|
2tgβ |
|
||||||||||||||||||||||||
При k = 1 решение упрощается: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
ϕ = 0, |
u = |
− |
2αT L |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
sin 2β |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
В этом случае (см. формулы (1.58) и (1.55)): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
N1 = N3 = −αT EF, |
|
N2 = N4 = 0, |
|
V0 = −2αT EF. |
|
|||||||||||||||||||||||||||||
При k = 2, β = 45o результаты решения задачи будут следующими: |
|
|||||||||||||||||||||||||||||||||
|
|
8B |
|
|
|
|
|
|
|
2(38 + 9√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
2)BL |
|
|
|
|
|
αT EF |
|
||||||||||||||||||
ϕ = − |
|
, u = |
− |
|
|
|
|
|
|
|
|
; |
|
B = |
40 + 9√ |
|
; |
|
|
|
||||||||||||||
EF |
|
|
EF |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|||||||||||||||||||||||||
N1 = −3(16 + 3√ |
|
|
|
N2 = −N4 = −6B, |
|
N3 = −3(8 + 3√ |
|
|
||||||||||||||||||||||||||
2)B, |
|
|
2)B. |
|||||||||||||||||||||||||||||||
Имеет смысл объяснить себе, почему именно такими получились знаки у перемещений и усилий.
Глава 1 |
149 |
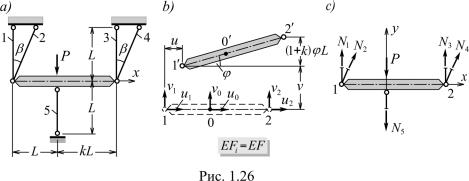
1.15. Система с тремя степенями свободы. Пусть теперь диск рассмотренной в предыдущем пункте конструкции опирается на деформируемый стержень и в точке 0, а внешнее воздействие является силовым (рис. 1.26a). Состояние такой конструкции описывается тремя параметрами – линейными перемещениями u, v диска и его поворотом на угол ϕ относительно узла 1 (см. рис. 1.26b). Требуется найти усилия в стержнях 1–5.
Условия Px = 0, Py = 0, M0 = 0 равновесия диска составляются при помощи рис. 1.26c:
N2 |
+ N4 |
= 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
N |
1 |
+ N |
3 |
+ (N |
2 |
+ N |
) cos β |
|
|
N |
5 |
= P, |
|
(1.60) |
|||
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N1L + N2L cos β |
− |
kLN3 |
− |
kLN4 cos β = 0, |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
а условия совместности перемещений узлов и изменений длин стержней – при помощи рис. 1.26b:
∆1 = −v1, ∆2 = −v1 cos β − u1 sin β, ∆3 = −v2,
∆4 = −v2 cos β − u2 sin β ∆5 = v0.
Так как u0 = u1 = u2 = u, v0 = v + Lϕ, v1 = v, v2 = v + (1 + k)Lϕ, то
∆1 = −v, ∆2 = −v cos β − u sin β, ∆3 = −v − (1 + k)Lϕ,
(1.61)
∆4 = −[v + (1 + k)Lϕ] cos β − u sin β, ∆5 = v + Lϕ.
Физические уравнения имеют обычный для силового воздействия вид:
∆i = |
NiL |
, i = 1, 3, 5; ∆j = |
Nj L |
, j = 2, 4. |
(1.62) |
||
EF |
|
EF cos β |
|||||
|
|
|
|
||||

150 |
Часть II |
Решение полной системы уравнений (1.60)–(1.62), как и обычно, проще строится в перемещениях, ибо разрешающая система содержит только три соотношения, а не пять, как это было бы при решении в силах. Из равенств (1.61) и (1.62) следует (J = EF/L):
N1 = −J v, N2 = −J (v cos β +u sin β) cos β, N3 = −J [v +(1+k)Lϕ],
|
EF |
(1.63) |
||
N4 = −J [v cos β + u sin β +ϕL(1+k) cos β] cos β, N5 = |
(v +Lϕ). |
|||
|
|
|||
L |
|
|||
Тогда (усилия (1.63) подставляются в условия равновесия (1.60)): |
||||
2v cos β + 2u sin β + Lϕ(1+k) cos β = 0, |
|
|||
|
|
|
||
|
|
|
||
− |
|
|
||
|
|
|||
3v + Lϕ(2+k) = P L/EF, |
|
|
||
|
|
|||
|
|
|
||
v(k−1)(1+cos 3β)+u(k−1) sin β cos 2β+
+Lϕk(1+k)(1+cos 3β) = 0.
Эту систему разрешающих уравнений можно решить, опираясь на правило Крамера:
v = − |
P |
|
[2k+(1+k) cos 3β], |
u = |
P |
(1+k)(1+cos |
3β) |
||||||
|
|
|
|
|
|
|
a, |
||||||
DJ |
DJ |
|
tg β |
|
|
||||||||
ϕL = |
2P (k−1) |
|
, D = |
4(1+k+k2)+3(1+k)2 cos 3β |
. |
||||||||
|
|
||||||||||||
|
|
|
DJ |
|
|
|
1+k |
|
|
|
|||
Подстановка этих величин в формулы (1.59) приводит к усилиям
N1 = |
P |
[2k+(1+k) cos 3β], |
N2 = −N4 = |
P |
(k−1) cos 2β, |
|
|||||
|
|
|
|||||||||
D |
D |
|
|||||||||
N3 = |
P |
[2+(1+k) cos 3β], N5 |
= − |
P 2(1+k2)+(1+k)2 cos 3β |
. |
||||||
D |
D |
|
|
|
1 + k |
||||||
(1.64)
Случаи k = 1 и k = 2, β = 45o можно проанализировать самостоятельно. При решении задачи в силах из равенств (1.61) исключаются перемеще-
ния. С этой целью из 1-го, 5-го и 2-го уравнений системы (1.61) последовательно находят величины v, Lϕ, u sin β:
v = −∆1, Lϕ = ∆5 − v = ∆5 + ∆1,
u sin β = −∆2 − v cos β = −∆2 + ∆1 cos β,
