10. УРАВНЕНИЯ МАКСВЕЛЛА

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Белорусский государственный университет информатики и радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

ыщо одна методичко по физице.pdf

Скачиваний:

273

Добавлен:

11.05.2015

Размер:

1.56 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 86 7 8 > Следующая >>>

находится в одной плоскости с П-образным проводником, вектор скорости

I			O		рамки v перпендикулярен проводнику.
I			O		4. В магнитном поле, создаваемом длинным
					4. В магнитном поле, создаваемом длинным
					прямым проводником с током I , находится
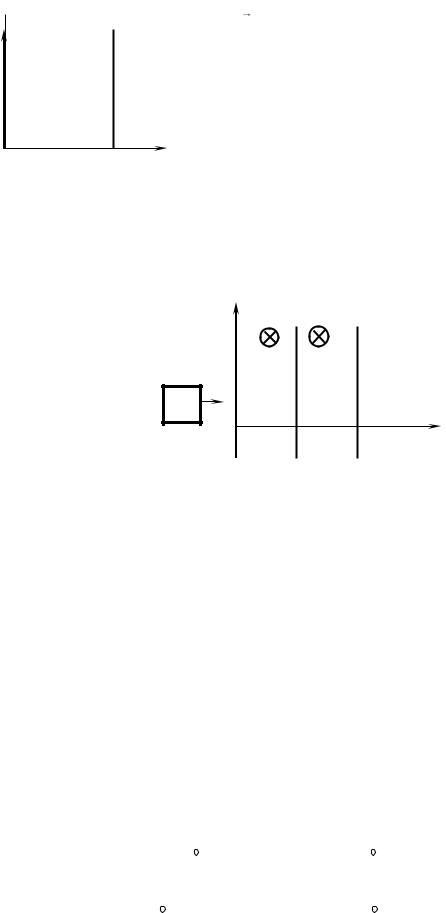
					квадратная рамка со стороной а. Рамку поворачивают
			O		вокруг оси ОО′ на 180o (рис. 50). Найти, какой заряд
					вокруг оси ОО′ на 180o (рис. 50). Найти, какой заряд
					протекает через поперечное сечение проводника
					протекает через поперечное сечение проводника
		b		X	рамки. Проводник находится в одной плоскости с
		b		X	рамкой, расстояние между проводником и осью ОО′
	Рис. 50				рамкой, расстояние между проводником и осью ОО′
	Рис. 50				равно b.
					равно b.
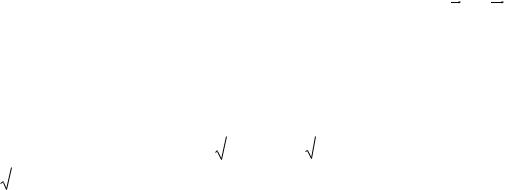
5.		Квадратная		рамка со стороной a перемещается в пространстве с

постоянной скоростью v в областях с различными значениями модуля вектора индукции магнитного поля (рис. 51). Построить график зависимости ЭДС индукции рамки от координаты ее левой стороны x.

B0 3B0

Рис. 51

В качестве вспомогательного замкнутого контура

по которому выполняется

ОСНОВНЫЕ ЗАКОНЫ И ФОРМУЛЫ

Уравнения Максвелла в дифференциальной форме:

		, B 0;
, E B ;		, B 0;

	t	; , D .
, H j D		; , D .

Эквивалентные им уравнения Максвелла в интегральной форме:


			B
	E, dl			t	, dS ;	B, dS 0;
	L		S		S

				D
							dV.
H , dl j				t	, dS ; D, dS
L		S			S		V

Величину D называют плотностью тока смещения. Для изотропных

сред в случае достаточно слабых и медленно меняющихся полей уравнения
Максвелла дополняются следующими материальными уравнениями:

D 0 E, B 0 H, j		E .
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача 1. Точечный заряд	q = 1,6 10 19	Кл движется равномерно и
		( v 106 м/с). Найти вектор
прямолинейно с нерелятивистской скоростью v

плотности тока смещения в точке P , находящейся на расстоянии r = 10 мкм от заряда на прямой, перпендикулярной его траектории и проходящей через заряд

(рис. 52).

Решение:

Плотность

тока

смещения

jсм

определяется

приращением

вектора

через

промежуток времени dt . Выражение для вектора D

в случае точечного заряда легко найти с помощью

теоремы Гаусса:

qer

4 r 2

где

– единичный вектор, определяющий

направление

радиус-вектора

точки

наблюдения P

v dt

относительно заряда.

За

промежуток

времени

заряд

совершит

Рис. 52

перемещение

dt . Приращение вектора смещения

равно

Модуль

приращения

определяется из подобия

dD D

треугольников (см. рис. 52):

dD vD dt vq dt .

4 r 3

Учитывая векторный характер величин и их направления, можем записать

j = 12,7 А/м 2 .

qv ,

см

4 r 3

Ответ:

qv , j

= 12,7 А/м 2 .

см

4 r 3

Задача 2. Плоский воздушный конденсатор, площадь каждой пластины которого S = 100 см 2 , включен последовательно в цепь переменного тока.

Найти максимальную плотность тока смещения в конденсаторе, если амплитуда синусоидального тока в подводящих проводах I0 = 1 мА.

Решение:

Сила тока в цепи меняется по закону I I0 cos t . Из определения силы тока I dq / dt получаем зависимость заряда на пластине конденсатора от времени:

sin t .

Связь между модулем вектора D и плотностью заряда пластины легко

найти с помощью теоремы Гаусса:

I0 sin t

где – поверхностная плотность заряда пластины конденсатора.

Отсюда находим модуль плотности тока смещения и его максимальное

значение.

см

I0 cos t

, j

см0

= 0,1 А/м 2 .

Ответ: j

см0

= 0,1 А/м 2 .

Задача 3. Пространство между обкладками плоского конденсатора, имеющими форму круглых дисков, заполнено однородной слабо проводящей средой с удельной проводимостью и диэлектрической проницаемостью . Расстояние между обкладками d . Пренебрегая краевыми эффектами, найти напряженность магнитного поля между обкладками на расстоянии r от их оси, если на конденсатор подано напряжение U U0 cos t .

Решение:

Проекции векторов напряженности электрического поля и смещения

между обкладками на ось конденсатора равны
E	U	U0 cos t	, D 0 E 0	U0 cos t	.
	d	d		d

Между обкладками возникают как ток проводимости, так и ток смещения, плотности которых равны

j E	U0 cos t	, jсм	D	0 sin t	.
	d		t	d

Эти токи порождают магнитное поле, напряженность которого можно вычислить, воспользовавшись уравнением Максвелла:

(H , dl )
	j	D , dS .
S		t

В качестве вспомогательного замкнутого контура L , по которому выполняется
интегрирование, выберем окружность радиусом			r , лежащую в плоскости,
перпендикулярной оси конденсатора с центром			на оси.	В силу симметрии
задачи напряженность магнитного поля		направлена		по касательной к
	H

выбранной окружности и постоянна по величине. Тогда последнее выражение можно переписать:

H 2 r ( j jсм ) r 2 .

Напряженность магнитного поля равна

H rU0 ( cos t 0 sin t) . 2d

Ответ: H rU0 ( cos t 0 sin t) . 2d

Задача 4. Ток, текущий по длинному прямому соленоиду, радиус сечения которого R = 5 см, меняют так, что магнитное поле внутри соленоида

возрастает со временем по закону B t 2 , где = 5 Тл/с 2 . Найти плотность

тока смещения как функцию расстояния r от оси соленоида. Вычислить плотность тока смещения при r = 2 см и t =4 с.

Решение:

Изменяющееся со временем магнитное поле порождает вихревое электрическое поле, напряженность которого вычислим воспользовавшись уравнением Максвелла:

интегрирование, выберем окружность радиусом r , лежащую в плоскости,

перпендикулярной оси соленоида с центром на оси. В силу симметрии задачи

напряженность электрического поля E направлена по касательной к выбранной окружности и постоянна по величине. Тогда последнее выражение можно переписать:

2 rE r 2 dBdt r 2 2 t, r R;

2 rE R2 dBdt R2 2 t, r R.

Знак минус определяет направление вектора E . В дальнейшем его учитывать не будем. Из полученных выражений находим E , D и jсм внутри и вне соленоида

E rt, D

rt, j

см

r, r R;

R2t

, D

R2t

, j

см

, r R.

Ответ: j

r, r R;

= 0,177 нА/м 2 .

см

, r R , j

см

Задача 5. По жесткому непроводящему тонкому круговому кольцу массой m равномерно распределен заряд q . Кольцо может свободно вращаться

вокруг оси, совпадающей с осью симметрии кольца. Вначале кольцо покоится,

а магнитное поле равно нулю. Затем включается однородное магнитное поле

B(t) , перпендикулярное плоскости кольца и произвольно меняющееся по

величине во времени. Найти зависимость от времени угловой скорости кольца.

Решение:

Изменяющееся со временем магнитное поле порождает вихревое электрическое поле, которое действует на заряды, распределенные по кольцу, приводя во вращение кольцо в замкнутом контуре, совпадающем с кольцом, возникает ЭДС индукции:

			B			dB
i	(E, dl )		t	, dS	= R2		,
i	(E, dl )			, dS	= R2	dt	,
		S				dt

где R – радиус кольца. Знак минус отражает правило Ленца.

За промежуток времени dt через произвольное поперечное сечение

контура пройдет заряд dq	q	dt . Работа ЭДС за этот промежуток времени
контура пройдет заряд dq	2	dt . Работа ЭДС за этот промежуток времени
	2
равна

dA dq R2		dB q		dt		q R2	dB	.
dA dq R2				dt				.
i		dt	2			2
		dt	2			2
Эта работа идет на приращение кинетической энергии кольца:
				mv 2
	dA dT d				.
	dA dT d				.

				2

Линейная скорость v R . Таким образом, получаем

m 2 R2		q R2
d			dB , или 2m d q dB .

	2	2

Интегрирование с учетом начальных условий дает выражение для угловой скорости:

		(t)	q		B(t) .
		(t)	2m		B(t) .
			2m
Выражение в векторном виде
			q
		(t)		B(t) .
		(t)	2m	B(t) .
	q
Ответ: (t)		B(t) .
Ответ: (t)	2m	B(t) .
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Точечный	заряд q = 1,6 10 19				Кл	движется	равномерно и
						( v 106 м/с).	Найти вектор
прямолинейно с нерелятивистской скоростью v						( v 106 м/с).	Найти вектор

плотности тока смещения в точке P , находящейся на расстоянии r = 10 мкм от заряда на прямой, совпадающей с его траекторией движения.

2. Определить величину напряженности магнитного поля в плоском

конденсаторе,	одна	из	пластин	которого удаляется	от неподвижной другой
пластины со скоростью
пластины со скоростью			v (v = 20 м/с), перпендикулярной пластинам. Разность
потенциалов	между	пластинами		U =20 кВ остается	постоянной. Начальное

расстояние между пластинами равно 0,5 м. Вычислить разность потенциалов в момент t = 0,1 с.

3. Длинный прямой соленоид имеет n витков на единицу длины. По нему течет переменный ток I I0 sin t , I0 = 8 А, = 300 рад/с. Найти плотность

тока смещения внутри соленоида как функцию расстояния r от оси соленоида. Радиус сечения соленоида равен 30 см. Вычислить амплитуду тока смещения при r = 10 см.

4. Плоский конденсатор образован двумя дисками, между которыми находится однородная слабопроводящая среда. Конденсатор зарядили и отключили от источника напряжения. Пренебрегая краевыми эффектами, определить магнитное поле внутри конденсатора в процессе разрядки

конденсатора.
5. В некоторой	области инерциальной системы	отсчета		имеется
вращающееся с угловой		модуль	индукции
вращающееся с угловой	скоростью магнитное поле,	модуль	индукции

которого равен B . Найти , E в этой области как функцию векторов			B и .

11. ЭЛЕКТРОМАГНИТЫЕ ВОЛНЫ.

ЭНЕРГИЯ И ИМПУЛЬС ЭЛЕКТРОМАГНИТНОГО ПОЛЯ

ОСНОВНЫЕ ЗАКОНЫ И ФОРМУЛЫ Уравнения Максвелла, записанные в однородной изотропной среде без

токов и зарядов:

, E B ,

, H D

( , B) 0, ( , D) ,

приводят к волновым уравнениям

2 E

E и 2 H

t 2

(здесь 2

– оператор Лапласа). Функции, которые являются

y 2

z 2

их решениями, представляют собой уравнения волн для векторов E и H . Таким образом, электрическое и магнитное поля, образуя единое

электромагнитное поле, могут существовать в отсутствие зарядов и токов в виде электромагнитных волн. Фазовая скорость их распространения, как

следует из волновых уравнений, равна
		v	1	c	,


			0 0
		3 108 м/с совпадает со скоростью распространения света в
где c 1/	0 0	3 108 м/с совпадает со скоростью распространения света в
вакууме.

Простейшим и одним из наиболее важных решений волнового уравнения

является решение в виде плоской волны:

		0 ) ,
E E0 cos( t kr	0 ), H H0 cos( t kr	0 ) ,

где k – волновой вектор, задающий направление распространения плоской электромагнитной волны. Модуль волнового вектора называется волновым числом. Оно определяется выражением

	k k		2 ,

			v
			v
где 2 v / –
где 2 v / –	длина волны. Векторы E, H и k				взаимно ортогональны и

образуют правовинтовую систему. Поворот				вектора		E	к вектору H дает

направление k .	Связав с направлениями			k , E, H		орты прямоугольной

декартовой системы координат i ,		j, k	соответственно,				можно получить для

ненулевых проекций векторов соотношение

P w .


	0 Ey		0 H z .
Оно выполняется в любой момент времени в любой точке пространства, а

также для амплитуд векторов. Векторы E, H		совершают колебания в одной фазе.

Электромагнитная волна, как и другие волны, переносит энергию. Плотность энергии электромагнитной волны равна сумме плотностей энергий электрического и магнитного полей:

w	E 2			H 2		EH
w	2				2	v .
	0				0
Плотность потока энергии

		S	E, H

называют вектором Пойнтинга. На практике измеряется интенсивность волны, которая равна модулю среднего по времени значения плотности потока энергии

				E 2
I S	0	/	0	E 2	/ 2 .
	0		0	0

Наряду с энергией электромагнитная волна обладает импульсом.

Плотность импульса электромагнитной волны в вакууме дается выражением
	E, H

p	c2	.
	c2

При поглощении телом падающая на его поверхность электромагнитная волна передает телу импульс. В соответствии со вторым законом Ньютона на тело со стороны волны действует сила, равная скорости изменения импульса тела. Если волна падает перпендикулярно поверхности тела и происходит полное поглощение волны, то давление на поверхность тела равно

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача 1. Плоская электромагнитная волна падает нормально на поверхность плоскопараллельного слоя толщиной l = 2 м из немагнитного вещества, диэлектрическая проницаемость которого экспоненциально падает от значения 1 = 4 на передней поверхности до 2 =2,25 – на задней. Найти время

распространения данной фазы волны через этот слой.

Решение:

Для немагнитной среды 1. Тогда скорость распространения волны

равна v c / 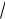. Перпендикулярно поверхности слоя проводим ось OX , начало

которой совмещаем с границей слоя, на которую падает волна. Тогда зависимость диэлектрической проницаемости от координаты x будет даваться выражением

1e kx ,

где коэффициент k определяется из условия 2 1e kl .

Разобьем слой на тонкие слои, границы которых определяются координатами x и x dx . Время прохождения такого слоя

e kx / 2 dx .

Время распространения фазы волны через весь слой равно

kx / 2

2l( 1

2 )

= 11,6 нс.

c ln(

)

Ответ:

2l( 1

2 )

= 11,6 нс.

c ln(

)

Задача 2. В вакууме распространяется плоская электромагнитная волна,

которая описывается уравнениями

E0 cos( t kr ), H H0 cos( t kr ) .

Исходя из уравнений Максвелла, выразить через заданные векторы

. Для E = 160 В/м и k = 0,5 м 1

вектор H

вычислить H

Решение:

Поля зависят только от фазы t kx x ky y kz z . Поэтому частные

производные полевых величин по координатам можно представить следующим образом:

x d

d y

d z

Воспользуемся уравнением Максвелла:

, E B

где B 0 H .

Подставим в уравнение заданные выражения для полей. Ротор напряженности электрического поля вычислим через определитель, воспользовавшись его свойствами. В результате получим



		ex			ey
		kx			k y
0 H0 ( )sin( t kr )
		E0x		E0 y

В вакууме	kc k /		0 0 .
окончательный результат:



ez	d cos
kz			k , E0 sin( t kr ) .
kz	d		k , E0 sin( t kr ) .
E0z	d
E0z
Подстановка		этого		выражения дает

										k , E , H
			H			0	/ 0			k , E , H						0 E =0,42 А/м.

				0							0		0
				0							0		0				0
						k										0
					k , E . H
Ответ:	H		0	/ 0	k , E . H							0 E			=0,42 А/м.

		0						0	0					0
		0	k					0	0			0		0
			k									0

Задача		3.	Плоская				электромагнитная волна											E E0 cos( t kx) ,

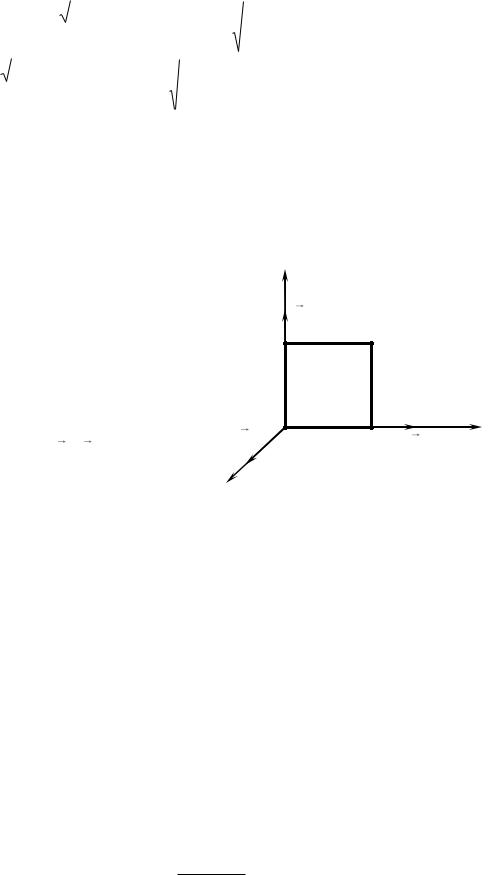
распространяющаяся в вакууме, наводит ЭДС индукции в квадратном контуре со стороной l (рис. 53). Найти зависимость от времени ЭДС индукции в

контуре по заданным E0 = 20 мВ/м, = 2 108

Решение:

Для вычисления ЭДС с учетом ее направления выберем обход контура по часовой стрелке. На участке контура 1–2 во

всех		точках		напряженность		поля
		cos t ,
E E		cos t ,	а	на	участке	3–4
	0
E E0 cos( t kl).				С учетом определения

ЭДС на некотором участке:

i (E, dl ) ,

рад/с, l = 1,5 м.

2 3

1 4

H0 O

l k

		a
получаем			Z
i	E0l cos t , i	E0l cos( t l / c) .	Рис. 53
i	E0l cos t , i	E0l cos( t l / c) .

	На участках	2–3 и 4–1 ЭДС равна нулю, так как вектор E

перпендикулярен отрезкам, задающим эти участки. Сложив ЭДС на всех участках, получаем ЭДС в контуре:

i E0l(cos t cos( t l / c)) = 60 cos t мВ.

Ответ: i E0l(cos t cos( t l / c)) = 60 cos t мВ.

Задача 4. Плоский воздушный конденсатор, обкладки которого имеют форму дисков радиусом R = 8 см, подключен к переменному синусоидальному напряжению частоты = 2000 рад/с. Найти отношение амплитудных значений магнитной и электрической энергий внутри конденсатора.

Решение:

В соответствии с условием задачи напряжение на конденсаторе меняется по закону U U0 sin t . Проекция напряженности электрического поля на

направление OX , перпендикулярное обкладкам конденсатора, равна

Ex U0 sin t , b

где b – расстояние между обкладками конденсатора.

Изменяющееся со временем электрическое поле приводит к появлению тока смещения, плотность которого равна

j		Dx	Ex	0U0 cos t .
см		t	0 t	b

Ток смещения приводит к возникновению магнитного поля в пространстве

между обкладками конденсатора. Для определения напряженности магнитного

поля воспользуемся теоремой о циркуляции вектора H :

(H , dl ) dtd S ( jсм , dS ).

В качестве замкнутого контура выберем окружность радиусом r R ,

лежащую в плоскости, параллельной обкладкам конденсатора. Центр окружности лежит на оси симметрии конденсатора. Тогда по теореме о циркуляции получаем

H 2 r jсм r	2	H	0U0 r cos t	.
			2b

Для вычисления энергии магнитного поля разбиваем объем между пластинами конденсатора на коаксиальные с осью симметрии конденсатора цилиндрические слои толщиной dr и внутренним радиусом r . Область изменения r : 0 r R . Энергия магнитного поля равна

Wм wм			R			H 2					R		2U 2 2r 2 cos2 t
Wм wм		dV			0	b 2 r dr						0	0 0			b 2 r dr
	V		0			2					0		2 4b2
	V		0								0
	2 U 2 2 R4 cos2						t			.
	0	0	0							.
	0	0	0
			16b

Энергия электрического поля в силу однородности поля E в
пространстве между обкладками равна
		W w V							E		2		U 2 R2 sin2	t	.
		W w V						0			b R2		0 0		.
			э	э				2					2b
								2					2b

Подставив максимальные значения энергий, получим искомое отношение:

Wм max

0 0R2 2

= 3,6 10 14 .

Wэ max

Ответ:

Wм max

0 0R2 2

3,6 10 14 .

Wэ max

Задача 5. Сила тока в очень длинном

соленоиде радиусом

R =10 см медленно

увеличивается от 0 до

I0 = 20 А. Число

витков

соленоида

на

единицу

длины

равно n

= 1000 м

. Найти количество

энергии, протекающей через замкнутый

коаксиальный с соленоидом

цилиндр

Рис. 54

длиной l = 0,5 м и радиусом основания r 5 см за полное время возрастания

тока (рис. 54). Сравнить полученное выражение с энергией магнитного поля внутри выделенного цилиндра.

Решение:

Напряженность магнитного поля в соленоиде параллельна его оси симметрии. Ее модуль равен

H nI .

Изменение со временем силы тока приводит к изменению со временем напряженности магнитного поля. В свою очередь это вызывает появление вихревого электрического поля, напряженность которого можно вычислить с помощью теоремы о циркуляции. В качестве замкнутого контура выберем окружность на поверхности указанного в условии задачи цилиндра. Тогда

	d					dI
(E, dl )		(B, dS )	E 2 r 0n				r2 .
(E, dl )	dt	(B, dS )	E 2 r 0n			dt	r2 .
		S
Напряженность электрического поля определятся выражением
		E	0nr dI		.
		E	2	dt	.
			2	dt
Знак минус указывает на то, что напряженность E направлена по касательной к

окружности в соответствии с правилом левого винта. Векторы E и								H взаимно
ортогональны. Плотность потока энергии – вектор Пойнтинга:

		S E, H .

Во всех точках замкнутого цилиндра вектор S перпендикулярен оси цилиндра и направлен к ней. Поэтому поток энергии через основания цилиндра будет равен нулю. Модуль вектора Пойнтинга равен

S EH 0n2rI dI . 2 dt

Поток энергии, поступающий в цилиндр, равен произведению модуля вектора Пойнтинга на площадь боковой поверхности цилиндра l2 r . За промежуток времени от 0 до t в цилиндр поступит количество энергии, равное

t		n2rI dI								I 0		n2r 2lI 2
W	0				2 rl dt 0n					2r 2l I dI	0	0 .
W		2		dt	2 rl dt 0n					2r 2l I dI		0 .
0		2		dt						0		2
0										0
Энергия магнитного поля внутри цилиндра равна
W w			V				H 2	r 2l		n2r 2lI 2
W w			V			0		r 2l	0	0 W = 0,49 Дж.
м		м					2			2
							2			2

Энергия, поступившая в цилиндр через его поверхность, равна энергии созданного внутри цилиндра магнитного поля.

<<< < Предыдущая 1 2 3 4 56 / 86 7 8 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
24.09.2019232.36 Кб22шпоры_MO.docx
#
17.09.20191.9 Mб5шпоры_все.docx
#
26.09.2019114.84 Кб1ШПОРЫ_ЭКОНОМ.docx
#
23.09.2019659.46 Кб2Шпоры_эпр.doc
#
15.11.20198.98 Mб18Шупейко-ТиП-практ.2 .docx
#
11.05.20151.56 Mб273ыщо одна методичко по физице.pdf
#
11.05.20151.48 Mб11Э.1Б.doc
#
11.05.20151.43 Mб8Э.1Б.doc
#
11.05.20151.7 Mб10Э.2В - МЕТОДИЧКА.doc
#
11.05.20152.56 Mб9Э.4Б.doc
#
25.11.2018583.17 Кб17Экзамен БДиСУБД.doc