1432-TEC

150

4) по найденным выражениям i(t), u(t) вычислить значения i(0), u(0) и убедиться в

правильности результата; 5) используя операторный метод расчета ПП, определить закон изменения тех же

i(t), u(t) , что и в п.3;

6)построить кривые изменения всех токов и напряжений, указав на графиках соответствующие докоммутационные значения;

7)записать алгоритм определения всех остальных токов и напряжений;

8)вычислить время переходного процесса для найденного переходного тока или напряжения;

9)сделать заключение (с соответствующим пояснением) о возможности рассматривать

вопределенном масштабе полученный i(t), u(t) в качестве соответствующей

переходной характеристики цепи; 10) сформулировать общие выводы по работе.

0.

Рисунок 10.6 Схемы электрических цепей

Варианты задания источника сигнала e(t):

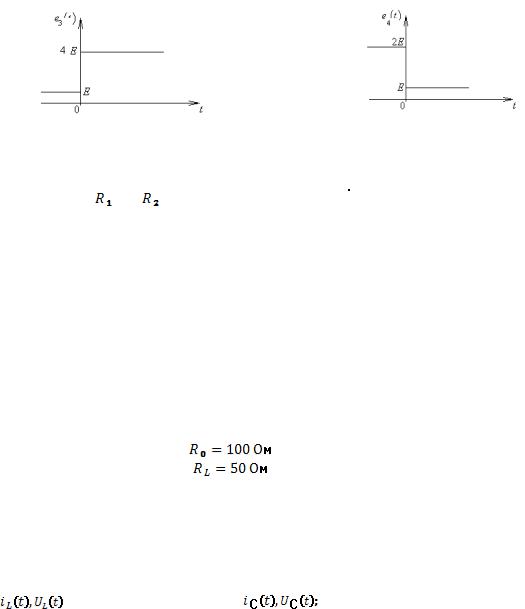
152

11. ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ ЦЕПЕЙ И ИХ СВЯЗЬ С ЧАСТОТНЫМИ

11.1 Цель занятия

Усвоить определения и смысл переходной и импульсной характеристик, их связь с частотными характеристиками. Научится по одной из характеристик цепи, находить другие характеристики этой же цепи.

11.2 Краткие теоретические сведения

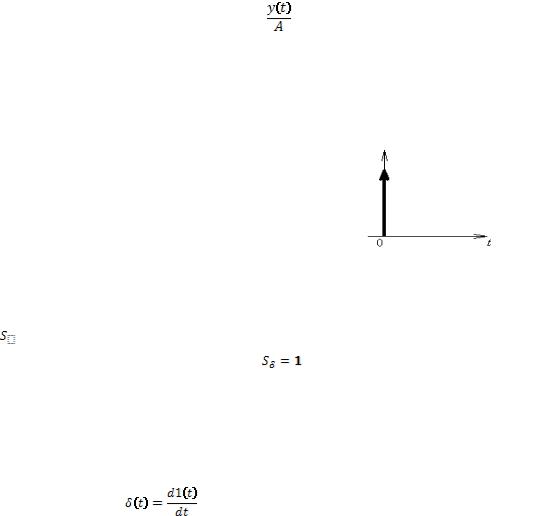
Переходная характеристика h(t) численно совпадает с реакцией y(t) линейной цепи с нулевыми НУ на действие функции Хэвисайда (функции включения, единичного скачка). Если воздействие равно А•1(t),

.

Рисунок 11.1 то переходная характеристика имеет вид:

Характеристика h(t) отражает закон изменения переходного напряжения (или тока) при подключении постоянного напряжения к линейной цепи с нулевыми НУ

Импульсная характеристика g(t) численно совпадает с реакцией y(t) линейной цепи с нулевыми НУ на действие δ(t).

после «электрического толчка», т.е характер свободных процессов после кратковременного поступле-

ния энергии в электрическую цепь. Следовательно, g(t)→0 при t→∞ для всех устойчивых цепей.

Т.к воздействия цепи (функция Хэвисайда и δ- функция) связаны между собой

воздействие связаны таким же образом во всей временной области :

154

Рисунок 11.5

Указания:

1)при переходе от К(ω)→h(t) и от h(t)→К(ω) использовать предельные соотношения;

2)при переходе от h(t)→g(t) использовать «графическое дифференцирование, смысл производной; обратить внимание на знак («+», если функция растет, «-» если убывает).

Типичная ошибка – утеря δ(t) в составе g(t) или утеря коэффициента перед δ(t): в задаче

2 –

п(е) 0.2 (е) h (t) ;

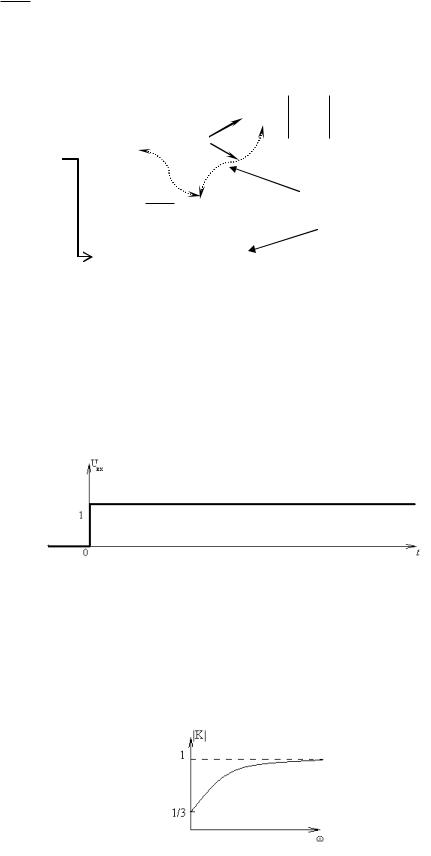
3) при построении схем с единственным реактивным эле - ментом, как в задачах 1 и 2, использовать «базовые» варианты Г-образных схем:

К=1:

К=0:

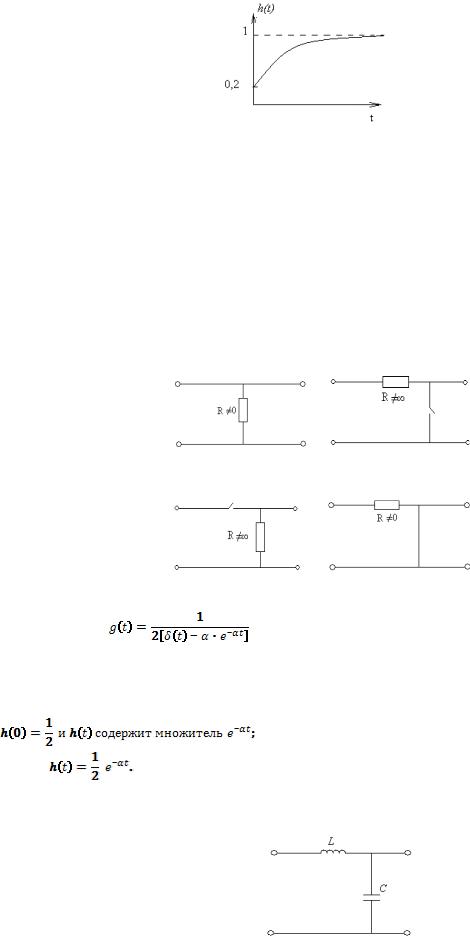
Задача 4. Для схемы без потерь, представленной на рисунке 11.6:

Рисунок 11.6

155

1)изобразить график К(ω) и φк(ω) на основе анализа схемы;

2)получить выражение К(р), ввести типовые обозначения LC1 p2 ;

3)получить выражения g(t) и h(t) и изобразить их графически.

Указание. K(p)→G(p)→g(t) K(p)→H(p)→h(t)

Задача 5. Для схемы с потерями обсудить изменения в характеристиках К(ω), h(t), g(t), полученных при решении задачи 4 для схемы без потерь.

11.4 Знания и умения

Знать:

1)характер входных воздействий при определении АЧХ, ФЧХ, h(t), g(t);

2)определение и что конкретно отражает каждая из времен-

ных характеристик;

3)«смысл» предельных соотношений;

4)связь временных характеристик между собой и обоснование этой связи;

5)связь частных и временных характеристик;

Уметь:

1)по одной из характеристик К(ω), h(t) или g(t), изобразить две другие;

2)на основе выражения К(р) находить изображения времен-

ных характеристик G(p) и H(p) и переходить к их оригиналам g(t) и h(t).

11.5 Формы контроля

Тестовый опрос.

11.6 Рекомендуемая литература

1. Попов В.П. Основы теории цепей.-М.: Высш. школа, 2007.-574 c.