
- •Раздел 6. Элементы векторной алгебры
- •6.1. Векторы и скаляры
- •6.2. Линейные операции над векторами
- •Свойства умножения.
- •6.3. Коллинеарные векторы
- •6.4. Компланарные векторы
- •6.5. Ориентация трех некомпланарных векторов в пространстве.
- •6.6. Проекция вектора на ось.
- •6.7. Прямоугольные декартовые координаты в пространстве.
- •6.8. Расстояние между двумя точками в пространстве
- •6.9 Действия над векторами в координатной форме
- •6.10 Скалярное произведение векторов
- •6.11. Векторное произведение.
- •6.12. Смешанное произведение.
6.8. Расстояние между двумя точками в пространстве

Пусть
![]() ‑ начальная точка отрезка
‑ начальная точка отрезка![]() и
и![]() ‑ конечная точка. Тоски
‑ конечная точка. Тоски![]() и
и![]() можно задать радиус-векторами
можно задать радиус-векторами![]() и
и![]() ,
где
,
где![]() и
и![]() .
Из треугольника
.
Из треугольника![]() следует, что
следует, что![]() .
Проектируя это векторное равенство на
оси координат и учитывая свойства
проекций, получим:
.
Проектируя это векторное равенство на
оси координат и учитывая свойства
проекций, получим:
![]() ,
,![]() ,
,![]() .
.
Из формулы
![]() получимрасстояние между двумя
точками
получимрасстояние между двумя
точками![]() и
и![]() :
:
![]() .
.
Пример. Ракета из пункта![]() прямолинейно переместилась в пункт
прямолинейно переместилась в пункт![]() .
Найти путь
.
Найти путь![]() ,
пройденный ракетой.
,
пройденный ракетой.
Решение.![]() .
Если найти направляющие косинусы вектора
перемещения
.
Если найти направляющие косинусы вектора
перемещения![]() ,
нетрудно определить направление движения
ракеты.
,
нетрудно определить направление движения
ракеты.
6.9 Действия над векторами в координатной форме

Пусть вектор
![]() задан проекциями на оси
задан проекциями на оси![]() ,
,![]() ,
,![]() .
Введём (орты) единичные векторы
.
Введём (орты) единичные векторы![]() ,
,![]() ,
,![]() ,
направленные по осям координат, и
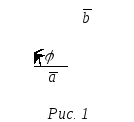
построим параллепипед (рис.1), диагональю
которого является вектор
,
направленные по осям координат, и
построим параллепипед (рис.1), диагональю
которого является вектор![]() ,
тогда вектора
,
тогда вектора![]() ,
,![]() ,
,![]() будуткомпонентамивектора
будуткомпонентамивектора![]() относительно осей
относительно осей![]() ,
,![]() ,
,![]() и
и
![]() ,
,![]() ,
,![]() .
.
Подставим эти выражения в равенство
![]() ,
,
в результате получили координатную формулу вектора
![]() .
.
Линейные операции над векторамитеперь можно записать в координатной форме.
Если
![]() и
и![]() ,
то
,
то
1)
![]() ,
,
т.е.
![]() или
или![]() ,
,
при сложении (или вычитании) векторов их одноименные координаты складываются (вычитаются);
2)
![]() ,
,
т.е.
![]() и
и![]() ,
,
при умножении вектора на скаляр координаты вектора умножаются на этот скаляр.
6.10 Скалярное произведение векторов
Определение 1.Подскалярным
произведением двух векторов![]() и
и![]() понимаетсячисло, равное
произведению длин этих векторов на
косинус угла между ними, т.е.
понимаетсячисло, равное
произведению длин этих векторов на
косинус угла между ними, т.е.
![]() ,
,
где
![]() .
.
Так как
![]() и
и![]() (рис.1), то скалярное произведение можно
записать в виде
(рис.1), то скалярное произведение можно
записать в виде
![]() .
.
Определение 2.Два вектора![]() и
и![]() называются ортогональными, если угол
между ними равен
называются ортогональными, если угол
между ними равен![]() .
Ортогональность векторов
.
Ортогональность векторов![]() и
и![]() обозначается
обозначается![]() .
.
Теорема (геометрическое свойство
скалярного произведения).![]() тогда и только тогда, когда
тогда и только тогда, когда![]() .
.
Доказательство.Необходимость.Пусть![]() ,
тогда
,
тогда![]() .
.
Достаточность.Если![]() ,
то
,
то![]() .
Возможны три случая:
.
Возможны три случая:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() .
.
Из этих случаев следует, что
![]() .□
.□
Алгебраические свойства скалярного произведения.
1.
![]() .
.
2.
![]() .
.
3.
![]() .
.
4.
![]() .
.
Скалярное произведение в координатах.
Теорема.Если![]() ,
,![]() ,
то
,
то
![]() .
.
Доказательство.Так как![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
то
,
то
![]()
![]()
![]() .□
.□
Так как
![]() и
и![]() ,
то из теоремы вытекает, что
,
то из теоремы вытекает, что
![]() .
.
6.11. Векторное произведение.
Определение. Векторным
произведениемвектора![]() на вектор
на вектор![]() называетсявектор
называетсявектор![]() ,
если:
,
если:
1)
![]() ;
;
2)
![]() и
и![]() ;
;
3) векторы
![]() образуют правую тройку.
образуют правую тройку.
Геометрические свойства векторного произведения.
Свойство 1.Необходимым и
достаточным условием коллинеарности
двух векторов![]() и
и![]() является равенство их векторного
произведения, т.е.
является равенство их векторного
произведения, т.е.![]() .
.
Доказательство.Необходимость.Пусть![]() ,
,![]() ,
,![]() ,
тогда
,
тогда![]() .
Следовательно,
.
Следовательно,![]() и
и![]() ,
поэтому
,
поэтому![]() ,
т.е.
,
т.е.![]() и
и![]() коллинеарны.
коллинеарны.
Достаточность. Пусть![]() и
и![]() коллинеарны,
тогда
коллинеарны,
тогда![]() и
и![]() или
или![]() .
Поэтому
.
Поэтому![]() и
и![]() .
Так как только нулевой вектор имеет
нулевую длину, то
.
Так как только нулевой вектор имеет
нулевую длину, то![]() .□
.□
Свойство 2.Абсолютная величина
векторного произведения равна площади
параллелограмма, образованного этими
векторами, т.е.![]() .
.
Доказательство. ![]() .□
.□

Алгебраические свойства векторного произведения.
1. ![]() (антиперестановочность).
(антиперестановочность).
2. ![]() (линейность).
(линейность).
3.
![]() .
.
4.
![]() .
.
Векторное произведение через координаты.
Теорема.Если в правой системе
координат![]() ,
,![]() ,
то
,
то
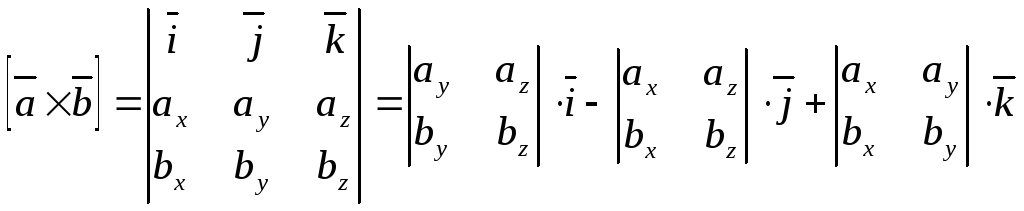 .
.
Доказательство.
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
 .□
.□
6.12. Смешанное произведение.
Определение.Смешанным
произведениемтрёх векторов![]() называетсячисло:
называетсячисло:
![]() ,
,
т.е. скалярное произведение векторов
![]() и
и![]() .
.
Свойства смешанного произведения.
Свойство 1.Если![]() компланарные, то
компланарные, то![]() .
.
Доказательство.Пусть![]() компланарные. Запишем смешанное
произведение этих векторов:
компланарные. Запишем смешанное
произведение этих векторов:

![]() .
.
Рассмотрим случаи:
1. Если один из векторов нулевой,
то![]() .
.
2. Если![]() ,
,![]() ,
,![]() и вектора
и вектора![]() и
и![]() ‑ коллинеарные, то
‑ коллинеарные, то![]() и, следовательно,
и, следовательно,![]() .
.
3. Пусть![]() ,
,![]() ,
,![]() и вектора
и вектора![]() и
и![]() ‑ неколлинеарные. Тогда из того, что
вектор
‑ неколлинеарные. Тогда из того, что
вектор![]() лежит в одной плоскости с векторами
лежит в одной плоскости с векторами![]() и
и![]() ,
а вектор
,
а вектор![]() перпендикулярен этой плоскости, вытекает,
что векторы
перпендикулярен этой плоскости, вытекает,
что векторы![]() и
и![]() ‑ перпендикулярные (т.е.
‑ перпендикулярные (т.е.![]() ),
поэтому
),
поэтому
![]() и
и![]() .□
.□
Свойство 2.Если![]() некомпланарные, то приведя их к общему
началу и построив на них параллепипед
объема
некомпланарные, то приведя их к общему
началу и построив на них параллепипед
объема![]() ,
получим
,
получим![]() ,
где
,
где
Доказательство.Из определения и свойств векторного произведения имеем:
![]() ,
,
где
![]() ‑ единичный вектор, такой, что
‑ единичный вектор, такой, что![]() ,
,![]() и тройка
и тройка![]() ,
а
,
а![]() ‑ площадь параллелограмма, построенного
на векторах
‑ площадь параллелограмма, построенного
на векторах![]() и
и![]() .
.
![]() .
.
Рассмотрим два случая.
1.Тройка![]() ‑ правая (рис.1), тогда угол
‑ правая (рис.1), тогда угол![]() ‑ острый, т.е.
‑ острый, т.е.![]() ,
и
,
и![]() .
Если
.
Если![]() ‑ высота параллепипеда, построенного
на векторах
‑ высота параллепипеда, построенного
на векторах![]() ,
то в этом случае
,
то в этом случае![]() и
и![]() .
.

2.Тройка![]() ‑ левая (рис.2), тогда угол
‑ левая (рис.2), тогда угол![]() ‑ тупой, т.е.
‑ тупой, т.е.![]() ,
и
,
и![]() .
В этом случае
.
В этом случае![]() и
и![]() .
.

Из рассмотренных случаев следует, что
![]() ,
где
,
где □
□
Свойство 3.Смешанное произведение не меняется при циклической перестановке, т.е.
![]() .
.
Доказательство.Пусть![]() ‑ некомпланарные.
‑ некомпланарные.
Докажем, что
![]() .
.
По свойству 2,
![]() и
и![]() .
Так как циклическая перестановка не
меняет ориентацию тройки, то
.
Так как циклическая перестановка не
меняет ориентацию тройки, то![]() и
и![]() .
.
Равенство
![]() доказывается аналогично.□
доказывается аналогично.□
Свойство 4.При перестановке
двух соседних множителей, смешанное
произведение меняет знак, т.е.![]() .
.
Доказательство.Пусть![]() ‑ некомпланарные. Докажем, что
‑ некомпланарные. Докажем, что![]() .
По свойству 2,
.
По свойству 2,![]() и
и![]() .
Так как нециклическая перестановка
меняет ориентацию тройки, то
.
Так как нециклическая перестановка
меняет ориентацию тройки, то![]() и
и![]() .□
.□
Свойство 5.![]() .
.
Доказательство.Из свойства
скалярного произведения следует, что![]() .
Поэтому надо доказать, что
.
Поэтому надо доказать, что![]() .
Так как перестановка циклическая, то
по свойству 3 это равенство выполняется.□
.
Так как перестановка циклическая, то
по свойству 3 это равенство выполняется.□
Смешанное произведение в координатах.
Теорема.Если в правой системе
координат![]() ,
,![]() ,
,![]() ,
то
,
то
 .
.
Доказательство.По свойству 5,![]() .
Так как
.
Так как
 ,
,
то
 .□
.□
