Урок 80 Анализ результатов контрольной работы

Цели:обобщить и систематизировать знания учащихся; проанализировать ошибки, сделанные в контрольной работе.

Ход урока

I. Анализ результатов контрольной работы.

Самые распространенные ошибки разбираются на доске с обсуждением, а затем каждый из учащихся делает работу над своими ошибками под контролем учителя.

II. Обобщение и систематизация знаний.

Те учащиеся, которые допустили ошибки в контрольной работе, после их исправления решают номера из учебника: № 754 (а, в); № 761;№ 778 (а, в);№ 786.

Сильным учащимся можно предложить задания повышенного уровня сложности.

1. № 774.

Решение:

а) Запишем числа ив виде многочлена:

Найдем их сумму и преобразуем её:

Очевидно, что число 11 (a+b) делится наa+b.

б)

Очевидно, что это число кратно 9.

2. № 760.

Решение:

Рассмотрим процесс движения мотоциклистов до их встречи. Пусть скорость первого мотоциклиста хкм/ч, тогда скорость второго 1,5хкм/ч. До встречи они вместе проедут расстояние, равное 240 км.

Заполним таблицу:

	s	υ	t
Первый мотоциклист	2,4хкм	хкм/ч	2,4 ч
Второй мотоциклист	2,4 · 1,5хкм	1,5хкм/ч	2,4 ч

Составим и решим уравнение:

2,4х+ 2,4 · 1,5х= 240;

2,4 (х+ 1,5х) = 240;

2,5х= 100;

х= 40.

Получаем, что скорости мотоциклистов равны 40 км/ч и 40 · 1,5 = = 60 км/ч.

Расстояние от пункта Адо места встречи равно 2,4х= 2,4 · 40 = 96 км. Тогда расстояние от места встречи доВравно 120 – 96 = 24 км.

Ответ: 40 км/ч, 60 км/ч, 24 км.

3. № 766.

Решение:

Сделаем рисунок к задаче:

Пусть в растворе первоначально было хг соли, значит, её концентрация была равна· 100 %. В новом растворе стало (х+ 20) г соли, то есть её концентрация стала равна· 100 %.

По условию концентрация соли повысилась на 3,75 %. Составим и решим уравнение:

· 100 –· 100 = 3,75;

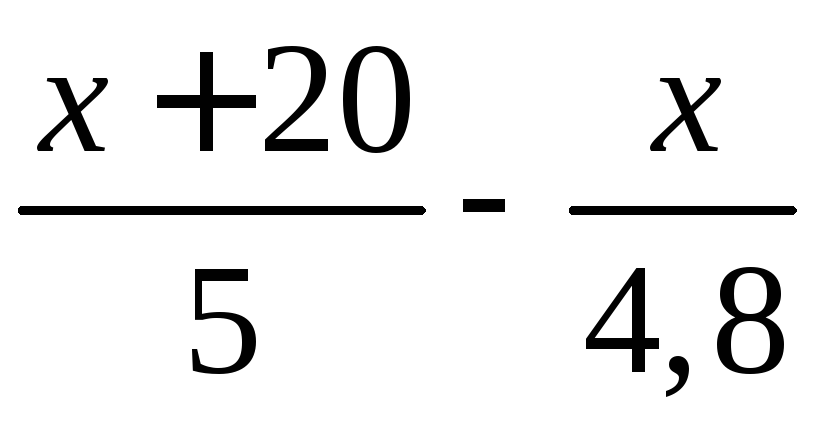= 3,75;

.

Домножим обе части уравнения на 120.

24 (х+ 20) – 25х= 30 · 15;

24х+ 480 – 25х= 450;

– х= –30;

х= 30.

Значит, первоначально в растворе было 30 г соли.

Ответ: 30 г.

4. № 797.

Решение:

Преобразуем левую часть равенства:

(10a + b) (10a + c) = 100a² + 10ac + 10ab + bc = 100a² + 10a (b + c) + bc.

Преобразуем правую часть равенства:

100а(а+ 1) +bc= 100a²+ 100a+bc.

У полученных выражений есть одинаковые слагаемые. Это 100a²иbc. Но еслиb +c= 10, то 10а(b +c) = 10а· 10 = 100а, то есть все слагаемые у этих выражений равны. Значит, данное равенство верно при условии, чтоb +c= 10.

а) 23 · 27.

Здесь а= 2,bc= 3 · 7 = 21. Имеем:

23 · 27 = 100 · 2 · 3 + 21 = 621.

б) 42 · 48.

Здесь а= 4,bc= 2 · 8 = 16. Имеем:

42 · 48 = 100 · 4 · 5 + 16 = 2016.

III. Итоги урока.

– Что называется многочленом? Степенью многочлена?

– Как умножить одночлен на многочлен?

– Как умножить многочлен на многочлен?

– Какие вы знаете способы разложения многочлена на множители?

– Опишите алгоритм способа группировки разложения многочлена на множители.

Домашнее задание:№ 754 (г, е); № 762; № 778 (б, г); № 787.

Урок 81 Деление с остатком

Цели:изучить, как может быть представлено любое целое число при делении его с остатком на некоторое натуральное число; использовать данное представление при решении задач на делимость чисел.

Ход урока

I. Актуализация знаний.

Учащиеся уже умеют делить с остатком натуральные числа. Можно дать им выполнить несколько таких заданий и записать полученные результаты:

17 : 2 = 8 (ост. 1); 20 : 3 = 6 (ост. 2); 23 : 5 = 4 (ост. 3).

Затем предложить учащимся записать числа 17, 20 и 23, используя делитель, частное и остаток:

17 = 8 · 2 + 1; 20 = 6 · 3 + 2; 23 = 4 · 5 + 3.

II. Изучение нового материала.

1. Рассмотреть деление целых чисел на натуральные с остатком и снова прийти к равенствам, подобным тем, которые были получены на этапе актуализации. Например:

–13 = 5 · (–3) + 2; –20 = 7 · (–3) + 1; –32 = 3 · (–11) + 1.

2. Делается выводо том, что любое целое числоапри делении на натуральное числоb может быть записано в виде:

a=bq+r, гдеq– частное от деления,

r– остаток, 0 ≤r<b.

Данное утверждение доказывается.

3. Рассматривается вопрос о разбиении чисел на классы при делении с остатком.

III. Закрепление изученного материала.

1. № 724.

Решение:

Если число апри делении на 7 даёт в остатке 3, то оно может быть записано в виде:

а= 7q+ 3, гдеq– частное от деления.

Перебирая различные q, будем получать искомые числа:

q= 0,а= 7 · 0 + 3 = 3;

q= 1,а= 7 · 1 + 3 = 10;

q= 2,а= 7 · 2 + 3 = 17 (не удовлетворяет условию);

q= –1,а= 7 · (–1) + 3 = –4;

q= –2,а= 7 · (–2) + 3 = –11;

q= –3,а= 7 · (–3) + 3 = –18 (не удовлетворяет условию).

Ответ: –11, –4, 3, 10.

2. № 726.

Решение:

Если число тпри делении на 35 даёт в остатке 15, то оно может быть записано в виде:

т= 35q+ 15, гдеq– частное от деления.

Каждое слагаемое этой суммы делится на 5, значит, и вся сумма делится на 5.

Первое слагаемое суммы делится на 7, а второе не делится, значит, вся сумма не делится на 7.

Ответ: на 5 делится, на 7 не делится.

3. № 727.

Решение:

Согласно условию число аможет быть записано в виде:

a=bc+d.

Если числа b,cиdнечётные, то приходим к следующим выводам:

1) число bc– нечётное (как произведение двух нечётных чисел);

2) число bc+d– чётное (как сумма двух нечётных чисел).

Получится следующее: если числа b,cиdнечётные, то числоабудет только чётным. Значит, числаа,b,cиdне могут быть одновременно нечётными.

4. № 728.

Решение:

Если числа аиbпри делении на 3 дают различные остатки, то они могут быть записаны в виде:

а= 3q+ 1 иb= 3р+ 2.

Найдем число аb+ 1:

аb+ 1 = (3q+ 1) (3р+ 2) + 1 = 9рq+ 6q+ 3р+ 3.

Каждое слагаемое полученной суммы делится на 3, значит, и вся сумма делится на 3.

5. № 730.

Решение:

Если при делении числа ана 12 получается остаток 5, то числоаможет быть записано в виде:

а= 12q+ 5, гдеq– частное от деления.

При делении числа а= 12q+ 5 на 4 первое слагаемое суммы разделится на 4 без остатка, а второе даст в остатке 1. Значит, числоапри делении на 4 даст в остатке 1.

Ответ: 1.

6. № 732.

Решение:

Если число апри делении на 5 даёт в остатке 1, то оно может быть записано в виде:

а= 5q+ 1, гдеq– частное от деления.

Если же это число при делении на 7 даёт в остатке 1, то его можно записать так:

а= 7р+ 1, гдер– частное от деления.

По условию qбольшерна 4. Получим систему уравнений:

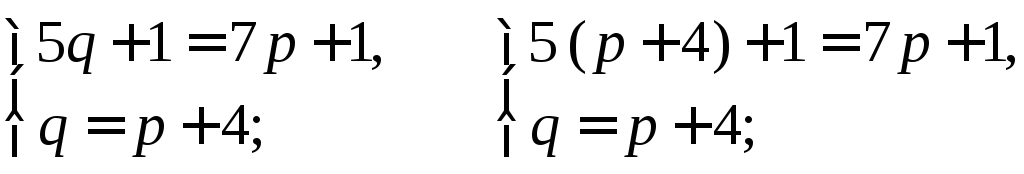
5р+ 20 + 1 = 7р+ 1;

2р= 20;

р= 10.

Найдем число а:

а= 7р+ 1 = 7 · 10 + 1 = 71.

Ответ: 71.