Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Украинская государственная академия железнодорожного транспорта

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

1545

.pdf

Скачиваний:

Добавлен:

10.04.2015

Размер:

452.97 Кб

Скачать

☆

<<< < Предыдущая 12 / 42 3 4 > Следующая >>>

f ( x, y ) = f ( x0 , y0 ) ± δ f .

ПОХІДНІ СКЛАДНИХ ФУНКЦІЙ

Нехай

z = f (u; v) ,

де

u = u(x),

v = v(x) ,

тобто

z = f (u( x); v( x)) = g( x)

– складна функція однієї змінни x . Тоді

(4)

∂z du

∂z dv

+ ¶v

¶u

Приклад. а)

z = (sin x)tgx

= uv , де u = sin x, v = tg x . Знайти

∂z

∂z = (u v )v' = uv ln u , за формулою (4) маємо

= (uv )u' = vu v−1;

¶u

¶v

v du

= vuv−1

+ uv ln u

= u v

+ ln u

u dx

tg x

ln(sin x)

= (sin x)

cos x + ln(sin x)

(sin x)

sin x

cos2 x

Нехай

z = f (u; v) ,

де

u = u(x; y), v = v(x; y) ,

тобто

z = f (u(x; y);v(x; y)) = g(x; y)

– складна функція двох змінних. Тоді її

частинні похідні

∂z

∂z ∂u

∂z ∂v

∂z

∂z ∂u

∂z ∂v

(5)

¶x =

+ ¶v ¶x

¶y =

¶y

¶v ¶y

¶u

¶x

¶u

Приклади. Знайти частинні похідні складених функцій.

а) z = sin xy cos

= sinu cosv , де u = xy, v =

∂z

Обчислимо

x .

За першою з формул (5) маємо

∂z

(sinu × cosv)

∂u

+ (sin u × cosv)

' ∂v

¶x

v ¶x

= cosu ×cos v × y - sin u ×cos v(- yx −2 ) = y × cos xy cos

sin xy sin

x 2

Обчисліть ∂z / ∂y

самостійно.

б) z = x3 + 2 y2 , де x = uv , y =

;

∂z

∂z ×

∂x

∂z

∂y

= 3x2 × v + 4 y ×

¶u

¶x

¶u

¶y

¶z =

¶z ×

¶x +

¶z

¶y = 3x2 × u + 4 y

, де x = uv , y =

¶v

¶x

¶v

¶y

¶v

в) z = ln(3y + 2x2 ) , де x = u2 , y =

;

dz ∂z dx ∂z dy

- u

, де x = u2 , y =

;

= ¶x ×

× 2u -

¶y

3y + 2x2

2x2 + 3y

(1 - u )2

1 - u

г)

z = arctg

, де x = u2 - v2 .

∂f

dz ∂x

∂z

dz ∂x

−v

¶u

¶v =

× ¶v =

, де x = u2 - v2 .

¶u

(1 + x)

Формули

(4), (5)

легко

розповсюджуються

на

випадки функцій більш ніж двох змінних. Наприклад, якщо z = f (u;v;w) , деu = u(x), v = v(x), w = w(x) , тоді

∂z

+ ∂z

∂z

¶u dx

¶w dx

¶v dx

ЧАСТИННІ ПОХІДНІ ВИЩИХ ПОРЯДКІВ

Розглянемо функцію

z = f ( x; y) . Її частинні похідні

zx '= f x '( x; y) й z y '= f y '( x; y) самі є функціями двох змінних.

Частинні похідні від частинних похідних називаються

частинними похідними другого порядку. Функція двох змінних має, таким чином, чотири частинні похідні другого порядку:

повторні похідні:

¶2 z = f xx'

= ( f x' )'x

¶2 z

= f yy'

= (f y' )'

¶x 2

¶y 2

¶2 z

¶z

¶2 z

¶ ¶z

мішані похідні:

= f

' = ( f ' )

= f

= (f

' ) .

¶x¶y ¶y ¶x

¶y¶x ¶x ¶y

Приклад.

z = x2 y + 4xy2 + x2 - y + 5

zx '= 2xy + 4 y2 + 2x, z y '= x2 + 8xy - 1; zxx' = 2 y + 2, z yy' = 8x,

zxy' = ( zx') y' = 2x + 8 y, z yx' = (z y' ) x' = 2x + 8 y .

Частинні похідні zxy' та z yx' виявилися рівні, що відбулося

зовсім не випадково.

ТЕОРЕМА. Якщо функція z = f ( x; y) ,

її перші похідні zx' ,

z'y

та змішані похідні zxy' та z yx' неперервні в деякій області, то мішані похідні zxy' та z yx' в цій області рівні .

Наслідок. Результат повторного диференціювання не

залежить	від	порядку диференціювання (наприклад
zxyy' = z yxy'	= z yyx' ),	якщо всі виникаючі при обчисленнях похідні

неперервні.

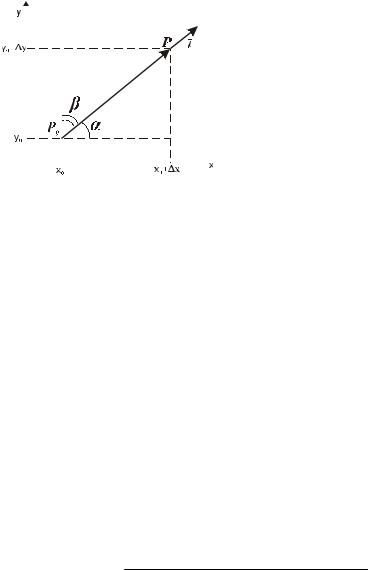
ПОХІДНА ЗА НАПРЯМКОМ

Рисунок 5.

Очевидно, що

Нехай z=f(P) – функція двох змінних, що диференціюється

				→	= (l x ; l y			)
в околі точки P ( x		; y	0	) , l	= (l x ; l y			)
0	0		0
– вектор, що задає деякий
напрямок, P( x0 +	x; y0 +				y) –
точка на цьому напрямку
		→
(така, що вектор P0P				→
				→
колінеарний вектору l
(рис. 5)).
x = ρ cos α, y = ρ cosβ, де ρ = ρ (P0 ; P) =							,	а
						P0 P
						P0 P

cos α =

, cos β =

l y

– напрямні

косинуси вектора, тобто

→

| l

| l |

→

косинуси кутів між вектором

і осями координат Ох і Oy

відповідно.

z = f (P) − f (P ) = f (x

+ x; y +

y) − f (x ; y )

Величина

0 0

називається приростом функції в даному напрямку.

Границя відношення цього приросту до величини

переміщення l = ρ при умові

→ 0 називається похідною за

напрямком

∂z = l i m	l z
∂l l →0	l

→

l та позначається ∂z / ∂l ,

= l i m f ( x0 + x; y0 + y) − f ( x0; y0 ) . l →0 l

Нескладно одержати більш зручні формули для обчислення похідної за напрямком, а саме, для функції двох змінних z = f(x;y)

∂z	=	∂f	cosα +	∂f	cos β	;	(6)
∂l	=	∂x	cosα +	∂y	cos β	;
∂l		∂x		∂y

для функції трьох змінних u

= f

( x; y; z)

(7)

∂u

∂f

∂l =

∂x cos α +

∂y cos

β + ∂z cos

= (l x ; l y ; lz )

→

де напрямні косинуси

тривимірного

вектора

відповідно рівні

c o s α =

l x

, c o s β

l y

, c o s γ =

l z .

(8)

→

| l

| l |

Похідна за напрямком характеризує швидкість зміни

→

функції в даному напрямку l .

→

Приклади. Знайти похідну за напрямком l та обчислити її значення в точці А.

→

а) z = arccos(x2 - 2 y) , l = i − 3 j , P0(4;8).

→

(1;−3).

Знайдемо

напрямні

косинуси

вектора

cosα =

, cos β =

-3

= -

→

+ (-3)2

| l |

Обчислимо частинні похідні z = arccos(x2 - 2 y) .

z¢x =

z¢y =

. За

- (x2 -

2 y)2

- (x2 - 2 y)2

похідна за напрямком

∂z =

¶l

1 - (x2 - 2 y)2

- (x2 - 2 y)2

2x - 6

- (x2 - 2 y)2

Обчислимо її значення у точці P0(4;8)

¶z (P ) =

2 × 4 - 6

¶l

1 - (42 - 2 ×8)2

→

б) u = xy − 2 y + xz3 , l = (− 3; 4;0), P0(1;2;0).

Обчислимо модуль вектора

формулою (6)

× (- 3 ) =

→	+ l y2 + lz2
\| l \|= lx2	+ l y2 + lz2	= (−3)2 + 42 + 02 = 5. За формулами (8) маємо

cosα = −3/ 5, cosβ = 4 / 5,cosγ = 0 / 5. Обчислимо частинні похідні

, u y '= x - 2 , u z '=

u x '= y + z 3 ×

z .

За формулою (7) маємо похідну за напрямком

¶u

- 3

4( x - 2)

( x - 2) ×

xz × 0 = -

y +

¶l

2 x

5 2

та її значення в точці P0(1;2;0)

∂u(P )

4(1 − 2)

= −

−

= −2 .

2 +

∂l

→

Оскільки ∂u / ∂l <0, то функція в напрямку l

спадає.

ГРАДІЄНТ

Градієнтом функції gradz (або Ñz ) кількох змінних називається вектор, координати якого є частинними похідними за відповідними незалежними змінними.

Таким чином, для функції двох змінних z = f (x; y)

¶z

¶z ;

¶z

grad z =

× i

× j =

¶x

¶y

¶x

¶y

а для функції

трьох змінних u = f ( x; y; z)

grad u =

¶u

× i +

¶u

× j

¶u

¶u ¶u ¶u

¶x

¶y

¶z

× k =

;

¶x

¶y

¶z

(9)

(10)

Говорять, що в області G Rn (n=2, 3) задано векторне поле, якщо в кожній точці P G заданий вектор F = F (P) (тобто задана вектор-функція декількох змінних). Отже, будьяка диференціюєма в області G скалярна функція (скалярне поле) u=u(P) породжує в цій області векторне поле F ( p) = grad u(P) . Функція u(P) називається потенціалом векторного поля F = grad u , а саме векторне поле F

називається потенційним полем.

ТЕОРЕМА. Похідна за напрямком дорівнює проекції

градієнта на цей напрямок	∂u = прUlR grad u .
	∂l
Наслідок. Похідна за напрямком максимальна у напрямку
градієнта, тобто градієнт	направлений		у	бік	найскорішого
зростання функції, і в цьому напрямку		∂u		∂u	= \|grad u \|.
зростання функції, і в цьому напрямку		∂l	=		= \|grad u \|.
		∂l		∂l max

ТЕОРЕМА. 1). Градієнт функції двох змінних z = f (x; y) в кожній точці P0 (x0 ; y0 ) перпендикулярний до лінії рівня даної функції, що проходить через цю точку (якщо grad u(P0 ) ¹ 0 ).

2).	Градієнт	функції трьох змінних u = f ( x; y; z) в кожній
точці	P0 ( x0 ; y0 ; z0 )	перпендикулярний до поверхні рівня даної

функції, що проходить через цю точку (якщо grad u(P0 ) ¹ 0 ).

	Наслідок. Похідна за напрямком l , який дотичний до лінії
рівня, дорівнює нулю.
	Приклади. Знайти градієнт функції в точці М.
а)	z = (13 + 2 y)x , M (3; −6) .
	Обчислимо частинні похідні
z¢x	= (13 + 2 y)x ln(13 + 2 y), z¢y = 2x(13 + 2 y)x−1.

За формулою (9) маємо

grad z = (13 + 2 y)x ln(13 + 2 y)i + 2x(13 + 2 y)x−1 j.

Обчислимо значення градієнта в точці М(3;-6)

grad z = (13 + 2 × (-6))3 ln(13 + 2 × (-6))i +

+2 ×3(13 + 2 × (-6))3−1 j = 0 + 6 j = 6 j.

б)u = ln(xy) + x arcsin z ,

M (2; −1;0) .

Обчислимо частинні похідні

∂u =

× y + arcsin z =

+ arcsin z ;

∂u =

∂u = x

¶x

× x =

;

. За формулою (10) маємо

¶y

¶z

- z

1 - z

× k .

grad u =

+ arcsin z

× i +

× j

1 - z

Обчислимо значення градієнта в точці											M (2;−1;0) :
1				1		2				- j + 2k .
grad u(M ) =	+ arcsin 0	× i +			× j +				× k = 0,5i
grad u(M ) =	+ arcsin 0	× i +	-1		× j +				× k = 0,5i
2			-1		1	-	0	2
					1	-	0
НЕЯВНІ ФУНКЦІЇ ТА ЇХ ДИФЕРЕНЦІЮВАННЯ
Розглянемо рівняння
		F ( x; y; z) = 0									(11)
Якщо для всіх (x;y)				з деякої множини							D R2 існує така

функція (не обов'язково єдина), при підстановці якої в (11) ця рівність виконується тотожно в D, то говорять, що рівняння

(11) визначає на множині D неявну функцію z = z( x; y) .

Приклад. Рівняння x2 + y2 - z2 = 0						визначає		неявно дві
неперервні	функції	z =			та z = −			(або одну
				x 2 + y 2			x 2 + y 2

двозначну	функцію	z = ±	x2 + y2 )		з	областями		визначення
кожної D = R 2 .
Проте	отримати	явну		залежність			z = z( x; y)	з рівняння

вигляду (11) не завжди можливо, до того ж воно може і не визначати ніякої функції. Тому важливо знать умови, які б гарантували існування такої неявно заданої функції z = z( x; y) .

ТЕОРЕМА. Про існування неявної функції.

Нехай

функція F ( x; y; z)

та

її

частинні

похідні

F '( x; y; z) ,

'( x; y; z) , неперервні в околі точки M

. Якщо

F ( x; y; z) = 0 та F

'( x

; y

; z

) ¹ 0 ,

то рівняння

F ( x; y; z) = 0

має єдиний неперервний розв’язок

z = ϕ(x; y)

у деякому околі

точки P ( x

; y

) R2

таке, ϕ (x ; y ) = z

Функція

ϕ(x; y)

також

має

неперервні частинні похідні.

Зауважимо,

що якщо в точці M

похідна F '(x ; y ; z

) = 0 , а,

0 0

наприклад,

F '(x ; y ; z

) ¹ 0 , то рівняння

F ( x; y; z) = 0

може

не

y 0

0 0

визначати z як функцію x та y , але визначає y як функцію x та z .

Помітимо, що теорема не вказує метод знаходження цієї неявної функції, а тільки стверджує, що така функція існує. Проте виявляється, що частинні похідні zx ' і z y ' цієї невідомої

функції можуть бути обчислені.

Нехай умови теореми про існування неявної функції

виконані,	і	рівняння F ( x; y; z) = 0			визначає деяку		функцію
z = z( x; y) .	Підставляючи		її в	рівняння		(11), отримаємо
тотожність,			F (x; y; z(x; y)) = 0
			F (x; y; z(x; y)) = 0
справедливу		при всіх	(x; у)	з	деякого	околу	точки P0 .

Продиференціюємо обидва частини цієї тотожності по змінні x, використовуючи правило диференціювання складної функції.

' × x

'+F

' × y

'+F ' × z

'≡ 0 F

' + F ' × z

'≡ 0

- F '

(12)

F '

Аналогійно визначається і частинна похідна z y ':

' × y

'+F

' × y

'+F ' × z

'≡ 0 F

+ F ' × z

'≡ 0

- Fy'

(13)

F '

Ці формули виражають частинні похідні неявної функції

z = z( x; y)

через

похідні

заданої функції

F (x; y; z) .

При

'(x ; y ; z

) = 0

ці формули втрачають сенс.

Зауваження.

разі,

коли

рівняння F (x; z) = 0 неявно

визначає функцію однієї змінної, що диференціюється,

можна,		діючи аналогійно,					обчислити звичайну похідну
z '( x) =	- F		'
z '( x) =		x , якщо F ' ¹ 0 .
	F	'	z
	F	'
	z
Приклад. Знайдемо частинні похідні функції z , заданої
рівнянням F (x; y; z) º x2 + y2 + z2 -1 = 0 . Маємо
			∂F = 2x,		∂F = 2 y,					∂F = 2z;
			¶x		¶y					¶z
отже			∂z = -					∂z
				x		,		∂z	= -	y	.
						,			= -		.
			¶x z					¶y		z

В цьому прикладі можна знайти явний вираз функції і перевірити правильність отриманих результатів. Пропонуємо зробити це самостійно.

ДОТИЧНА ПЛОЩИНА ТА НОРМАЛЬ ДО ПОВЕРХНІ

ДО ПОВЕРХНІ. ГЕОМЕТРИЧНИЙ ЗМІСТ

ДИФЕРЕНЦІАЛА

Геометричний зміст диференціала функції двох змінних


	z = f ( x; y)	пов'язано		з	дотичною
	площиною	до	поверхні,			яка
	визначаєтьсяною цією функцією.
	Нехай	z = f ( x; y)		функція, що
	диференціюється		в	околі		точки
	P0 ( x0; y0 ) , а поверхня S – її графік.
Рисунок 6	Розглянемо	перетин			поверхні
Рисунок 6	площиною y = y0 і проведемо дотичну
	площиною y = y0 і проведемо дотичну
пряму в точки P0 до лінії перетину.			Аналогійним			чином

побудуємо дотичну до лінії перетину площиною x = x0 (рис.6). Площина, що проходить через ці дві дотичні, які перетинаються, називається дотичною площиною до

поверхні z = f ( x; y) в точці P0 ( x0; y0 ) . Її рівняння

z - z0 = f x'( x0; y0 ) × (x - x0 ) + f y'( x0; y0 ) × ( y - y0 )

(14)

де z0 = f ( x0; y0 ) .

Можна показати, що для будь-якої лінії на поверхні, що проходить через точку M 0 ( x0; y0; z0 ) , дотична пряма, проведена до лінії через цю точку, лежить в дотичній площині.

Вектор N , який перпендикулярен дотичній площини, називається нормальним вектором до поверхні.

Пряма, перпендикулярна до дотичної площини, що проходить через точку дотику, називається нормаллю до поверхні в даній точці.

З рівняння (14) вектор N = { f x'(x0; y0 ) : f y'(x0; y0 ); - 1} є нормальним до поверхні z = f ( x; y) (причому будь-який вектор,

пропорційний йому, N λ = l ×{ f x'; f y'; - 1} – теж нормальний).

Звідси випливає, що рівняння нормалі до поверхні в точці M 0 ( x0; y0; z0 ) має вигляд

x − x0

y − y0

z − z0

(15)

f x'( x0; y0 )

f y'(x0; y0 )

- 1

Нехай

тепер

поверхня

S задана неявним рівнянням

F (x; y; z) = 0 ,

яке

визначає

околі точки P0 ( x0; y0 )

диференційовану

функцію

z = f ( x; y) ,

причому

z0 = f ( x0; y0 ) .

Згідно правил

диференціювання

неявної функції

(12)-(13)

(якщо F

'( x

; y

; z

) ¹ 0 )

- F

- Fy'

→

- F

- Fy'

N =

f x '=

' , f y '=

' ;

; -1 .

F '

Для

зручності

помножимо

на

множник

l = -F ',

→

отримаємо інший нормальний вектор N = {Fx'; Fy'; Fz'} , де всі похідні обчислюються в точці M 0 ( x0; y0; z0 ) . Таким чином, приходимо в цьому випадку до рівняння нормалі

x − x

y − y

z − z

(16)

Fx'(M 0 ) Fy'(M 0 ) Fz'(M 0 )

Відмітимо, що рівняння дотичної площини можна

записати у вигляді

Fx'(M 0 )( x - x0 ) + Fy'(M 0 )( y - y0 ) + Fz'(M 0 )( z - z0 ) = 0

(17)

Хоча

раніше

було

зроблено

припущення,

що

'( x

; y

; z

) ¹ 0 ,

але

рівняння

(16),(17)

справедливі і

коли

'( x

; y

; z

) = 0 .

Вони не мають сенсу тільки в тому випадку,

якщо все три частинні похідні дорівнюють нулю одночасно.

Точка M 0 ( x0; y0; z0 ) називається особливою точкою

поверхні F ( x; y; z) = 0 , якщо F '(M

) = 0,

F '(M

) = 0,

F '(M

) = 0 .

В особливій точці дотична площина і нормаль до поверхні не визначені.

Приклади. Скласти рівняння нормальної прямої та дотичної площини

<<< < Предыдущая 12 / 42 3 4 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
12.11.2019530.94 Кб81. Плани семінарських занять з історії України.doc
#
10.04.2015116.22 Кб1910 Бронювання.doc
#
15.03.20161.19 Mб191003.doc
#
16.07.2019889.34 Кб4102.doc
#
15.03.2016476.16 Кб1810_Dzyuba_Pechiy_UkrDAZT.doc
#
10.04.2015452.97 Кб101545.pdf
#
10.04.201515.39 Кб231_1_Sotsiologiya_sim (1).docx
#
10.04.20151.07 Mб422 Електронна версія конспекту лекцій.doc
#
10.04.2015238.7 Кб62 Технологічний процес виготовлення колектора.docx
#
10.04.2015842 Кб272009 170Л Маркетинг услуг Парасюк з.pdf
#
10.04.20155.79 Mб622012_11_Metod_vkaz_ch_1_Str_mat.doc