
lekcii_dm
.pdf
В этом случае о функции f (x1, x2,…, xn) будем говорить, что данный функциональный элемент ее реализует, и такой элемент будем изображать так, как показано на рис.5.2.
1 2 |
n |

 …..
…..
f
Рис. 5.2. Реализация функционального элемента булевой функции f (x1, x2,…, xn).
Из функциональных элементов определяется схема из функциональных элементов (точнее схема из функциональных элементов в соответствующем
логическом базисе), как-то: |
|
|||
1) |
, , ; |
3) |
, ; |
5) х у; |
2) |
, ; |
4) |
1, , ; |
6) х ↓ у |
и т.д.
Замечания.
1. Учитывая, что существуют определённые аналитические преобразования одного логического базиса в другой, можно изображать схемы в любом логическом базисе и преобразовывать их в другие. Базис, состоящий из логических функций , , называется нормальным; из логических функций , или , – неполным нормальным; из стрелки Пирса х ↓ у – базисом Вебба; из штриха Шеффера х у – базисом Шеффера.
Как известно, базис Вебба и базис Шеффера связаны с нормальным базисом следующими аналитическими соотношениями:
х у = х у; и обратно, х = х х; х у = (х х) (у у);
171

х ↓ у = х у; и обратно, х = х ↓ х; х у =(х ↓ х) ↓ (у ↓ у).
Переход от схемы в нормальном базисе к базисам Шеффера и Вебба
и обратно, например, можно отобразить в следующей таблице (таблица 5.1).
Таблица 5.1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Нормальный базис |
|
|
|
Базис Шеффера |
|
|
|
|
Базис Вебба |
|
||||||||||||||||||||||||||||||
|
|
|
не |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
y = x1 |
x |
|
|
|
|
|
|
|
|
|
y = x1 |
|
|||||||||
x |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
y = x x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
x |
|
|
|
y = x x |
|
x1 |
|
1 |
|
2 |
|
y = x1x2 |
|
|
|
|
|
|
|
|
|
|
|
y = x x |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
x2 |
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
или |
x |
1 |
|
|
|
|
|
|
|
x1 |
x1 x2 |
|
y = x x |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
x |
|
|
y = x x |
2 |
|
|
|
|
y = x1 x2 |
|
|
|
|
|
|
1 |
2 |
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
1 |
|
|
1 |
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
x2 |
|
|
|
x2 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.Логические функции, кроме их реализации функциональными схемами, реализуются также контактными, релейно-контактными и интегральными схемами.
3.Одна и та же схема (функциональная, контактная, релейноконтактная, интегральная) может быть реализована большим или меньшим числом функциональных базисных элементов (функций), для уменьшения
172
которых, реализующих одну и ту же булеву функцию, разработана теория минимизации нормальных форм.
5.02. Основные понятия булевых функций.
Теорема.
Число всех различных булевых функций от n аргументов равно 22n .
Доказательство:
Число различных наборов переменных x1, x2, … , xn, где xi {0,1} равно k=2n. Так как каждая булева функция принимает только 2 значения: 0 или 1,
то число всех булевых функций от n переменных равно 2k 22k , что и требовалось доказать.
Определение.
Операцией сложения по модулю два, которая обозначается знаком , на множестве из двух элементов 0 и 1 называется операция со следующим законом композиции:
для a имеет место
a a 0 ; a 0 0 a a .
Определение.
Элементарными булевыми функциями называются следующие функции:
e1(x) 0 – нуль-функция; e2(x) 1 – единица-функция; e3(x) x – функция x;
173
e4(x) = x – отрицание x;
x y x & y x y xy – конъюнкция x и y; x y – дизъюнкция x и y;
x y – импликация x и y; x y – эквиваленция x и y;
x y – сложение по модулю два x и y.
Замечания.
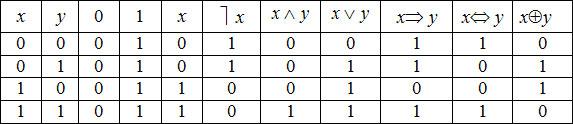
1. Таблица истинности для элементарных булевых функций имеет вид, представленный в табл. ниже.
Таблица
2. Заметим, что |
|
|
1) x y = ( x y), то есть |
e9(x, y) = e4(e8(x, y)), то есть функция x y |
|
является суперпозицией функций x y и x. |
|
|
2) x y z – суперпозиция функций x y и |
x y , каждая из которых |
|
от двух переменных. |
|
|
3) 0 = (x x); 1=x x. |
|
|
Приоритеты логических операций.
Операция имеет больший приоритет, чем ; Операция имеет больший приоритет, чем ; Операция имеет больший приоритет, чем ; Операция имеет больший приоритет, чем ;
174

Операция имеет больший приоритет, чем .
Примеры функций, являющихся суперпозициями элементарных функций. g1(x1, x2, x3, x4) x1x2 x3 x4
g2(x1, x2, x3) (x1 x2)(x2 x3 x1 x2) g3(x1, x2) (x1 x2) x1x2 x2
Определение.
Пусть
1) u – переменная, при этом пусть u0= u, а u1=u;
2)ai {0,1} , i 1,n ;
3)u1, u2, … , un – переменные, причём не обязательно различные.
Тогда |
формула |
ua1 |
ua2 |
... uan |
называется |
элементарной |
||
1 |
2 |
n |
||||||
конъюнкцией, а |
ua1 |
ua2 |
... uan |
– элементарной дизъюнкцией. |
||||
1 |
2 |
|
n |
|||||
Примеры. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. |
Элементарными конъюнкциями будут следующие формулы: |
||||||||||||||||||||
|
x y, x1 x1, x |
|
|
|
, |
|
x1, |
|
|
|
x2, |
|
|
x2 x3 x4 . |
|||||||
x, y, x, |
y |
x |
x1 |
x1 |
x1 |
x1 |
|||||||||||||||
2. |
Элементарными дизъюнкциями будут следующие формулы: |
||||||||||||||||||||
|
|
|
|
|
|
x, x1 x1 |
|
, x1 |
|
|
|
x3, |
|||||||||
x, |
y, |
y, |
x y, |
x |
x |
x1 |
x1 |
x1 |
|||||||||||||
x1 x1 x2 y ,x1 x2 x3 x4 .
Ясно, что каждая элементарная конъюнкция и каждая элементарная дизъюнкция являются суперпозициями функций x, x y и x y.
175

Замечание.
|
|
|
|
|
|
|
u0 |
|
и u1 u , замечаем, что |
|
Принимая для переменной |
u , что |
u |
||||||||
ua = 1 u = a, a {0,1}. |
|
|
|
|
|
|
|
|||
В этом случае : |
|
|
|
|
|
|
|
|||
1) функция |
|
|
|
|
|
|
|
|||
|
|
|
xa1xa2...xan |
|
(1) |
|||||
Kn(x1, x2,…, xn) = |
1 2 |
n |
|
|||||||
такая, что Kn(a1, a2,…, an) = 1 |
и Kn(b1, b2,…, bn) = 0, если |
|||||||||
(b1, b2,…, bn) (a1, a2,…, an); |
|
|
|
|
||||||
2) функция |
|
|
|
|
|
|
|
|||
|
|
xa1 |
xa2 |
... xan |
|
|
(2) |
|||
dn(x1, x2,…, xn)= 1 |
2 |
|
n |
|
|
|||||
такая, что dn( |
|
, |
|
,..., |
|
) = 0 |
|
|||
a1 |
a2 |
an |
и dn(b1, b2,…, bn) = 1, если |
|||||||
(b1, b2,…, bn) (a1,a2,...,an ).
При этом в формулах (1) и (2) все переменные попарно различны.
Теорема.
Каждая булева функция является суперпозицией следующих функций: отрицания, конъюнкции и дизъюнкции.
Доказательство:
Первое доказательство.
Обозначим множество всех булевых функций через P2. Если данная функция f P2 является константой, равной нулю, то, согласно соотношению 0 = (x x) или 0 = x x, утверждение справедливо. В противном случае, существуют такие наборы (a1, a2,…, an), что f(a1, a2,…, an)=1. Для каждого такого набора (a1, a2,…, an) образуем элементарную конъюнкцию x1a1x2a2 ... xnan , которая имеет значение 1 только на наборе (a1, a2,…, an). Тогда
176
f(x1, x2,…, xn) = |
|
|
xa1 xa2 xan , |
(3) |
|
|
a1 |
,a2, ,an |
1 2 |
n |
|
|
f a1,a2, ,an 1 |
|
|
|
|
где дизъюнкции |
берётся |
по |
всем таким наборам (a1, |
a2,…, an), что |
|
f(a1, a2,…, an) = 1. Так как правая часть равенства (3) является суперпозицией требуемых функций, то теорема доказана.
Второе доказательство.
Если функция f P2 является константой равной 1, то, согласно 1= x x или 1= (x x), утверждение справедливо. В противном случае, существуют такие наборы (a1, a2,…, an), что f(a1, a2,…, an) 1, или, что то же самое, f(a1, a2,…, an) = 0. Таким образом, функция f(x1, x2,…, xn) может быть представлена в виде
|
|
(x |
a1 |
x |
a2 |
... x |
an |
) |
|
(a1,a2 |
,...,an ), |
1 |
2 |
n |
|
||||
|
|
|
|
, |
(4) |
||||
f(x1, x2,…, xn) = f (a1,a2,...,an ) 0 |
|
|
|
|
|||||
где конъюнкция берётся по всем таким наборам (a1, a2,…, an), что f(a1, a2,…, an)=0. Правая часть равенства (4) опять, как и в первом
доказательстве, является суперпозицией требуемых функций. Теорема доказана.
Определение.
Правая часть равенства (3) называется совершенной дизъюнктивной нормальной формой (кратко СДНФ) функции f(x1, x2,…, xn).
Замечание.
СДНФ существует только для тех булевых функций, которые не являются константами, равными нулю.
Определение.
177

Правая часть равенства (4) называется совершенной конъюнктивной нормальной формой (СКНФ) функции f(x1, x2,…, xn).
Замечание.
СКНФ существует только для тех булевых функций, которые не являются константами, равными единице.
Определение.
Конъюнкция всех аргументов функции (с отрицанием и без отрицания) называется полной и обозначается буквой K с соответствующим индексом. Индексом в обозначении служит номер набора или двоичное число, а также соответствующее ему десятичное, полученное при замене каждой переменной xi символом 1, а переменной xi – символом 0.
Определение.
Дизъюнкция всех аргументов функции (с отрицанием и без отрицания) называется полной и обозначается (в литературе) буквой D с соответствующим индексом. Индексом служит инверсионный номер набора или двоичное число, а также соответствующее ему десятичное, полученное при замене каждой переменной xi символом 0, а переменной xi – символом
1.
Примеры.
1. x1x2 – номер набора –112 = 310, полная конъюнкция обозначается K3.
2. x1x2 x3 – номер набора – 0102 = 210, полная конъюнкция обозначается K2.
178

3.x1 x2 – номер инверсионного набора – 002 – 010, полная дизъюнкция обозначается D0.
4.x1 x2 x3 – номер инверсионного набора – 1012 – 510, полная дизъюнкция обозначается D5.
Определение.
Полная конъюнкция, принимающая значение 1 только на одном наборе аргументов, соответствующем её индексу, и значение 0 на всех остальных наборах, называется также конституэнтой (образующей) или характеристической функцией единицы.
Определение.
Полная дизъюнкция, принимающая значение 0 только на одном наборе аргументов, соответствующем её индексу, и значение 1 на всех остальных наборах, называется также конституэнтой (образующей) или характеристической функцией нуля.
Замечание.
Значение булевой функции для конкретных значений аргументов удобно обозначить символом с индексом в виде десятичного числа, соответствующего двоичному набору аргумента, например, f(1,1) = 3, f(1,0,1) = 5.
Примеры.
С учётом введённых определений булеву функцию f(x1, x2) можно записать {с учетом разложения в СДНФ или СКНФ} в следующем виде:
3
f (x1,x2) x1x2 f (1,1) x1x2 f (1,0) x1x2 f (0,1) x1 x2 f (0,0) i 0 Ki i ;
179

f (x1,x2) (x1 x2 f (0,0))(x1 x2 f (0,1)) (x1 x2 f (1,0))
3
(x1 x2 f (1,1)) i&(0 Di i ).
Замечание.
Приведенный пример показывает, каким образом можно перейти от табличного представления булевой функции к её аналитическому представлению. При табличном представлении функции задаются её значения i для каждого набора аргументов, определяемого индексом i. Так как в силу определения операции конъюнкции имеем 0 Ki = 0 и 1 Ki = Ki, то для представления функции в виде СДНФ нужно выписать дизъюнкцию всех тех конституэнт единицы Ki, для которых i = 1. Учитывая также, что 0 Di=Di и 1 Di=1, СКНФ получается как конъюнкция всех тех конституэнт нуля Di, для которых значение функции i равно 0.
5.03. Законы двойственности.
Определение.
Учитывая определённую симметрию операций и в аксиоматике алгебры Буля логических высказываний и операций, операции и называются двойственными.
Определение.
Формулы 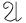 и
и 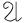 * называются двойственными, если одна получается из другой заменой каждой операции на двойственную.
* называются двойственными, если одна получается из другой заменой каждой операции на двойственную.
Примеры.
180
