
lekcii_dm
.pdf
4.02. Способы задания автоматов. Таблица переходов.
Определение.
Таблица переходов (таблица выходов) автомата Мили представляет собой таблицу, в которой левый столбец обозначается входными сигналами (алфавитом не терминалов), а верхняя строка – состояниями, начиная с начального состояния. На пересечении строки и столбца указывается следующее состояние, в которое переходит автомат (в таблице переходов) или выходной сигнал, выдаваемый им (в таблице выходов).
Представим автоматы Мили и Мура табличным способом.
Описание работы автомата Мили таблицами переходов и выходов иллюстрируется на примере автомата А1 (рис. 4.1): Х – алфавит входных сигналов; Y – алфавит выходных сигналов; Q - алфавит состояний; – функция переходов; X – функция выходов
а) |
б) |
Рис. 4.1. Таблицы переходов (а) и выходов (б) автомата А1.
Автомат, имея один вход и один выход, работает в дискретном времени, принимающем значения t = 1, 2, 3, ... На вход автомата поступают входные сигналы xf (например, сигналы x1 и x2). В каждый момент t автомат находится в некотором состоянии q(t), начиная с начального состояния q1.
На пересечении столбца qm и строки xf в таблице переходов ставится состояние qs = δ (qm, xf), в которое автомат переходит из состояния qm под действием сигнала xf, а в таблице выходов – соответствующий этому переходу выходной сигнал yg = λ (qm, xf).
121

Определение.
Иногда при задании автоматов Мили используют одну совмещенную таблицу переходов и выходов, в которой на пересечении столбца qm и строки xf записываются в виде qs / yg следующее состояние и выдаваемый выходной сигнал.
На рис. 4.2 представлена совмещенная таблица автомата А1.
Рис. 4.2. Совмещенная таблица автомата А1.
Определение.
Так как в автомате Мура выходной сигнал зависит только от внутреннего состояния и не зависит от входного сигнала, то он задается одной отмеченной таблицей переходов, в которой каждому ее столбцу приписан, кроме состояния qm еще и выходной сигнал yg = λ (qm), соответствующий этому состоянию.
Пример табличного описания автомата Мура А2 (рис. 4.3). Для частичных автоматов, у которых функции δ или λ определены не для всех пар (qm, xf) Q x X, на месте неопределенных состояний и выходных сигналов ставится прочерк или знак Ø.
122
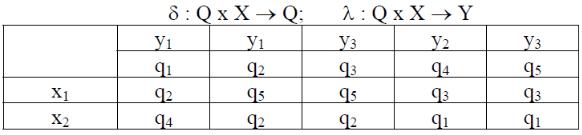
Рис. 4.3. Таблица переходов автомата Мура.
4.03. Способы задания автоматов. Граф автомата.
Часто автомат задают с помощью графа автомата.
Определение.
Граф автомата – ориентированный граф, вершины которого соответствуют состояниям, а дуги – переходам между ними. Две вершины графа автомата qm и qs (исходное состояние и состояние перехода) соединяются дугой, направленной от qm к qs, если в автомате имеется переход из qm в qs, то есть если qs = δ (qm, xf) при некотором xf Х. Данной дуге (qm , qs) приписывается входной сигнал xf и выходной сигнал yg = λ (qm , xf). При этом выходной сигнал yg записывается внутри вершины qm или рядом с ней.
На рис. 4.4 и 4.5 приведены графы автоматов А1 и А2, описанных ранее табличным способом.
123
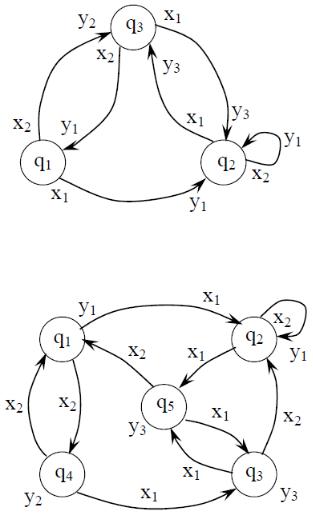
Рис. 4.4. Граф автомата А1
Рис. 4.5. Граф автомата А2
Любой автомат может быть задан с помощью графа, но не всякий граф в алфавитах Q, X, Y задает автомат. В графе автомата не должно существовать двух дуг с одинаковыми входными сигналами, выходящих из одной и той же вершины (условие однозначности).
4.04. Способы задания автоматов. Матрица переходов и выходов.
Определение.
124
Матрица переходов и выходов представляет собой таблицу с двумя входами. Строки и столбцы таблицы отмечены состояниями. Если существует переход из состояния qm под действием входного сигнала xf в состояние qs, с выдачей выходного сигнала yi, то на пересечении строки qm и столбца qs записывается пара xf / yi.
Для автомата Мура используется матрица, столбцы которой отмечены выходными сигналами yi, а на пересечении ее строк и столбцов указываются только входные сигналы xf.
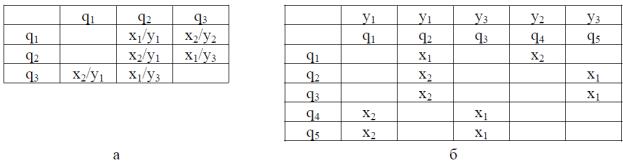
Ниже приведены матрицы переходов и выходов для рассмотренных ранее автоматов A1 и A2 (рис. 4.6).
Рис. 4.6. Матрицы переходов и выходов автоматов А1 (а) и А2 (б).
4.05. Машины Тьюринга и конечные автоматы.
Определение.
Машины Тьюринга представляют собой абстрактные устройства самого общего типа и являются обобщением автоматов Мили и Мура.
Машины Тьюринга наиболее близки к реальным ЭВМ, так как они представляют собой хорошую математическую модель вычислительной машины. Как показали многочисленные теоретические исследования, классам языков, соответствующим четырем типам грамматики по
125
классификации Хомского, можно поставить во взаимно-однозначное соответствие четыре типа распознающих устройств. Простейшим из них является класс так называемых конечных автоматов, которые допускают (распознают) все языки, порождаемые автоматными (регулярными) грамматиками, и только их.
Определение.
Детерминированным конечным автоматом называют следующую пятерку:
А = (X, Q, δ, q0, F),
где X = {x1, ..., xm} – входной алфавит (конечное множество входных сигналов);
Q = {q0, q1, ..., qn-1} – алфавит состояний автомата (конечное множество символов);
δ – функция переходов;
q0 Q – начальное состояние автомата;
F Q – множество состояний, называемых заключительными.
На содержательном уровне функционирование конечного автомата можно представить следующим образом. Имеется бесконечная лента с ячейками, в каждой из которых может находиться один символ из Х. На ленте находится цепочка символов α Х*. Ячейки слева и справа от цепочки не заполнены. Имеется некоторое конечное управляющее устройство с читающей головкой, которое может последовательно считывать символы с ленты, передвигаясь слева направо. При этом устройство может находиться в
126
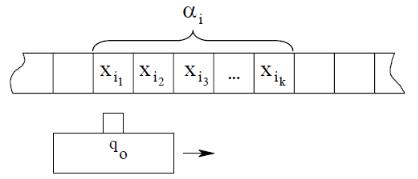
каком-либо одном состоянии из Q. Каждый раз, переходя к новой ячейке, устройство переходит к новому состоянию в соответствии с функцией δ.
На рис. 4.7 изображен конечный автомат в начальном состоянии q0, считывающий первый символ хi1 , входной цепочки αi . Стрелкой показано направление движения читающей головки. Отображение δ можно представить в виде совокупности так называемых команд, которые обозначаются следующим образом:
(q, x) → q′,
где q, q′ Q; x = X.
Рис. 4.7. Интерпретация конечного автомата.
Определение.
Число команд автомата конечно, левая часть команды (q, x) называется ситуацией автомата, а правая q′ – есть состояние, в котором автомат будет находиться на следующем шаге своей работы.
Графически команду удобно представлять в виде дуги графа, идущей из вершины q в вершину q′ и помеченную символом х входного алфавита
(рис. 4.8).
127

Рис. 4.8. Графическое представление команды автомата.
Определение.
Полностью отображение δ изображают с помощью диаграммы состояний, то есть ориентированного графа, вершинам которого поставлены в соответствие символы Q, а дугам – команды отображения δ.
Если автомат оказывается в ситуации (qj, xi), не являющейся левой частью какой-либо его команды, то он останавливается.
Определение.
Если управляющее устройство считает все символы цепочки α, записанной на ленту, и при этом перейдет в состояние qf F (заключительное состояние), то говорят, что цепочка α допускается автоматом А (автомат допускает цепочку α).
Определение.
Множество цепочек, допускаемых данным автоматом, называют языком этого автомата.
Отображение δ можно представить и в виде функции: δ (q, x) = q′,
где q, q′ Q; x X.
Эта функция интерпретируется так же, как и команда (q, x) → q′. Её можно распространить с одного входного символа на цепочку следующим образом: δ(q, ε) = q, где ε – пустая цепочка;
128
δ(q, αx) = δ(δ(q, α), x), где х Х, α Х*.
Таким образом, можно сказать, что α допускается автоматом А, если δ(q0, α) = qf , где qf F, а язык, допускаемый автоматом А, это
L(A) = {α | δ(q0, α) F}.
Пример.
Рассмотрим пример детерминированного конечного автомата А = (X, Q, δ, q0, F),
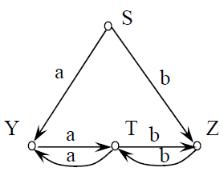
где Х = {a, b}; Q = {S, Y, Z, T}; q0 = S; F = {T}, а δ задается диаграммой состояний, представленной на рис. 4.9.
Рис. 4.9. Диаграмма состояний детерминированного конечного автомата
Очевидно, что язык, допускаемый этим автоматом, L(A) = {Mn | n ≥ 1},
где M = {aa, bb}.
Цепочка α1 = aabbaa, допускается данным автоматом, так как после ее просмотра автомат окажется в состоянии Т F.
Цепочка aabba не допускается, так как после ее просмотра автомат окажется в состоянии Y, не являющемся заключительным.
Цепочка abb не допускается потому, что после считывания символа а автомат окажется в ситуации (Y, b), для которой нет команды.
Определение.
129
Недетерминированный конечный автомат – есть пятерка того же вида. Единственное отличие заключается в том, что значениями функции переходов являются не состояния, а множество состояний (или, в терминах команд, возможны различные команды с одинаковыми левыми частями). Это соответствует тому факту, что в диаграмме состояний из одной вершины может исходить несколько дуг с одинаковой меткой.
4.06.Машины Тьюринга с двумя выходами.
Сточки зрения лингвистики машины Тьюринга можно рассматривать как распознающие устройства, допускающие языки самого широкого из рассмотренных классов: языки типа 0 или рекурсивно-перечислимые множества.
Определение.
Машина Тьюринга состоит из конечного управляющего устройства, входной ленты и головки, которая в отличие от головки конечного автомата может не только считывать символы с ленты, но и записывать на нее новые символы.
Лента считается бесконечной. Перед началом работы n ячеек ленты содержат символы входной цепочки αi = xi1 , xi2 ,..., xin, все остальные ячейки считаются заполненными специальным символом В («пустое место»), который не является входным (рис. 4.10).
130
