МКЭ_Лабораторная работа #1

Лабораторная работа № 1

Решение одномерной задачи методом конечных элементов

Цель работы: практическое знакомство с основными этапами применения метода конечных элементов (МКЭ) для приближенного решения краевой задачи (одномерный случай).

Задание

1.Ознакомиться:

a.с основными понятиями, назначением МКЭ;

b.с основными этапами МКЭ;

c.с прямым способом построения глобальной матрицы жесткости;

d.с предназначением и сутью метода Бубнова-Галеркина (Б-Г).

2.Решить методом конечных элементов указанную в индивидуальном задании краевую задачу, используя для построения уравнений МКЭ метод Б-Г. Этапы решения задачи:

a.разбиение области на конечные симплекс-элементы (количество элементов указано в индивидуальном варианте);

b.запись интерполирующих функций, определяющих элемент, в векторно-матричной форме, а также функций формы элемента;

c.формирование уравнения метода Б-Г для элемента, его вычисление, формирование локальных матриц жесткости и матриц нагрузок элементов;

d.включение локальных матриц элементов в глобальную матрицу жесткости и матрицу нагрузок;

e.учет граничных условий путем изменения глобальных матриц;

f.вычисление узловых значений искомой функции путем решения линейного матричного уравнения;

g.вычисление (если необходимо) приближенных значений искомой функции в заданных точках.

3.Оформить отчет, включив в него описание всех этапов решения задачи и полученные результаты.

Краткие теоретические сведения о решении задачи методом конечных элементов с использованием метода Бубнова-Галеркина

Краткое описание метода Бубнова-Галеркина

Одним из подходов к формированию уравнений для элементов является минимизация либо энергии деформации (в задачах механики деформируемого тела), либо функционала, связанного с рассматриваемым дифференциальным уравнением. Формирование такого функционала требует рассмотрения постановки задачи с позиций вариационного исчисления. Существуют другие, более простые способы получения уравнений для элементов. Один из способов, известный как метод Галеркина (Бубнова-Галеркина), был разработан для приближенного решения краевых задач. Метод Б-Г является одной из модификаций метода взвешенных невязок. Еще одной известной модификацией является метод наименьших квадратов, также применяемый в МКЭ.

Суть метода Б-Г состоит в следующем.

Пусть задано дифференциальное уравнение общего вида

(1)Lu f 0 ,

где L – дифференциальный оператор, u – неизвестная (искомая) функция, которую нужно аппроксимировать приближенной функцией, задаваемой в виде

u NiUi ,

i

1

решения ДУ (1), или невязка, выражается в виде

Lu f .

Величину мы стремимся минимизировать (т.е. хотим найти наиболее точное решение ДУ). Минимум невязки достигается при выполнении условия: функция невязки должна быть ортогональна аппроксимирующим базисным функциям. Это условие записывается для каждой базисной функции Ni в виде равенства

Ni dR 0 .

R

В МКЭ это равенство записывается для каждого элемента в виде уравнений

где L( ) – исходное ДУ, определяющее функцию (левая часть (1)), – искомая аппроксимирующая функция, которая выражается через базисные функции (они же функции формы в МКЭ) N и весовые коэффициенты (они же узловые значения искомой функции) следующим образом:

Вычисление интеграла (2) приводит к формированию системы линейных уравнений относительно узловых значений . Высший порядок производных, которые могут содержаться в L( ), не ограничен, он определяется физическим смыслом решаемой задачи. Однако высший порядок производных, допустимый в (2), на единицу больше порядка непрерывности интерполяционных соотношений. Если используются интерполяционные соотношения нулевого порядка непрерывности (непрерывна функция , но не ее первая производная), то в уравнения (2) могут быть включены производные не выше первого порядка. Преодоление этого ограничения возможно, если применить интегрирование по частям.

Замечание. Если граничные условия (первые производные искомой функции в граничных точках) не заданы, то соответствующие слагаемые, содержащие первые производные функции, в выражении, полученном в результате интегрирования (2), принимаются равными нулю (см. пример).

Прямое построение глобальной матрицы жесткости

Система линейных уравнений относительно узловых значений искомой функции формируется в матричном виде

K F ,

где [K] – матрица коэффициентов, называемая матрицей жесткости, [F] – вектор коэффициентов, называемый матрицей (вектором) нагрузок, а [ ] – вектор неизвестных – узловых значений функции.

Формирование матрицы жесткости1, выполняется вначале для каждого конечного элемента (локальные матрицы), после чего осуществляется процедура включения конечных элементов, в ходе которой элементы локальных матриц «внедряются» в глобальные матрицы. Эффективным с вычислительной точки зрения способом формирования матрицы жесткости является метод ее прямого построения.

В этом случае на первом этапе формируются (например, в результате применения метода Б-Г) локальные системы уравнений для каждого конечного элемента. Далее выполняется процедура

1 Далее будут описаны шаги по формированию матрицы жесткости, построение матрицы нагрузок выполняется аналогично, «синхронно» с матрицей жесткости.

2

включения конечных элементов. Для этого строкам и столбцам локальной матрицы жесткости конечного элемента приписывают номера глобальных степеней свободы. Порядок расположения степеней свободы соответствует обходу элемента против часовой стрелки, начиная от некоторого i- го узла. В частном случае одномерной задачи, где каждый элемент включает по два узла с одной степенью свободы, этот шаг сильно упрощается. Приписывание столбцам и строкам локальной матрицы номеров глобальных степеней свободы позволяет определить, какое место займут коэффициенты в глобальной матрице жесткости. При этом, если одной позиции в глобальной матрице соответствуют элементы в нескольких различных локальных матрицах, то эти элементы складываются между собой.

После завершения процедуры включения полученная глобальная система уравнений должна быть преобразована, если некоторые элементы искомого вектора [ ] известны (заданы). Ситуация, когда часть искомых узловых значений функции заранее известна, является скорее правилом, чем исключением. Например, если решается задача деформации упругого тела под действием приложенных нагрузок, перемещения в отдельных узлах должны быть ограничены для того, чтобы исключить перемещение всего тела (см. рис. 0). Преобразование системы уравнений, соответствующее фиксации некоторого узлового значения представляет собой двушаговую процедуру. Пусть, например, известно значение 5, тогда:

1.Все коэффициенты 5-й строки, за исключением диагонального, приравниваются нулю;

диагональный член остается неизменным: K5 j 0 при j 1,..., n и j 5 . Соответствующий элемент вектора нагрузок [F] заменяется на произведение K55 5 .

2.Все остальные уравнения преобразуются вычитанием произведения K j5 5 из Fj и

Пример решения задачи

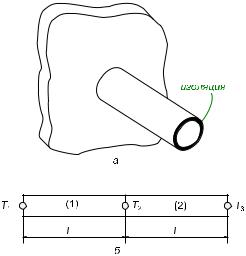
Рассматривается задача о переносе тепла в стержне с теплоизолированной боковой поверхностью (рисунок 1, а). К закрепленному в стене концу стержня подводится тепловой поток заданной интенсивности q. На свободном конце стержня происходит рассеивание тепла (теплообмен), характеризуемое коэффициентом теплообмена h, температурой окружающей среды T . Потери тепла через боковую поверхность стержня отсутствуют. Площадь поперечного сечения A постоянна. Необходимо определить значение температуры в точках x=0, x=2, x=5.

Числовые данные следующие: Kxx = 75 Вт/(см С),

h = 10 Вт/(см2 С)

A = см2,

L = 7.5 см,

q = -150 Вт/см2

Дифференциальное уравнение для распределения температуры вдоль стержня:

с граничными условиями

(4)Kxx dTdx q 0 при x 0,

Kxx dTdx h(T T ) 0 при x L* ,

где Kxx – коэффициент теплопроводности материала стержня, L* – длина стержня.

3

Рисунок 1 – К задаче о переносе тепла

Дискретизация области. Стержень представим в виде совокупности двух одномерных симплекс-элементов (рисунок 1, б) одинаковой длины L. Очевидно, что принадлежность узлов элементам будет следующей:

элемент 1: i=1, j=2; элемент 2: i=2, j=3.

Локальные системы координат каждого узла имеют начало в i-м узле.

Формирование уравнения метода Б-Г. Применение метода Б-Г к уравнению (3) приводит к соотношению

Так как интерполяционная функция T определена на отдельном элементе, уравнение (5) записывается в виде суммы интегралов, задаваемых для каждого e-го элемента:

где R – число элементов, L(e) – длина e-го элемента.

Интерполирующие функции элементов. Выберем функции формы [N (e) ] . Так как в качестве

конечных элементов будут использованы одномерные симплекс-элементы, функция, определяющая элемент, запишется в виде

Вычисление интеграла. Для вычисления интеграла (6) необходимо применить интегрирование по частям, т.к. он содержит производную, порядок которой более чем на единицу превышает порядок непрерывности искомой функции T. Таким образом, получим

4

При преобразовании данного соотношения для каждого элемента необходимо будет подставить вместо первой производной функции T соответствующее выражение, полученное из краевых условий (4). Так, для первого элемента получим:

вычислении она принимается равной нулю (т.е. не учитывается). Аналогично получим выражение для второго элемента (границы интегрирования выражены, как и для первого элемента, в локальной системе координат, однако следует иметь в виду, что верхняя граница интегрирования для второго

элемента соответствует в глобальной системе координат x L* ):

Теперь вычислим интеграл, входящий в (7):

При вычислении интеграла индекс (e) был отброшен, т.к. рассматривался отдельный элемент длиной L, а функции формы выражены в локальной системе координат с началом в i-м узле.

Формирование локальных матриц жесткости и нагрузок для элементов. Выполним подстановку числовых данных и сформируем окончательно локальные системы уравнений для каждого элемента.

Для первого элемента имеем:

5

Для второго элемента имеем:

Формирование глобальных матриц и вычисление узловых значений. Выполним процедуру прямого формирования глобальных матриц жесткости [K] и нагрузки [F]. Матрица жесткости будет иметь размеры 3 3, т.к. имеется три узла с одной степенью свободы каждый (матрица нагрузок, соответственно будет иметь размеры 3 1).

Включаем первый элемент:

Теперь включим второй элемент:

Сформированная общая система уравнений для узловых значений функции принимает вид

Ее решением является вектор узловых значений

6

Вычисление приближенных значений функции в требуемых точках. Теперь определим температуру в требуемых точках. Первая точка совпадает с первым узлом, так что значение температуры в ней известно: T(0) = 70 С. Вторая точка x=2 принадлежит первому элементу, поэтому вычислим температуру, используя его определяющую функцию:

Аналогично определим третью точку, принадлежащую второму элементу. В локальной системе координат элемента координата точки равна (5 7.5 / 2) , то есть 1.25. Таким образом

Задача решена.

Индивидуальные варианты заданий

Задача 1.

Рассматривается задача о переносе тепла в стержне постоянного круглого сечения длиной L, боковые стенки которого имеют частичную теплоизоляцию. Один конец стержня закреплен в стене, и к нему подводится тепловой поток интенсивности q. На свободном торце стержня и через боковые стенки происходит конвективный теплообмен, характеризуемый коэффициентами теплообмена h1 (для боковой поверхности) и h (для свободного торца). Температура окружающей

среды T .

Уравнение для распределения температуры внутри стержня имеет вид

K xx d 2T 2h1 (T T ) 0 dx2 R

с граничными условиями

где Kxx – коэффициент теплопроводности материала стержня, R – радиус стержня. Необходимо определить значения температуры в точках x1=0.15L, x2=0.45L, x3=0.75L.

Разбиение области осуществлять, используя указанное в таблице количество конечных симплекс-элементов (разбиение осуществляется на одинаковые по длине элементы):

7

Задача 2.

Рассматривается задача о переносе тепла в стержне постоянного круглого сечения длиной L, через боковые стенки которого происходит конвективный теплообмен с окружающей средой, характеризуемый коэффициентом h. Один конец стержня закреплен в стене, и к нему подводится тепловой поток интенсивности q. Свободный торец стержня теплоизолирован, теплообмен через поверхность торца не происходит. Температура окружающей среды T .

Уравнение для распределения температуры внутри стержня имеет вид

K xx d 2T 2h1 (T T ) 0 dx2 R

с граничными условиями

где Kxx – коэффициент теплопроводности материала стержня, R – радиус стержня. Необходимо определить значения температуры в точках x1=0.25L, x2=0.55L, x3=0.8L.

Разбиение области осуществлять, используя указанное в таблице количество конечных симплекс-элементов (разбиение осуществляется на одинаковые по длине элементы):

8

Задача 3.

Рассматривается задача о переносе тепла в коническом стержне постоянного круглого сечения длиной L, боковые стенки которого теплоизолированы. Один конец стержня закреплен в стене, и к нему подводится тепловой поток интенсивности q. На свободном торце стержня происходит конвективный теплообмен, характеризуемый коэффициентом теплообмена h. Теплообмен через боковые стенки не происходит. Температура окружающей среды T . Радиус закрепленного основания R1, радиус свободного торца R2.

Уравнение для распределения температуры внутри стержня имеет вид

с граничными условиями

где Kxx – коэффициент теплопроводности материала стержня, S – переменная площадь поперечного сечения стержня, выражается функцией

Необходимо определить значения температуры в точках x1=0.12L, x2=0.5L, x3=0.8L.

Разбиение области осуществлять, используя указанное в таблице количество конечных симплекс-элементов (разбиение осуществляется на одинаковые по длине элементы):

9

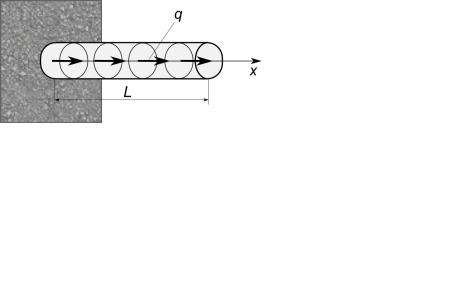
Задача 4.

Рассматривается задача о растяжении стержня длины L, находящегося под действием нагрузки q, распределенной вдоль его оси (см. рисунок). Один конец стержня закреплен неподвижно. Деформация такого стержня описывается дифференциальным уравнением, заданным в перемещениях точек стержня u

где E – модуль упругости материала стержня, F – площадь поперечного сечения стержня. Предполагается, что

EF const .

Необходимо определить величину перемещения незакрепленного конца стержня u(L) и деформацию стержня в конечной его точке x(L).

10