книги / Численные методы решения задач строительства. Ч. 2

где р – заданная явно функция точки; а п – нормаль к S.

Граничными условиями третьего рода (Коши) называются условия, в которых зависимая переменная и ее нормальная производная связаны на границе зависимостью вида

где р и q – известные функции точки на границе S.

Таким образом, рассмотренные граничные условия включают зависимую переменную и (или) ее первую произ-

водную. Таких граничных условий для задачи, описываемой уравнением (8.17), должно быть два: для частей границы S1 и S2. Объединение S1 иS2 образуетполную границу.

Исходное дифференциальное уравнение вместе с краевыми условиями (как и в случае обыкновенных дифференциальных уравнений) называется краевой задачей и представляет собой математическую модель исследуемого объекта или процесса.

Для квазигармонического уравнения (8.17) с гранич-

ными условиями на границе S1 первого рода (8.27) и условиями на границе S2 второго или третьего рода

где полная граница S состоит из суммы S1 + S2; lx, ly, lz – направляющие косинусы единичной внешней нормали n к границе S.

Функционал, связанный с этой краевой задачей, имеет вид

51

В вариационной формулировке граничные условия условно подразделяются на главные и естественные.

Граничные условия первого рода являются главными

граничными условиями и должны быть учтены при конструировании области определения функционала. Граничные

условия второго или третьего рода являются естествен-

ными граничными условиями и в решении удовлетворяются автоматически.

Аналитическое решение большинства практических задач, описываемых дифференциальными уравнениями в частных производных, с помощью аналитических методов весьма проблематично. В основном решение их полу-

чают численными методами.

Выбор численного метода определяет тип дифференци-

ального уравнения и вид дополнительных условий. Чаще все-

го для решения краевых задач, математическим описанием которых являются дифференциальные уравнения в частных производных, применяют методконечных элементов.

Контрольные вопросы

1.Основные понятия вариационного исчисления. Вариационный подход к решению краевой задачи.

2.Связь решения краевой задачи с нахождением минимума функционала

3.Метод Ритца для приближенного решения вариационной задачи.

4.Дифференциальные уравнения в частных производных в строительных расчетах.

52

ГЛАВА 9

Основыметодаконечных элементов

Метод конечных элементов (МКЭ) появился в строительной механике в 1950-х годах, когда появились большие ЭВМ, и в дальнейшем развивался весьма интенсивно. В настоящее время этот метод является одним из наиболее эффективных методов решения краевых задач. Область применения его очень обширна и охватывает практически все физические задачи, которые могут быть описаны дифференциальными уравнениями, как обыкновенными, так и в частных производных.

Это задачи механики деформируемого твердого те-

ла, к которым относятся: задачи строительной механики стержневых систем, задачи теории пластин и оболочек, задачи теории упругости, анализ нелинейного поведения материалов и др.

Это стационарные и нестационарные задачи теории поля: задачи распространения тепла, задачи течения жидкости, газа.

Многие этапы МКЭ являются общими для большинства областей приложения, что позволяет составлять достаточно общие программы.

МКЭ можно применять к расчету конструкций, со-

ставленных из нескольких материалов. Размеры области, границы и нагрузки при этом могут быть любыми.

В настоящее время существует большое разнообразие в формулировках МКЭ (метод Галеркина, метод наименьших квадратов, метод глобального баланса и др.). Классический подход – вариационная формулировка метода, в соответст-

вии с которой минимизируется функционал, связанный с физическим смыслом решаемой задачи. В задачах механики

53

деформируемого твердого тела используются следующие вариационные принципы: принцип Лагранжа, в соответствии с которым варьируются перемещения; принцип Кас-

тильяно (варьируются напряжения), принцип Рейсснера

(варьируются перемещения и напряжения) и др.

В данном учебном пособии основное внимание уделено

методу конечных элементов в форме метода перемеще-

ний, и тогда МКЭ можно рассматривать как один из вари-

антов метода Ритца, в котором используются специфические локальные координатные функции. Выбор и реализа-

ция именно этой формы в большинстве расчетных программных комплексов объясняется простотой алгоритмизации и физической интерпретации, наличием единых методов построения матриц жесткости, векторов нагрузок для различного типа конечных элементов, возможностью учета произвольных граничных условий и сложной геометрии рассчитываемой конструкции.

Подготовка бакалавров по профилю «Промышленное и гражданское строительство» предусматриваеткомпетенции:

–в области изыскательской и проектно-конструк-

торской деятельности – по расчету и конструированию деталей и узлов с использованием стандартных средств автоматизации проектирования;

–в области экспериментально-исследовательской дея-

тельности – по использованию стандартных пакетов автоматизации проектирования и исследований.

Поэтому мы ограничимся теорией и описанием практической реализации задач строительной механики стержневых систем и плоских задач теории упругости на базе специализированных промышленных конечно-элементных программных комплексов типа «ЛИРА» и SCAD.

«От расчетчика – пользователя программных комплексов, интересующегося напряженно-деформированным состоянием, не требуется детального знания всех математиче-

54

ских, вычислительных и компьютерных проблем. Однако ему необходимо иметь представление о том, как математически формулируются задачи и что представляют собой численные методы их решения. Без этого трудно рационально выбрать расчетную схему и правильно оценить достоверность окончательных результатов» [20].

При решении технической или инженерной задачи выполняется переход от исходной физической системы к математической модели. Данный процесс называется идеализацией, поскольку математическая модель абстрагируется от физической реальности. Очевидно, специалист при реализации данного этапа должен обладать специальными теоретическими знаниями, чтобы правильно выбрать соответствующую математическую модель системы (конструкции), которую ему необходимо исследовать.

Идеализация при расчете любой строительной конструкции начинается с построения ее расчетной схемы, встречающейся в учебниках по строительной механике и сопротивлению материалов [7], т.е. с попытки установить, что именно в рассматриваемом случае является существенным, а чем можно пренебречь. Этот этап не относится непосредственно к реализации МКЭ, но является весьма важным для получения достоверных результатов.

При создании расчетной схемы отображается геомет-

рия системы, условия закрепления, принимается решение о размерности задачи (одномерная, плоская или пространственная); о том, какой расчет будет выполняться: линейный или нелинейный; следует ли учитывать силы инерции и выполнять динамический расчет или можно ограничить-

ся статическим анализом.

После того как расчетная схема установлена, наступает период ее детального описания в форме, пригодной для выполнения расчетногоанализа методом конечных элементов.

55

9.1. Основные теоретические положения метода конечных элементов

Математическая сущность подхода к расчету конст-

рукций на основе идеализации континуальной среды дискретными элементами, называемого методом конечных эле-

ментов, обоснована заменой системы дифференциальных уравнений (краевой задачи) – системой алгебраических урав-

нений, имеющих каноническуюформу, которую в матричном виде можно записать так:

Здесь К – матрица коэффициентов системы, зависящая от

параметров описания системы (ее принято называть матрицей жесткости); – вектор неизвестных узловых значе-

ний искомой функции (перемещения узлов); F – вектор

внешней нагрузки.

Будем рассматривать решение линейных краевых задач МКЭ в форме метода перемещений, в котором исполь-

зуется вариационный принцип возможных перемещений Лагранжа.

Вид функционала – потенциальной энергии системы, связанного с краевой задачей определения напряженно- деформиро-ванного состояния конструкций, зависит от типа конструкции (стержневая, пластинчатая, массивное тело), размерности задачи, принятых постулатов, гипотез. Ниже приведены некоторые выражения для потенциальной энергии:

– стержневой системы

56

– двумерного случая (плоской задачи теорииупругости)

Процесс минимизации функционала и приводит к сис-

теме линейных алгебраических уравнений (9.1) относительно неизвестных узловых значений искомой функции, которая представляет собой разрешающиеуравненияМКЭ.

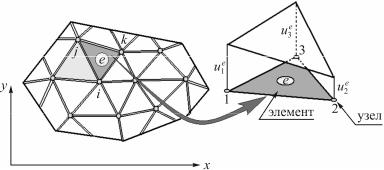
Порядок системы линейных алгебраических уравнений (9.1) определяется числом степеней свободы расчетной модели. Применительно к методу перемещений ими являются все возможные перемещения точек или сечений, называемых узлами, перемещения которых однозначно определяют расчетное деформированное и напряженное состояние системы. Это достигается нанесением сетки на расчетную область, которая расчленяет континуальную среду на элементы (рис. 9.1), имеющие конечные размеры и конечное число степеней свободы. Конечные элементы (КЭ) соединяются между собой в точкахили по линиям.

Рис. 9.1. Разбиение области на КЭ [14]

На полученной дискретной модели вводится система кусочно-непрерывных функций i (x) , определяемых на

57

каждом конечном элементе. Эти функции называют аппроксимирующими, координатными или базисными.

 Под конечным элементом принято понимать малую область тела в совокупности с заданными в ней аппроксимирующими функциями.

В качестве аппроксимирующих функций элементов чаще всего используются полиномы, которые подбираются так, чтобы обеспечить непрерывность искомой функции в узлах на границах элементов.

Выбор аппроксимирующих функций зависит от физи-

ческого смысла конкретной задачи, геометрической формы элемента и числа узлов в элементе. В задачах статиче-

ского расчета конструкций исходя из принципа виртуальной работы аппроксимирующие функции описывают возможное поле перемещений (линейных и угловых).

9.2. Общая схема решения задач методом конечных элементов

Рассмотрим основные этапы решения задач МКЭ, выделив основные математические формулировки и особенности МКЭ, которые должен понимать расчетчик – пользователь программных комплексов.

1.Дискретизация расчетной схемы.

2.Аппроксимация искомой функции на каждом конечном элементе полиномом.

3.Составление разрешающих уравнений МКЭ – системы линейных алгебраических уравнений.

4.Решение системы линейных алгебраических уравнений и определение значений неизвестных перемещений в узлах сетки.

5.Определение компонентов напряженно-деформиро- ванного состояния (перемещений, внутренних усилий, напряжений) вобласти элементов и всейсистемы.

58

9.2.1. Дискретизация расчетной схемы

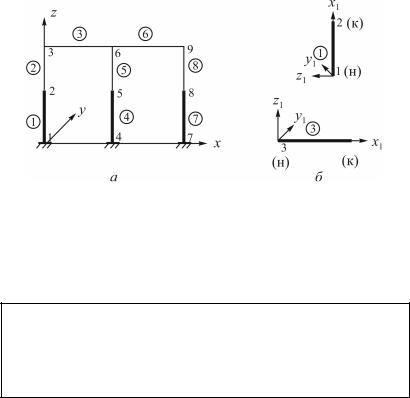
Дискретизация расчетной схемы – это замена континуальной среды совокупностью конечных элементов (КЭ) заданной формы, соединенных между собой в узлах конечным числом связей. На рис. 9.2 показан пример дискретизации расчетной схемы плоской рамы.

Множество элементов, на которые разбита конструк-

ция, называется конечно-элементной сеткой.

Рис. 9.2. Дискретизация расчетной схемы плоской рамы:

а– глобальная; б – локальная системы координат

Вдополнение к общепринятому содержанию понятия расчетной схемы введем понятие расчетной модели системы.

Расчетной моделью системы (конструкции) будем называть совокупность отдельных конструктивных элементов, соединенных конечным числом шарнирных и жестких узлов и нагруженных внешней нагрузкой (это могут быть силы, перемещения, температура и др.).

Это определение полностью соответствует расчетной схеме стержневых систем. Для более сложных конструктивных элементов (пластины, оболочки, массивные тела)

59

оно также подходит, только при этом усложняется математический аппарат.

Конечные элементы представляют собой топологически изученные геометрические фигуры: отрезки, треугольники и прямоугольники, параллелепипеды и тетраэдры

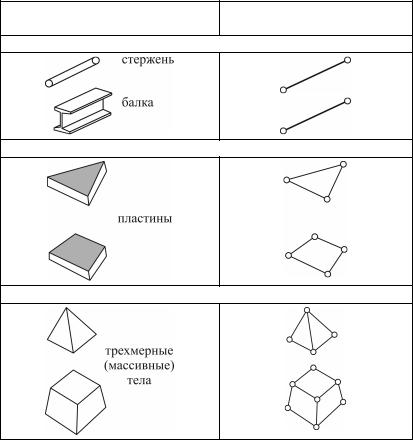
идр. В расчетной модели они сопрягаются общими узлами. Наиболее очевидная классификация конечных элементов – по геометрической форме: одномерные, двумерные

итрехмерные КЭ (рис. 9.3).

Двумерные

Трехмерные

Рис. 9.3. Классификацияэлементовпогеометрической форме[16]

60