
книги / Теория электропривода.-1
.pdfОтдельные элементы электропривода содержат различные накопители электрической, электромагнитной, тепловой
имеханической энергии, а также различные преобразователи энергии (трансформаторы, электромеханические генераторы, вентильные преобразователи), связанные между собой механическими, электрическими или магнитными связями. Электрическая и механическая части электропривода находятся в постоянном взаимодействии с непрерывным преобразованием энергии и передаче ее из одного накопителя в другой.
Механическая часть электропривода может иметь многомассовую структуру с упруговязкими механическими элементами, например с длинными валами или канатами, связывающими движущиеся массы с постоянными моментами инерции. В некоторых механизмах (например, в экскаваторах, транспортерах) величина движущейся массы (или момент инерции) меняется в процессе движения. Наконец, есть электроприводы, у которых передаточное устройство между двигателем и рабочей машиной имеет меняющееся передаточное число (например, у кривошипно-шатунных механизмов), что влияет на расчетное значение момента инерции
идинамического момента на валу двигателя.
Всоответствии с законом Ньютона задачи механики электропривода решаются для вращательного и поступательного движений как
± M ± Mc = Mj, |
(2.1) |
± F ± Fc = Fj, |
(2.2) |
где М, F – развиваемые в электродвигательном устройстве моменты (силы);
Мс, Fс – статические моменты (силы) сопротивления движению, создаваемые в рабочей машине и передаточном устройстве;
Mj, Fj – динамические моменты (усилия), определяющие характер и направление движения электропривода.
21
Для любых типов электродвигательных устройств электропривода движущий момент (сила) определяется значением нагрузки на его валу, т.е. моментом сопротивления Mс (усилия) в установившихся и переходных режимах работы электропривода.
2.2.Классификация статических моментов
исил сопротивления движению
При рассмотрении работы электропривода производственного механизма необходимо, прежде всего, выявить соответствие механических свойств электродвигателя и производственного механизма, изучить их механические характеристики.
Момент нагрузки на валу рабочей машины (момент сопротивления движению) создается различными силами полезных и вредных сопротивлений. Эти моменты сопротивления классифицируются по характеру сил сопротивления движению или по конструкции рабочей машины и особенностям технологического процесса.
По характеру сил сопротивления движению все мо-
менты статического сопротивления делятся на две группы:
Реактивные моменты сопротивления – это моменты,
создаваемые силами трения или силами неупругих деформаций – растяжения, сжатия, скручивания или изгиба неупругих тел (силами реакции), и всегда направленные против движения, как показано на рис. 2.1, а (Mc = const). Поэтому характеристика реактивного Мс имеет разрыв непрерывности при изменении знака направления движения (скорости ω). Направления Мс против движения учитываются знаком (–) перед величиной этого момента в уравнении движе-
ния (2.1).
22

а |
б |
|
Рис. 2.1. Моменты сопротивления: |
Рис. 2.2. Разновидности |
|
а – реактивный; б – активный |
рабочих машин по момен- |
|
|
|
там сопротивления |
Активные (потенциальные) моменты сопротивления –
это моменты, создаваемые силой тяжести или силами упругих деформаций (сжатие, скручивание, растяжение). Активные моменты сопротивления называются также потенциальными, так как они являются мерой измерения запаса потенциальной энергии движущихся масс или упруго-деформируе- мых элементов машин. Примерами активного Мс являются, например, момент сопротивления, возникающий при упругой деформации пружины, момент сопротивления груза в подъемной установке. Активные моменты сопротивления могут быть направлены по движению или против него, т.е. могут быть положительными или отрицательными. Например, в уравнении движения (2.1) знак активного момента перед Mс при изменении направления движения не меняется, как показано на рис. 2.1, б, для механизмов, в которых момент сопротивления создается массой груза, подвешенного на барабане лебедки подъемника.
Все рабочие машины с точки зрения моментов сопро-
тивления движению по их конструкции и особенностям технологического процесса можно разбить на несколько групп, для которых механическая характеристика механизма может быть представлена как зависимость момента сопротивления Мс от различных факторов. Для ряда механизмов таким определяющим фактором является скорость движения
23

рабочего органа. В этом случае зависимость Мс = f(ω) может быть представлена математически следующим образом:
х
Mс = M0 +(Mс.н − M0 ) ωω , (2.3)
н
где М0 – момент трения в движущихся частях механизма; Мс.н – момент сопротивления при номинальной скоро-
сти ωн;
х– показатель степени.
На рис. 2.2 приведены возможные механические характеристики рабочих машин Мс = f(ω) при реальных значениях х:
– Независимая от скорости (постоянный момент) (х = 0),
Mс = Mс.н = const. Такой механической характеристикой обладают рабочие машины, преодолевающие трение (прокатные станы, бумагоделательные машины и др.), совершающие подъем грузов. Мощность в таких рабочих машинах с ростом скорости изменяется линейно, т.е. P = Мω.
– Линейная характеристика (х = 1), Mс = M0 +
|
|
|
|
|
ω |
|
||
+(M |
с.н |
− M |
0 |
) |
|
|
, т.е. момент растет линейно, а мощность |
|
ω |
||||||||
|
|
|
|
|
||||
|
|
|
|
н |
|
|||
квадратично со скоростью. Примером такой характеристики является привод генератора постоянного тока с независимым возбуждением, работающего на внешнюю постоянную электрическую нагрузку.
– Квадратичная |
характеристика (х = 2), Mс = M0 + |
|||||||
|
|
|
|
|
ω 2 |
|
||
+(M |
с.н |
− M |
0 |
) |
|
. |
В этом случае момент сопротивления |
|
ω |
||||||||
|
|
|
|
|
||||
|
|
|
|
н |
|
|||
пропорционален квадрату скорости, а мощность – скорости в 3-й степени. Такую механическую характеристику, называемую вентиляторной, имеют механизмы, преодолевающие
24

сопротивление воздуха, газа или жидкости (вентиляторы, центрифуги, центробежные насосы, дымососы, судовые гребные винты и т.п.).
– Нелинейно-спадающая (гиперболическая) характери-
−1
стика (х = –1) и M = M +(M − M ) ω , т.е. момент
с 0 с.н 0 ω
н
сопротивления обратно пропорционален скорости, мощность примерно постоянна. Такая характеристика у некоторых токарных и расточных станков, моталок кабельной продукции и др.
Кроме указанных механических характеристик, у которых момент сопротивления зависит от скорости рабочей машины, имеются механизмы, определяющие зависимость Мс от других факторов:
– Механическая характеристика с зависимостью момента сопротивления от пути, пройденного рабочим орга-
ном. В этом случае Мс = f(S) или Мс = f(α), где S и α – соответственно линейное или угловое перемещение рабочего
органа. Примером таких механизмов является шахтный подъемник с неуравновешенным канатом (при больших глубинах шахт масса каната значительно превышает суммарную массу скипа и полезного груза), механизмы с кривошипношатунной передачей (например, ножницы гильотинного типа для резки металлов, поршневые насосы и компрессоры).
– Механическая характеристика с зависимостью от случайных величин, когда изменение момента сопротивления определяется случайными факторами (например, появлениями вкраплений породы различной прочности, сказывающейся на нагрузке буровой установки, дробилки, ковша экскаватора). Момент сопротивления у таких рабочих машин определяется по статистическим данным.
25
2.3. Механические характеристики электродвигателей
Механическая характеристика электродвигателя определяет зависимость его скорости ω от развиваемого им момента M. Часто вместо угловой скорости ω используют внесистемную физическую величину – частоту вращения n, так как эти величины пропорциональны:
ω= |
2πn |
. |
(2.4) |
|
60 |
||||
|
|
|
В этом случае механической характеристикой электродвигателя называется зависимость частоты вращения n от развиваемого им момента M, т.е. n = f(M). Степень изменения скорости с изменением момента у различных типов электрических машин неодинакова и различается в зависимости от жесткости механических характеристик (рис. 2.3).
Под жесткостью механической характеристики β понимается отношение приращения момента ∆M к приращению скорости двигателя ∆ω:
β = |
M1 |
− M2 |
= |
∆M |
, |
(2.5) |
|
ω |
−ω |
∆ω |
|||||
|
|
|
|
||||
|
1 |
2 |
|
|
|
|
где M1, M2, ω1, ω2 – моменты и угловые скорости соответственно в первой и второй точках механической характеристики.
Механические характеристики электродвигателей можно разделить на четыре основных типа, приведенных на рис. 2.4, в зависимости от жесткости β:
1) абсолютно жесткая механическая характеристика, при которой скорость с изменением момента остается неизменной. Из (2.5) следует, что если ∆ω = 0, то β = ∞. Такой характеристикой обладают синхронные двигатели (прямая 1);
2) жесткая механическая характеристика, отличающаяся незначительным изменением угловой скорости с изменением момента. Жесткой механической характеристикой обладают
26

Рис. 2.3. Определение жесткости |
Рис. 2.4. Механические |
механической характеристики |
характеристики |
электродвигателей |
|
асинхронные двигатели (кривая 2) и двигатели постоянного тока независимого и параллельного возбуждения (прямая 4); 3) мягкая механическая характеристика отличается значительным изменением угловой скорости с изменением момента. Такой характеристикой обладают двигатели постоянного тока последовательного возбуждения (кривая 3) и двигатели постоянного тока смешанного возбуждения (кри-
вая 5); 4) абсолютно мягкая механическая характеристика, при
которой момент двигателя остается неизменным с изменением угловой скорости. Если ∆M = 0, то из (2.5) следует, что β = 0. Абсолютно мягкой механической характеристикой обладают двигатели постоянного тока независимого возбуждения при питании обмотки якоря от источника тока (прямая 6).
2.4. Статическая устойчивость механического движения
Установившийся режим работы электропривода cоответствует равенству момента, развиваемого электродвигателем, и момента сопротивления на его валу. Данный режим на рис. 2.5 обозначен точкой А пересечения механических ха-
27

|
рактеристик |
двигателя |
1 и |
|
механизма 2 и характеризу- |
||
|
ется отсутствием динамиче- |
||
|
ского момента. |
|
|
|
При |
положительном |
|
|
приращении |
скорости |
вра- |
|
щения двигателя от устано- |
||
|
вившегося |
значения |
вра- |
Рис. 2.5. К определению статиче- |
щающий момент двигателя |
||
уменьшится |
до Mд1, а мо- |
||
ской устойчивости механического |
мент сопротивления меха- |
||
движения |
низма возрастет до Мс1. Воз- |
||
|
|||
никает отрицательный динамический момент, вызывающий торможение электропривода до значения скорости вращения в т. А. Если скорость вращения от установившегося значения получает отрицательное приращение, например до ω2, из-за превышения момента двигателя над моментом сопротивления положительный динамический момент разгоняет привод до прежнего значения. Таким образом, в т. А статический режим электропривода является устойчивым.
Условие устойчивости является необходимым условием работоспособности электропривода.
Статическая устойчивость электропривода при известных аналитических уравнениях механических характеристик электродвигателя и производственного механизма легко оп-
ределяется по уравнению |
|
β – βc < 0, |
(2.6) |
где β и βс – соответственно статические жесткости механических характеристик двигателя и производственного механизма, приведенные к валу двигателя.
Для сложных механических характеристик, например у асинхронного электродвигателя, приведенного на рис. 2.6, могут существовать два режима, определяющих равенство
28
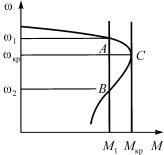
момента движения M и момента сопротивления Mc, соответствующих точкам А и В. Несложно определить, что в точке А условия устойчивости выполняются, а в точке В нет.
Более того, при увеличении момента сопротивления механизма параметры устойчивого статического режима могут принять значения, соответствующие точке С. Режим в дан-
ной точке называют критическим, при увеличении момента сопротивления выше Мкр происходит «опрокидывание» электродвигателя и двигатель останавливается в аварийном тормозном режиме.
2.5.Приведение статических моментов, усилий, моментов инерции и движущихся масс к одному движению
2.5.1. Общие принципы решения задач приведения
Механическая часть электромеханической системы электропривода представляет собой сложную систему, включающую связанные движущиеся массы: двигателя, передаточного устройства и исполнительного механизма машины. Непосредственное представление о движущихся массах установки и механических связях между ними дает кинематическая схема электропривода. В кинематической схеме различные элементы системы движутся с разными скоростями, поэтому непосредственно сопоставлять их моменты инерции Ji, массы mj, нельзя. В связи с этим одной из первых задач проектирования и исследования электроприводов является составление упрощенных расчетных схем механической части.
29
Задача может быть решена просто, если реальная система «двигатель – передача – рабочая машина» заменяется некоторой эквивалентной системой, движущейся с одной скоростью (обычно это скорость двигателя ω) и описываемой лишь одним уравнением движения.
Эквивалентная система с приведенными значениями параметров должна обладать теми же статическими и динамическими свойствами, что и реальная система. При инженерных расчетах механические связи можно принять абсолютно жесткими (не учитывать упругость звеньев и наличие зазоров в передачах). Тогда движение одного элемента дает полную информацию о движении всех остальных элементов, и достаточно рассматривать один элемент. В качестве такого элемента обычно принимают вал двигателя.
Таким образом, чтобы решить задачу приведения, надо составить уравнения баланса кинетических энергий, мощностей для реальной и эквивалентной систем c учетом потерь мощности в системе.
Задача приведения показана на примерах систем электропривода с вращательным и поступательным движениями механизмов (рис. 2.7, а, б).
На рис. 2.7 приняты следующие обозначения:
Jд, J1, Jм, Jб – моменты инерции двигателя и деталей на его валу, деталей на промежуточном валу, рабочей машины и барабана;
ω, ω1, ωб – скорости вращения двигателя, промежуточного вала и рабочей машины;
i1, i2, η1, η2 – передаточные числа ступеней передач и их КПД;
ηб – КПД рабочей машины;
Mс, Mс.м – приведенный к валу двигателя момент сопротивления, момент сопротивления рабочей машины;
mг, Vм, Fс.м – масса груза, линейная скорость перемещения и сила сопротивления рабочей машины.
30
