Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пермский национальный исследовательский политехнический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

книги / Теория механизмов и машин. Ч. 1

.pdf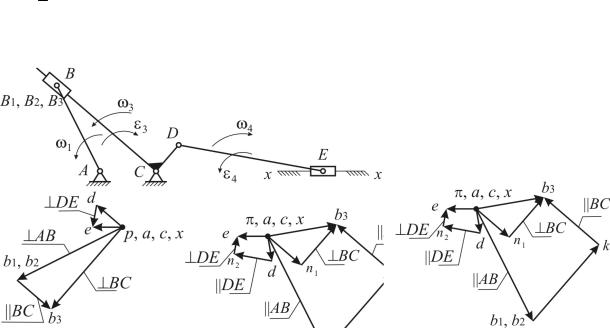

Скачиваний:

Добавлен:

12.11.2023

Размер:

7.74 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 146 7 8 9 10 11 12 13 14 > Следующая >>>

в)

VB3

B3B2 , VB3B2 BC ,

VB3

VB2

V V

, V

B3C B3C

pb3 V ; VB V pb3

; VB B

b2 b3 V ; 3

l CB3

а		б

Рис. 4.5. Планы пятизвенного стержневого механизма: а – скоростей; б – ускорений

Построения в соответствии с этапом в) представлены на рис. 4.5, а.

CD pd

CD pb

V pd .

pb3

CB3

При нахождении положения точки d плана скоростей используется пра-

вило обхода контура B3CD и b3cd (см. рис. 4.5, а).

Ex , VEX / / x x ,

г)

, V

ED .

Построения этапа г) изображены на рис. 4.5, а.

V pe

de ;

VED

VED .

; V

lED

Полный план скоростей для механизма представлен рис. 4.5, а.

Построение плана ускорений

а) aA aC aX 0.

б)

aB aB

;

,aB

//AB ,

, b //AB .

lAB

aB aBk

a rB B

2 V

, b k

aB3B2

,a r

//BC ,

B B

в)

B C

a B C ,

VB23

aB C

3lB C

lB3C

aB3C

,a n

//BC;a

BC.

B C

Построения этапа в) проведены на рис. 4.5, б. По результатам этих по-

строений получаем

n b

;

; ar

B3C

B C

1 3

B B

lB C

l B3C

г)

CD d

CD b

d .

CB3

Положение т. d плана ускорений находится по правилу обхода контура

В3СD и b3cd (рис. 4.5, б).

aE aX aExk

a rEx , aExk

2 x VEx 0;aExr //x x ,

д)

На рис. 4.5, б проведены построения этапа д).

e ; a

n e ; ar

;

aED

lED

Планускорениямеханизмавзаданномположенииизображеннарис. 4.5, б.

Контрольные вопросы и упражнения

1.Суть графоаналитического метода кинематического анализа механизмов.

2.Понятие о планах скоростей и ускорений.

3.Порядоксоставлениявекторныхуравненийприкинематическоманализе.

4.Суть метода подобия.

5.Определение угловой скорости и углового ускорения по величине

инаправлению для звеньев механизма.

6.Определение ускорения Кориолиса.

7.Нормальное ускорение: его величина и направление.

8.Особенности и уравнения при построении планов скоростей и ускорений для четырехзвенных плоских механизмов.

9.1 = 100 рад/с, lAB = 0,1 м, lBC = 0,4 м, lCD = 0,35 м. Найти 2 для данно-

го положения.

10.lOA = 0,3 м; OA = 12 с–1. Определить скорость поступательного движения кулисы в данном положении механизма.

11.Определить величину нормального ускорения точки A относительно точки В в данном положении механизма.

lOA = 15 см lAB = 0,3 м ωOA = 20 с–1

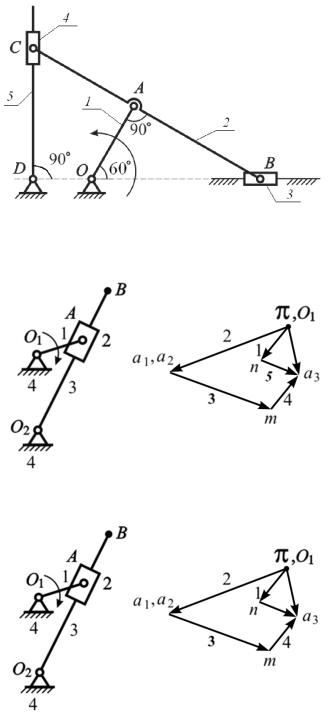
12. Чему равно ускорение Кориолиса аCk5C4 в данном положении механизма?

lOA = 30 см ωAO = 20 с–1

lAB = lAС lCD = 1 м

13. Указать вектор плана, соответствующий тангенциальному ускорению точки А относительно О2.

14. Указать вектор ускорения Кориолиса.

Лекция 5 АНАЛИТИЧЕСКИЙ МЕТОД КИНЕМАТИКИ ПЛОСКИХ РЫЧАЖНЫХ МЕХАНИЗМОВ

Содержание: метод векторных контуров; примеры кинематического исследования плоских рычажных механизмов.

Ключевые слова: векторный контур; уравнение замкнутости; задачи о положениях, скоростях и ускорениях.

5.1. Основные положения метода векторных контуров

Аналитические методы в отличие от графических и графоаналитических позволяют проводить кинематические исследования эффективно, с высокой степенью точности, с использованием численных методов и компьютерных технологий.

Один из методов аналитической кинематики рычажных механизмов метод векторных контуров, предложенный В.А. Зиновьевым.

Звенья механизма представляются в виде векторов, образующих замкнутый контур, уравнения которого проецируются на оси системы координат. На основе полученных математических соотношений решаются задачи о положениях, скоростях и ускорениях.

Для удобства дальнейшего изложения приняты следующие допущения

иобозначения:

1)k и k угловая скорость и угловое ускорение k-го звена;

2)VSk и aSk скорость и ускорение точки S k-го звена;

3)k , k , VS и aS соответственно аналоги угловой скорости и углового ускорения k-го звена, аналоги скорости и ускорения точки S;

4)	k	l	k	;		lAS	2	отношение длин звеньев к длине 1-го звена.

		l1			AS2	l1

Исходные данные для проведения расчетов: длины звеньев, угловая или линейная скорость начального (начальных) звена, схема механизма.

Применение аналитического метода удобно рассмотреть на примерах плоских рычажных механизмов.

5.2. Кинематический анализ кривошипно-ползунного механизма

Случай сборки механизма, когда при обходе по часовой стрелке сохраняется контур с последовательностью OABCO, представлен на рис. 5.1.

Рис. 5.1. Схема кривошипно-ползунного механизма

Даны длины звеньев, угловая скорость 1 и угловое ускорение 1 кривошипа OA.

Задача о положениях

Уравнение замкнутости векторного контура

								0 .				(5.1)
		l1	l2		l3		l4
В проекциях на оси xOy системы координат (рис. 5.1)
l	cos l					cos				l	,	(5.2)
1	1			2					2	4
l1 sin 1				l2 sin 2						e,

так как 3 = 270 , 4 = 180 , l3 e дезаксиал.

Решая второе уравнение из (5.2), получают значение угла 2, характеризующего положение шатуна:

									e sin 1				(5.3)
2 arcsin e l1 sin 1						arcsin			e sin 1			.	(5.3)
				l2					2
Текущее положение ползуна (точка C)
								e sin 1		2
x	l	l	cos		2	1		e sin 1			.
C	4	1		1	2				2
									2

Максимальный ход ползуна
H l4 max l4 min			l1	2 1 2			e2		2 1 2 e2				.

Текущее перемещение ползуна относительно одного из крайних положений, например левого

										e sin 1	2		1 2 2
S		x	l		l	cos			1	e sin 1			1 2 2	.
	C	C		4 min	1		1	2		22		2	e

Задача о скоростях

Дифференцируяпо времени (5.3), определяют угловую скорость шатуна:

		d	sin				cos						cos 1					2	,
			sin			2	cos			2		2	cos 1			2			,
		dt				2				2		2	2	1		2				1
		dt											2
где	cos 1			аналог угловой скорости шатуна.
где				аналог угловой скорости шатуна.
2	2 cos 2
	2 cos 2
Скорость ползуна
		V			dSC			l	sin sin						V					,
		V						l	sin sin						V					,
			C		dt			1			1		1 2 2	2			C		1
					dt

где VC l1 sin 1 2 2 sin 2 .

Задача об ускорениях

2	d	2 1	2	2	sin 1 cos 2 sin 2 cos 1 2 .
2	dt	2 1	2 cos2	2	sin 1 cos 2 sin 2 cos 1 2 .
	2		1

aC dVdtC l1 12 cos 1 2 sin 2 22 1 sin 1 2 2 sin 2 .

Замечание. Для определения кинематических характеристик т. S2 зве-

на AB (см. рис. 5.1)

(5.4)

lAS2 lS2 .

В проекциях на оси координат

xS2

l1 cos 1

lAS2

cos 2 ,

(5.5)

yS2

l1 sin 1

lAS2

sin 2.

Проекции скорости точки S2

sin

1 1

AS2

cos

AS2

cos

1 1

Значение скорости точки S2 и направляющий угол VS2 вектора этой

скорости относительно оси 0x

2 ,

arccos

xS2

VS2

Аналогичным образом находится ускорение точки S2:

xS2 l1 12 cos 1 AS2 22 cos 2 1 sin 1 2 AS2 sin 2 , yS2 l1 12 sin 1 AS2 22 sin 2 1 cos 1 2 AS2 cos 2 ,

aS2 xS22 yS22 , aS2 axS2 .

В некоторых механизмах длина шатуна существенно больше длины кривошипа, т.е. 2<<1. В этом случае для определения кинематических характеристик используют приближенные, более простые формулы на основе разложения радикалов в ряд по формуле бинома Ньютона. Подробнее с этими решениями можно ознакомиться в различных учебниках по ТММ.

5.3. Кинематический анализ шарнирного четырехзвенника

Система координат выбрана так, что ось Ox направлена от точки O к точке C (рис. 5.2).

									Даны длины звеньев, угловая скорость
						1 и угловое ускорение 1 кривошипа OA.
									Уравнение									замкнутого										векторного
						контура OABC
																											.			(5.6)
																	l1			l2				l3		l4	.			(5.6)
									В проекциях на оси координат
Рис. 5.2. Схема шарнирного								l			cos l					cos							l		cos l				,
четырехзвенника								l			cos l					cos							l		cos l				,	(5.7)
четырехзвенника								1					1	2								2	3					3 4		(5.7)
								l1 sin 1						l2 sin 2									l3 sin 3 ,
Задача о положениях						так как 4 = 0.
Задача о положениях
Из OAC длина вспомогательного вектора																	(см. рис. 5.2)
Из OAC длина вспомогательного вектора															l5		(см. рис. 5.2)
l	l2	l2			2l l	cos				l		1 2				2					4		cos .
5	1		4		1 4			1			1			4							4				1
Значения дополнительных углов в соответствии с рис. 5.2
		y	A				sin												2				2		2
		y					sin												2				2		2
arcsin				arcsin						1	,		arccos								2		5		3			,
										1

		l5					5					5											2 2 5
		l5					5																2 2 5
					p arccos			2			2		2
					p arccos					3		5		2 .
											2 3 5

Величины углов поворота звеньев AB и BC:

2		при y	A	0,
	5
	5	при yA 0,
3	p при yA 0,

	p при yA 0.

Задача о скоростях

Дифференцируя соотношения (5.7), получают систему уравнений относительно угловых скоростей звеньев 2 и 3:

sin 1 1 2 2 sin 2				3 3 sin 3		,		(5.8)
				3 3 cos	3.
cos 1 1 2 2 cos 2
В результате решения (5.8)
2 2 1,	2		sin 1 3				,
			2 sin 2 3

3 3 1,	3		sin 1 2			.
		3 sin 2 3

Линейные скорости точек A и B

VA l1 1 , VB l3 3 ,

а их проекции

xA l1 1 sin 1 ; yA l1 1 cos 1 .

xB xA l1 2 2 sin 2 ; yB yA l1 2 2 cos 2 .

Задача об ускорениях

Соотношения для определения угловых ускорений 2-го и 3-го звеньев получают дифференцированием (5.8):

		2	sin 1 1					2			2 2 sin 2									2		3 3 sin 3 ,
cos 1 1			sin 1 1			2 2 cos 2					2 2 sin 2					3 3 cos 3						3 3 sin 3 ,
			cos 2 sin										cos						2 sin							cos .
sin 2			cos 2 sin						2			2	cos		2				2 sin						3	cos .
	1	1		1	1		2	2	2		2	2			2			3		3	3			3	3		3
В результате
						2 2 1							1
						2 2 1				2 sin2 2				3
cos			3	sin	2		3			3	cos			2			3	sin					3				3	;
	1		3		2		3	1		3				2			3				1		3		2		3

									3 3 1				1
									3 3 1			3 sin2 2			3
cos					2	sin		2		3		2	cos		2		3	sin			2		3	.
			1		2			2		3	1	2			2		3		1		2	2	3
Линейные ускорения точек и их проекции
a	A	l	4	2 ;			x	l 2 cos l sin							;	y	l 2 sin l cos								;
	A	1	1			1	A		1 1		1		1 1	1		A		1 1		1		1 1		1
				aB l3			34		32 ; xB xA l1 2 22 cos 2 1 sin 2 ;
							yB yA l1 2 22 sin 2							2 cos 2 .

Значения кинематических характеристик различных точек звеньев определяются аналогично методике, представленной в п. 5.2.

5.4. Кинематический анализ кулисного механизма

Схема механизма с качающейся кулисой представлена на рис. 5.3.

Рис. 5.3. Схема кулисного механизма

Даны длина кривошипа AB, кулисы OC, расстояние OA, угловая скорость 1 и угловое ускорение 1 кривошипа AB.

Уравнение замкнутости векторного контура OABО
l1 l3 l4 0 .	(5.9)

Вектор l3 , характеризующий положение камня кулисы, имеет переменную величину и направление.

Задача о положениях

В проекциях (5.9) на оси координат (см. рис. 5.3)

l	cos	l	cos ,	(5.10)
1	1	3	3	(5.10)
l1 sin 1		l4	l3 sin 3.

<<< < Предыдущая 1 2 3 4 56 / 146 7 8 9 10 11 12 13 14 > Следующая >>>

Соседние файлы в папке книги

#
12.11.20231.54 Mб2Теория линейных электрических цепей. Ч. 2.pdf
#
13.11.202324.53 Mб11Теория литейных процессов..pdf
#
12.11.202313.07 Mб7Теория механизмов и машин задания, упражнения и задачи к курсовому проекту..pdf
#
12.11.202316.79 Mб5Теория механизмов и машин курсовое проектирование..pdf
#
12.11.20239.05 Mб36Теория механизмов и машин сборник задач и тестов..pdf
#
12.11.20237.74 Mб5Теория механизмов и машин. Ч. 1.pdf
#
12.11.20235.9 Mб3Теория механизмов и машин..pdf
#
20.11.202347.33 Mб5Теория механизмов и механика машин.-1.pdf
#
12.11.20238.44 Mб4Теория механизмов и механика машин..pdf
#
19.11.202332.51 Mб4Теория механизмов и механика систем машин в задачах и решениях..pdf
#
12.11.202320.05 Mб11Теория механизмов и механика систем машин..pdf