Лабораторная работа №5 Изучение временных и спектральных характеристик колебательных контуров

Список условных обозначений

- мгновенное значение электрического сигнала,

- комплексная амплитуда гармонического сигнала,

- угловая частота гармонического сигнала,

- комплексная передаточная функция цепи,

- функция Хэвисайда,

- функция Дирака,

- переходная временная характеристика цепи,

- импульсная временная характеристика цепи,

- активное сопротивление (резистор),

- индуктивность,

- емкость,

- резонансная частота колебательного контура,

- коэффициент затухания колебательного контура,

- эквивалентное сопротивление колебательного контура,

- коэффициент взаимной индуктивности,

- добротность,

- коэффициент связи в системе колебательных контуров.

Цель работы: Измерение временных характеристик одиночного колебательного контура и системы индуктивно связанных колебательных контуров, определение амплитудно-частотных характеристик этих систем по результатам измерения параметров их временных характеристик.

Темы, знание которых необходимо для выполнения работы:

1. Методы анализа переходных процессов в линейных электронных системах.

2. Основы теории линейных пассивных четырехполюсников.

0. 5.1 Теория

При анализе прохождения сигналов через радиоэлектронные цепи применяются следующие методы решения прямой задачи теории цепей:

а) классический метод, основанный на непосредственном решении дифференциального уравнения, описывающего цепь; б) спектральный (или частотный) метод и тесно связанный с ним операторный метод (преобразования Фурье и преобразования Лапласа); метод временных характеристик (метод интеграла Дюамеля).

а) Частотные и временные характеристики цепи. В основе спектрального метода лежит использование обобщенной передаточной функции цепи , определяемой как отношение комплексной амплитуды отклика системы к комплексной амплитуде воздействия (рис.5.1)

(5.1)

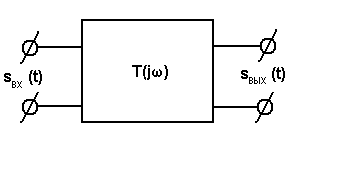
Рис.5.1. К определению функции .

Эта функция, имеющая в общем случае размерность сопротивления и проводимости или безразмерная, полностью определяет свойства четырехполюсника в стационарном режиме при гармоническом воздействии. Ее модуль называетсяамплитудно-частотной характеристикой четырехполюсника, а аргумент - егофазо-частотной характеристикой.

Если представить воздействие и отклик системы в виде интегралов Фурье

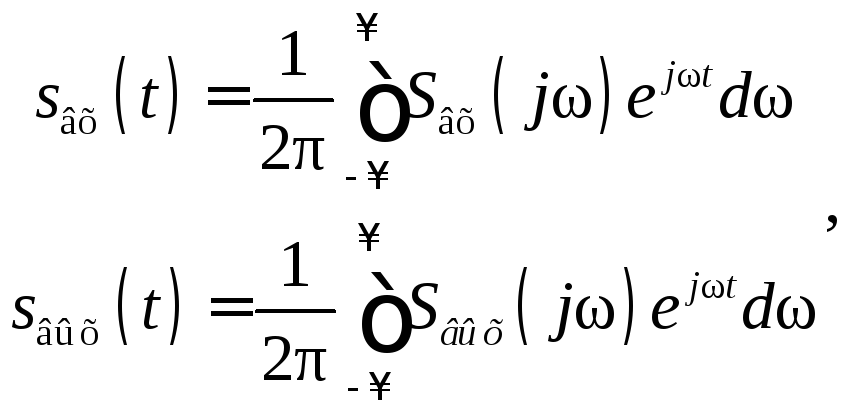(5.2)

то нетрудно получить выражение, связывающее спектральные плотности входного и выходногосигналов через передаточную функцию

(5.3)

В основе метода временных характеристик лежит использование функций времени (импульсная временная характеристика) и (переходная временная характеристика), представляющих собой соответственно отклики системы на воздействия в виде функций - функции Дирака и функции Хэвисайда. Эти две функции являются столь же полными характеристиками свойств системы, что и функцияв спектральном методе. Если на входе системы действует сигнал вида, то на ее выходе формируется сигнал, являющийся сверткой входного сигналас импульсной временной характеристикой

(5.4)

Между исуществует однозначная связь, определяемая преобразованиями Фурье

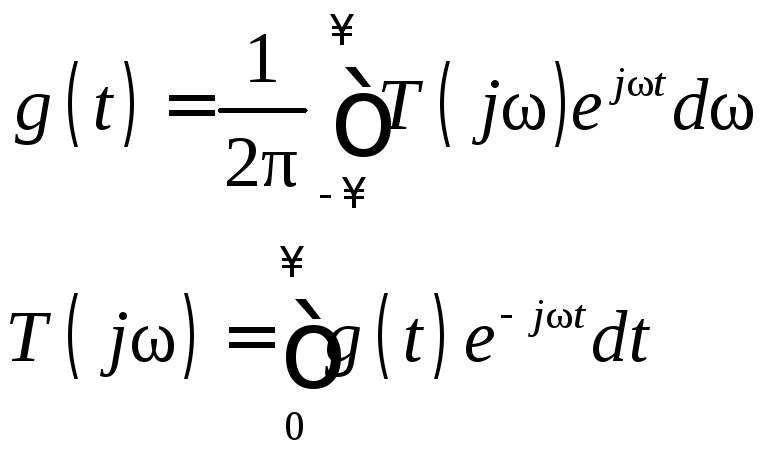(5.5)

б) Импульсная временная характеристика одиночного колебательного контура. Рассмотрим цепь, представленную на рис.5.2 и являющуюся параллельным колебательным контуром , на который действует входной сигнали к которому подключено некоторое (шунтирующее) сопротивление.

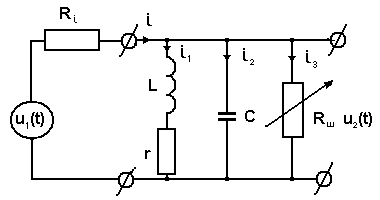
Рис.5.2.Параллельный колебательный контур с шунтирующим сопротивлением.

Источником сигнала служит генератор с внутренним сопротивлением. Запишем следующие уравнения, составленные в соответствии с законами Кирхгофа

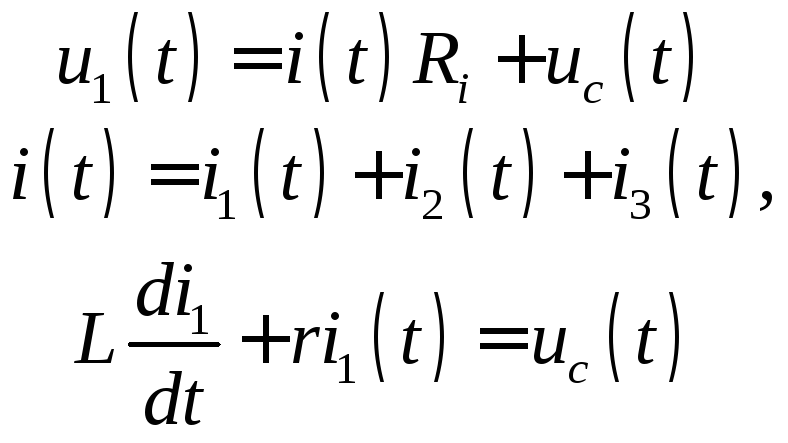(5.6) где и. Из уравнений (5.6) нетрудно получить дифференциальное уравнение, описывающее ток

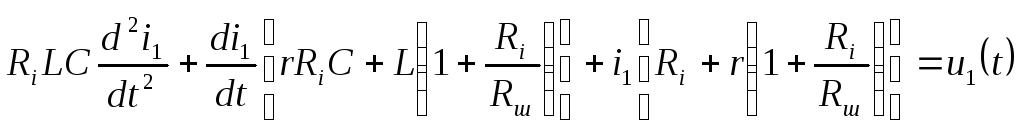(5.7)

Считая, что внутреннее сопротивление источника достаточно велико, получим

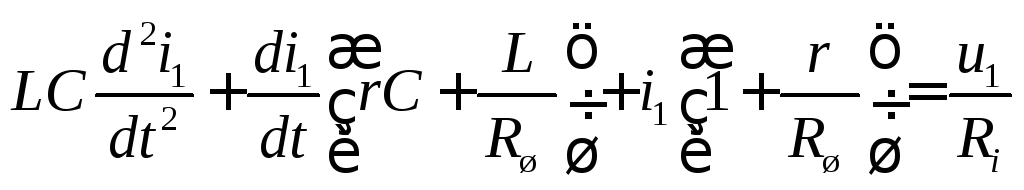(5.8) или с учетом замены и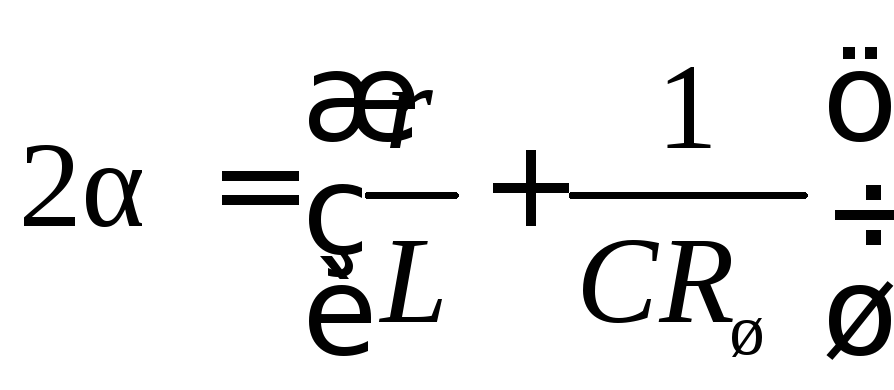

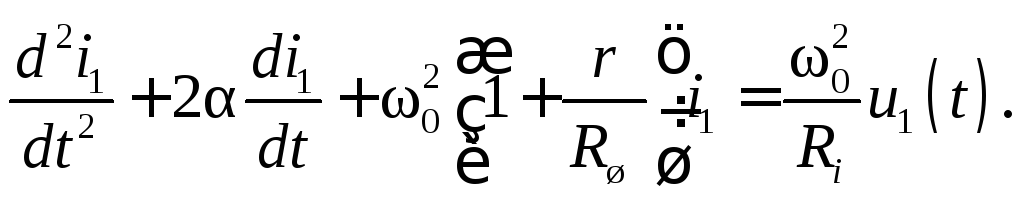(5.9) Для нахождения импульсной временной характеристики следует положить и применить преобразование Лапласа к уравнению (5.9) с нулевыми начальными условиями. Тогда

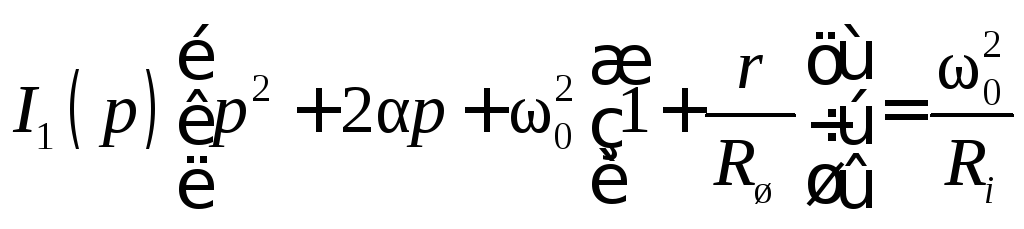(5.10) и

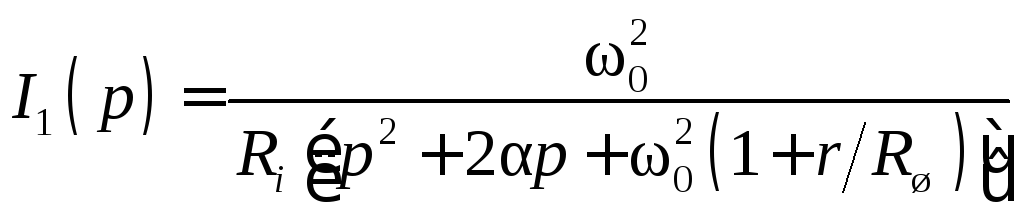(5.11) С другой стороны, из уравнения системы (5.6) имеем

(5.12)

и при условии , что индуктивное сопротивление катушки индуктивности существенно больше ее активного сопротивления,

(5.13) По изображению (5.13) можно найти оригинал, являющийся импульсной временной характеристикой контура .

В зависимости от соотношения между исуществуют три характерных типа решений: колебательный процесс, апериодический процесс и критический режим.

в) Колебательный процесс (рис.5.3) имеет место при условии .

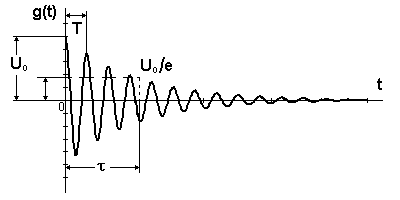
Рис.5.3. Затухающее колебание.

При этом

(5.14) где и- характеристическое сопротивление контура. Постоянную затухания можно записать как

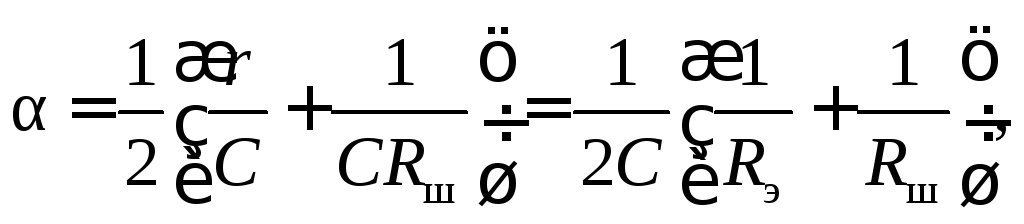(5.15) где - эквивалентное сопротивление контура. Нетрудно заметить, что подключение к контуру шунтирующего сопротивления, равного по величине эквивалентному сопротивлению, приводит к увеличению постоянной затуханияв 2 раза,что может быть использовано для экспериментального измерения .

г) Апериодический процесс наблюдается при значительных потерях, если .Функция, описывающая в этом случае импульсную временную характеристику, имеет вид

(5.16) где и- корни уравненияПоскольку оба корня вещественны, характеристикаявляется апериодической затухающей кривой.

д) Критический режим наблюдается при , и

(5.17) Он имеет место при переходе от колебательного процесса к апериодическому.

е) Импульсная временная характеристика системы связанных контуров.

В работе исследуется система, состоящая из двух параллельных колебательных контуров, связанных друг с другом через взаимную индуктивность (трансформаторная связь), схема которой представлена на рис. 5.4.

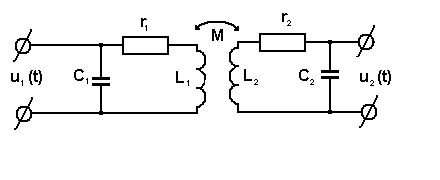
Рис.5.4. Система связанных колебательных контуров.

Поскольку характеристика является откликом системы на- функцию Дирака, для ее определения можно воспользоваться дифференциальными уравнениями, описывающими свободные колебания

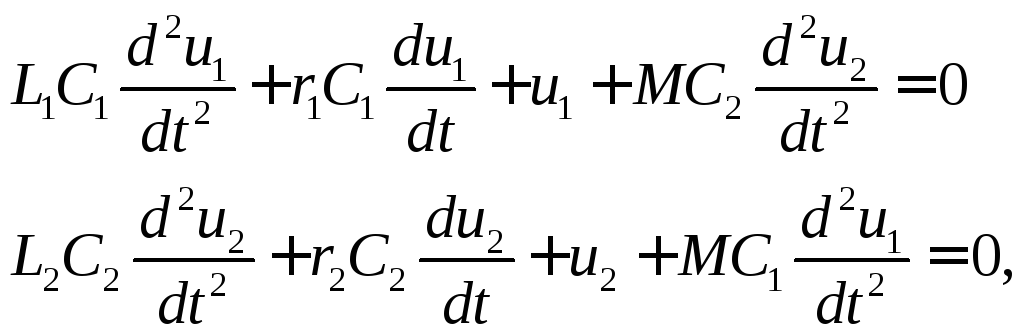(5.18) где и- напряжения на конденсаторахисоответственно.

Для упрощения задачи примем, что оба контура одинаковы, т.е. ,и. Положив в уравнениях (5.18),и введя коэффициент связи, получим

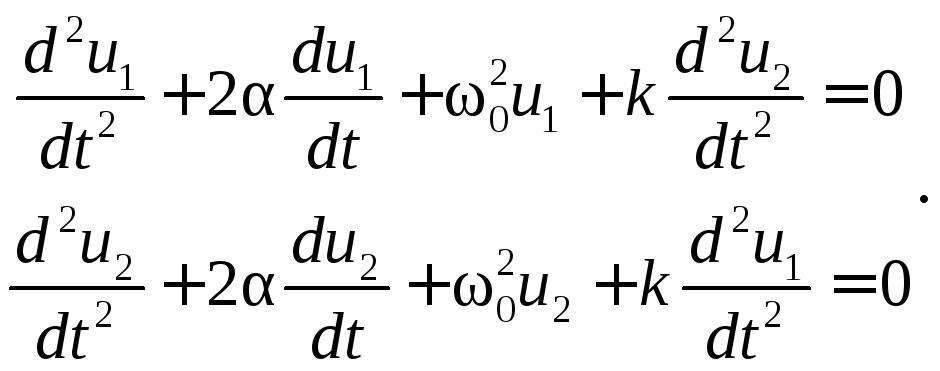(5.19) Решения этой системы уравнений, описывающие колебательные процессы, если добротность контуров достаточно высока, имеют вид

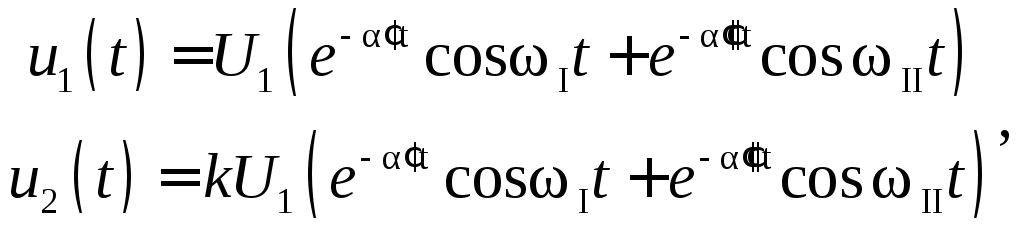(5.20) где - частоты связи, равные

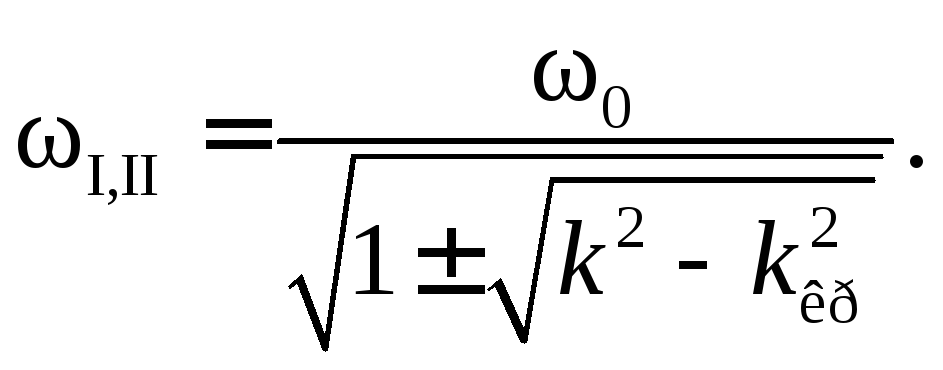(5.21) Они определяются коэффициентом связи и критическим коэффициентом связи, где- добротность контура системы.

Коэффициенты затухания иравны

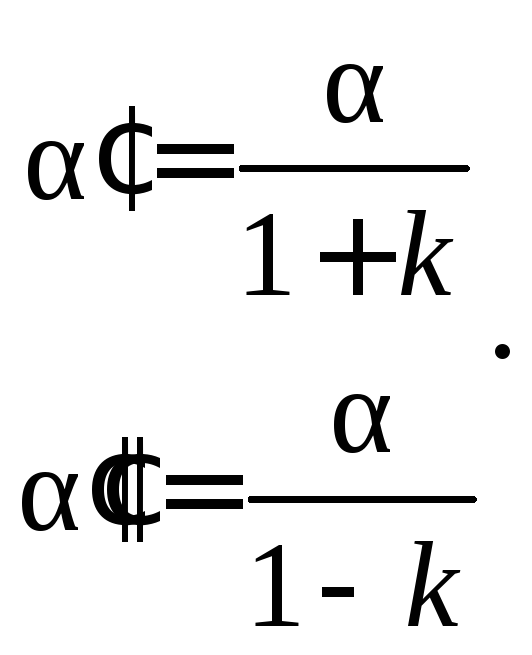(5.22) Если , то выражения (5.20) можно записать приближенно в виде

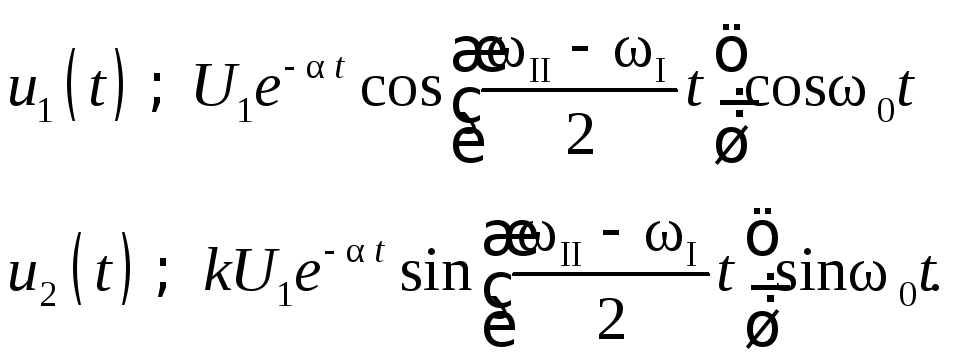(5.23)

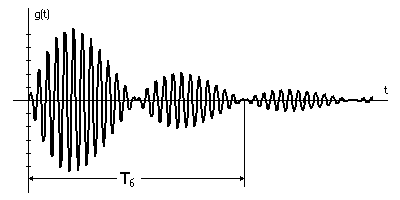
Рис.5.5. Биения при сильной связи.

Таким образом, даже при одинаковых частотах настройки отдельных контуров собственные колебания в системе характеризуются наличием биений двух колебаний с частотами (рис.5.5). Частота биений равна

(5.24) По измеренному периоду биений можно определить коэффициент связи двухконтурной системы.