§ 11.3. Иррациональные выражения
Этот класс интегралов является наиболее сложным, так как включает в себя множество подклассов интегралов, в каждом из которых свои приемы вычислений. Более того, кажущаяся очевидной замена переменной чаще всего не приводит к положительному результату.
Основная идея, реализуемая в этом классе интегралов, избавление от радикалов в подынтегральном выражении. Делается это, как правило, с помощью замены переменной. Но эта замена в большинстве случаев не очевидна. Поэтому для этих интегралов нужно особенно хорошо знать теорию.
1. Интегралы вида
,
где
по-прежнему дробно-рациональная функция
сложного аргумента. В этом случае
работает замена
,
где
наименьше общее кратное чисел
,
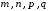другими словами,
наименьшее из чисел, делящихся нацело
на
.
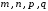Пример.
.
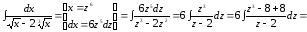
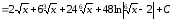2. Интегралы вида
.
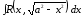Для этих интегралов имеются замены
переменных, напрямую приводящие их к
классу дробно-рациональных функций.
Однако предпочтительнее в этом случае
замена, переводящая интеграл в класс
тригонометрических функций. Это
,
тогда
.
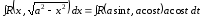Преобразование полученного в результате
замены переменной интеграла происходит
по правилам, установленным в классе
тригонометрических функций.
Пример.
.
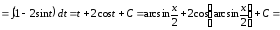
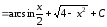3. Интегралы вида
.
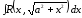Подынтегральная функция приводится к
рациональной относительно синуса и
косинуса функции заменой
,
откуда следует
.
Для преобразований полученного интеграла используем теорию, относящуюся к интегралам от тригонометрических функций.
Пример.
.
Если учесть формулы
,
,
то
,
.
Очевидно,
.
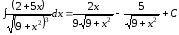4. Интегралы от
дифференциального бинома (биномиального
дифференциала)
.
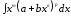Доказано, что в следующих трех случаях
интеграл сводится к дробно-рациональным
функциям.
А)
целое,
в этом случае интеграл является частным
случаем интегралов типа 1, и замена
,
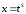где
наименьшее
общее кратное знаменателей дробей
и
,
приводит к интегрированию дробно-рациональной
функции.
В)
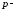дробное,
но
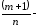целое. Тогда замена
,
где
знаменатель показателя степени
,
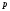сводит задачу к интегралу от
дробно-рациональной функции. Действительно,
.
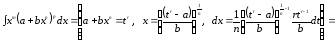
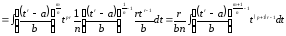Поскольку
целые по условию задачи, в подынтегральном
выражении присутствуют только целые
степени переменной
,
то есть после замены переменной получен
интеграл от дробно-рациональной функции.
С)
целое, тогда работает замена
,
где
знаменатель показателя степени
.
Итак,
,
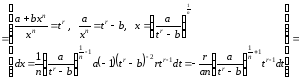
ясно, что при
целых все степени переменной
также целые.
Примеры.
1).
.
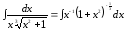Очевидно,
,
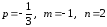следовательно, имеет место случай
,
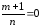тогда
.
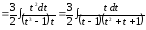Предложенная замена переменной, действительно, привела к дробно-рациональной функции. Разлагаем подынтегральную функцию на простые дроби
.
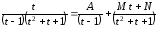После приведения дробей правой части равенства к общему знаменателю имеем
,
откуда следует система уравнений
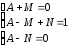
Из первого уравнения
имеем
,
из третьего
,
из второго
,
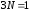тогда
, 
.
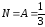Итак,
.
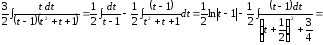
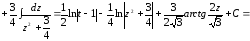
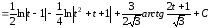Окончательно
.
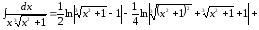
2).
.
Таким образом,
.
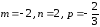Поскольку,
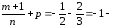целое,
необходима замена
:
.
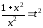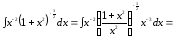
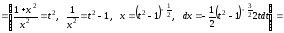
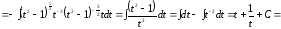
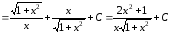Итак,
.
Примеры для самостоятельного решения
11.18.
,
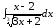11.20.
,
11.21.
,
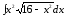11.22.
,
11.23.
,
11.24.
,
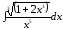11.25.
,
11.26.
,
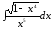11.27.
.
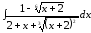Следует отметить, что интегралы четырех рассмотренных выше классов упрощаются с помощью замен переменных.
К ним следует добавить интегралы от некоторых сложных функций. Их преобразование производится с помощью замены аргумента (если она возможна), приводящего сложные функции к простым. Затем следует установить, класс, к которому принадлежит интеграл после указанного преобразования, и действовать в соответствии с этим.
Примеры.
1.
.
2.
.
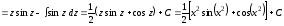Не следует забывать и об интегралах от произведений функций разного класса, для которых применима процедура интегрирования по частям.
Конечно, рассмотренные классы не исчерпывают всего многообразия существующих интегралов. Но именно они входят в программу курса высшей математики для естественных специальностей.
Заметим также, что
есть интегралы, точные решения которых
либо не существуют, либо они не могут
быть представлены в виде комбинации
элементарных функций, иногда такие
интегралы называют "не берущимися".
Например,
,
, 
, 
,
,
.
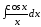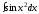Эти интегралы можно вычислить только приближенно.