Теорема существования и единственности решения дифференциального уравнения первого порядка

Пусть дано дифференциальное уравнение с начальным условием, причем функцияопределена в некоторой области, содержащей точку, и удовлетворяет в этой области условию Липшица по переменной:. Тогда на некотором отрезкесуществует единственное решение исходного уравнения, удовлетворяющее начальному условию.

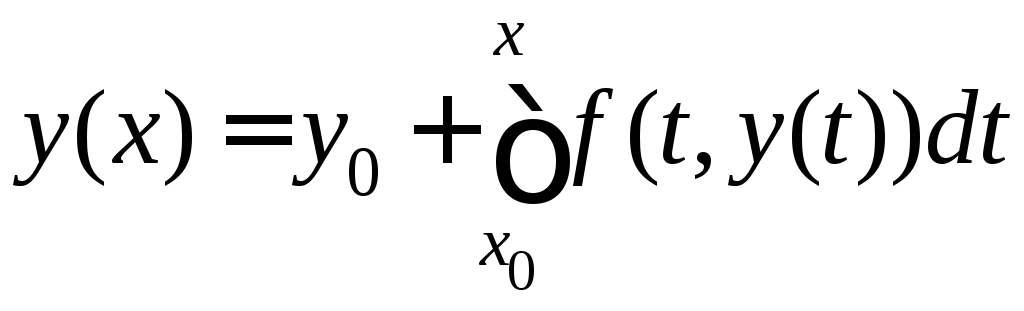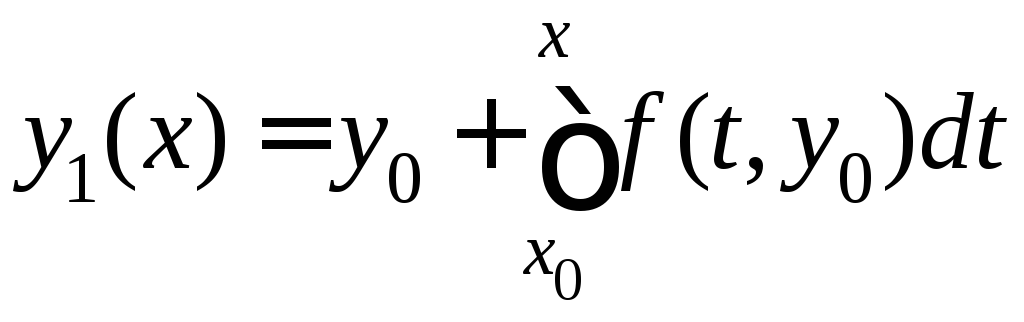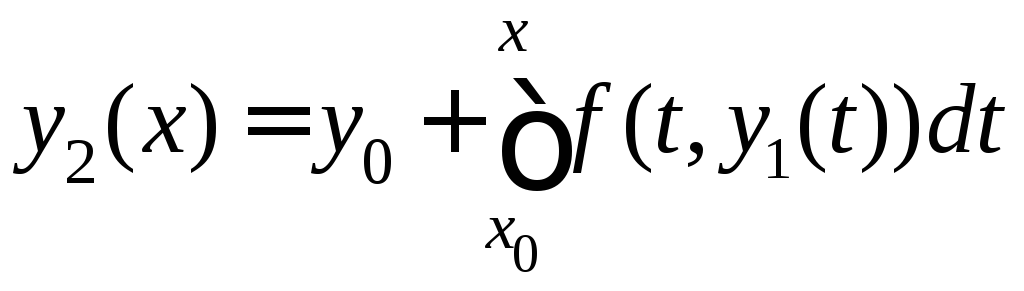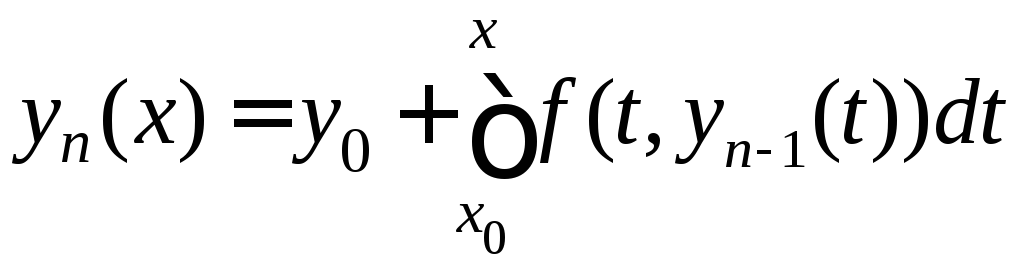Доказательство. Заданное дифференциальное уравнение с начальным условием равносильно интегральному уравнению . Предложим построить решение интегрального уравнения методом итераций: пусть,,…..,,…. Предложенный процесс итераций бесконечен. Покажем, что получаемая последовательность функций, сходится на некотором отрезке. Рассмотрим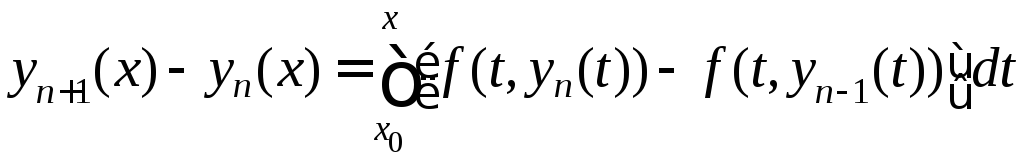. В соответствии с интегральными неравенствами и условием Липшица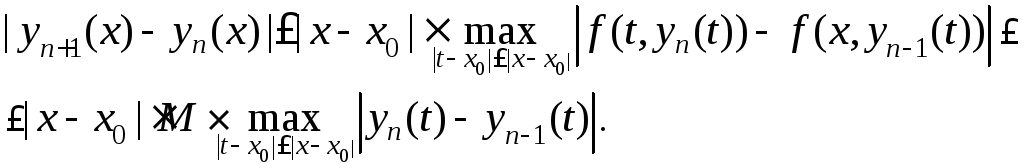

Выберем положительное число так, чтобы. Тогда

.

Пользуясь свойством модуля суммы, получим

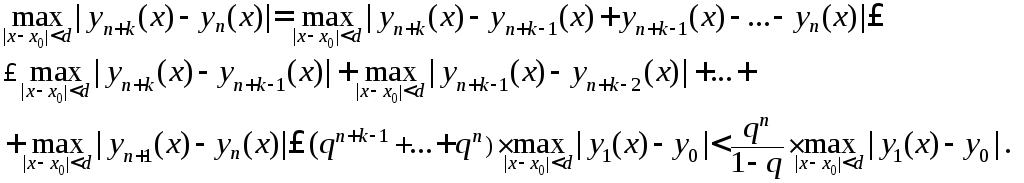
Вследствие того, что , значениеможно сделать сколь угодно малым при достаточно большом значении. Следовательно, при любом значениипоследовательность, фундаментальна, а значит, имеет предел. Следовательно, существует.

Единственность итерационного решения доказывается подобным способом: предположим, что существуют два решения исходного дифференциального уравнения (они же – решения приведенного интегрального уравнения) и. Следовательно,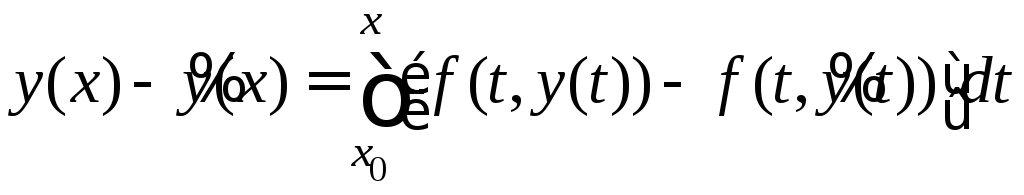. Отсюда согласно условию Липшица и выбору числаполучим. Последнее в силу того, что, возможно только в том случае, когда, что и доказывает единственность решения на выбранном отрезке.

Применение пакета программ maxima для решения дифференциального уравнения первого порядка и задачи Коши

Для решения дифференциальных уравнений и задач Коши удобно применять пакет математических программ MAXIMA.

Рассмотрим следующую задачу Коши. Найти решение дифференциального уравнения , удовлетворяющее условию.

Аналитическое решение. Представим производную в уравнении в виде отношения дифференциалов и разделим переменные: . Интегрируя обе части, получимили. Подставляя в полученное решение уравнения значенияи, получим. Поэтому решением поставленной задачи Коши является.

Решим задачу Коши, рассмотренную в предыдущем примере, с помощью компьютера. Для этого введем в память компьютера дифференциальное уравнение: (1+%e^x)*‘diff(y,x)=y*%e^x и нажмем Shift+Enter. На следующей строчке появится введенное уравнение. Заметим, что перед командой diff(y,x) обязательно должен стоять апостроф ‘, иначе компьютер продифференцирует y по x и выдаст 0.

Теперь для того, чтобы решить введенное дифференциальное уравнение (не выше второго порядка), посмотрим, под каким номером (например, (%o1)) запомнил компьютер введенное уравнение, этот номер стоит перед дифференциальным уравнением, выведенным компьютером на экран. Компьютер решит дифференциальное уравнение по команде ode2(%o1,y,x) и Shift+Enter и выведет на экран y=%c*(%e^x+1). Решение уравнения получено. Роль C в компьютерной записи выполняет %c. Теперь используем начальное условие. Для этого посмотрим номер, под которым компьютер вывел на экран решение уравнения (например, %o2). Введем команду ic1(%o2,x=0,y=2) и нажмем Shift+Enter. Мы получим решение задачи Коши y=%e^x+1.