7. Аналитическая геометрия на плоскости и в пространстве

Из названия раздела следует, что предметом исследования являются геометрические объекты, расположенные в некоторой плоскости. При этом исследования проводятся не с помощью построений, как это делалось ранее, а с использованием формул, определяющих эти объекты. Другими словами, применяется описанный выше координатный метод, увязывающий точку плоскости, как геометрический объект, с упорядоченной парой чисел, являющихся координатами этой точки в некоторой системе координат.

Ранее, в разделе "векторная алгебра" точке ставилась в соответствие упорядоченная тройка чисел, так как исследовались пространственные геометрические объекты.

Декартова и полярная система координат, связь между ними

Декартова прямоугольная система координат

В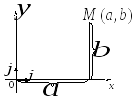ведем декартову прямоугольную систему координат как частный случай пространственной декартовой системы координат. В качестве базисных векторов выберем единичные векторыи, направленные вдоль осей, исоответственно.

Тогда началу координат соответствует пара чисел , точкаимеет координаты. При этом любой точке плоскости соответствует единственная пара чисел из области.

Рисунок 8.

Полярная система координат

Достаточно часто используется другая система координат – полярная. Вводится она следующим образом. Выберем некоторую точку плоскости и назовем ее полюсом, проведем через нее ось, называют ее полярной осью. Расстояние от полюса до некоторой точки обозначим, угол между полярной осью и лучом, соединяющим полюс с произвольной точкой плоскости – полярный угол – обозначим. Тогда паре чиселсоответствует точка плоскости.

Если считать , то в полярной системе координат каждой точке плоскости (кроме полюса!) соответствует

Рисунок 9.

единственная пара чисел - полярные координаты точки. За одним исключением - полюсу соответствует бесчисленное множество пар чисел , причемможет принимать любые значения в указанной выше области. Это является недостатком полярной системы координат, однако, польза от принятия данной координатной системы часто перекрывает указанный недостаток.

Пример. Паре чисел соответствует точка, лежащая на луче, проведенным под угломк полярной оси, причем расстояние от полюса до этой точки равно 2.

Связь между полярной и декартовой системами координат

Совместим две системы координат, как это показано на рисунке, то есть начало декартовой системы координат с полюсом, полярную ось – с осью. Тогда точкаимеет декартовы координаты, полярные ее координаты. Из рисунка следует, что, в то же время.

Рисунок 10.

С помощью этих формул в случае необходимости осуществляется переход от одной системы координат к другой. Так, точка с полярными координатами , имеет декартовы координаты,.

Расстояние между двумя точками плоскости

Пусть в декартовой системе координат точки заданы координатами и. Тогда вектор. Его длина и есть расстояние между этими точками. Очевидно

.

Деление отрезка в заданном отношении

Дан отрезок , причеми. Определить координаты

точки , делящей отрезок в отношении. Очевидно,.

Если векторы и сонаправлены (внутренняя точка отрезка), то последнее соотношение можно представить в векторной форме, и поскольку , получаем векторное уравнение

.

Известно, что два вектора равны, если равны их соответствующие проекции, отсюда следует

.

Из этой системы уравнений определяем искомые координаты точки :

.

Замечание 1. В полученных формулах существенно, какая точка отрезка считается первой, и какая второй. В самом деле, если , то. Другими словами, одна и та же точкаделит отрезкиив различном отношении.

Замечание 2. Если за основное принять векторное равенство , точкаможет находиться вне отрезка, тогда векторыи противоположно направлены, полученные формулы при этом справедливы, но.

При имеем известные их школы формулы координат середины отрезка

.