МОДЕЛИРОВАНИЕ ХИМИКО-ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ КАК ОБЪЕКТОВ УПРАВЛЕНИЯ УЧЕБНО-ИССЛЕДОВАТЕЛЬСКИЙ ПРАКТИКУМ

Контрольные вопросы

1.Частные уравнения интенсивности источников (стоков) тепла

впотоках: теплообмен.

2.ММ проточного аппарата идеального смешения с учетом источников тепла.

3.ММ проточного аппарата идеального вытеснения с учетом источников тепла.

4.ММ теплообменника типа смешение – смешение.

5.ММ теплообменника типа вытеснение – смешение.

6.ММ теплообменника типа вытеснение – вытеснение.

21

3. МОДЕЛИРОВАНИЕ КАТАЛИТИЧЕСКОГО РЕАКТОРА КОЖУХОТРУБЧАТОГО ТИПА

Цель работы: изучение особенностей моделирования каталитических химических процессов, сопровождающихся выделением или поглощением тепла, на примере реактора кожухотрубчатого типа с катализатором, помещенным в трубное пространство.

Теоретические сведения

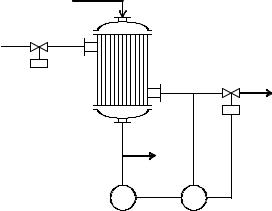
Многие процессы химической технологии осуществляются в аппаратах кожухотрубчатого типа. В таких аппаратах чаще всего проводят химические реакции, характеризирующиеся необходимостью подвода тепла извне, либо охлаждения (экзо- и эндотермические реакции). При этом процессы могут идти в присутствии катализатора либо в газофазном потоке. Общая схема такого аппарата представлена на рис. 3.1.

T 0, CA0

Tx0

Рис. 3.1. Каталитический реактор кожухотрубчатого типа

В качестве моделируемого процесса в работе рассмотрен процесс риформинга, который в схематичном виде можно представить следующим образом:

22

А → продукты реакции + Q.

Реакция сопровождается выделением тепла, следовательно, для поддержания требуемого температурного режима необходим постоянный отвод тепла. Однако переохлаждение реакционного пространства недопустимо, так как в этом случае реакция затухает.

Для составления математического описания реактора приняты следующие допущения:

1)трубное пространство аппарата следует модели реактора идеального вытеснения;

2)в кожухотрубном пространстве температура постоянна. Скорость химической реакции представляет собой функцию

состава реакционной массы, температуры, давления и других факторов.

Пусть выражение для скорости реакции имеет вид

где CA – концентрация исходного компонента, кмольм3 ; K – константа скорости реакции, 1мин;

T – температура смеси, К;

R – универсальная газовая постоянная, Джкмоль К; E – энергия активации, Джкмоль; ;

K0i – предэкспоненциальный множитель, 1мин.

Дифференциальное уравнение, описывающее изменение концентрации компонента А, имеет следующий вид:

где F – площадь теплообмена, м2 ;

t– астрономическое время;

υ– объемный расход реакционной массы, м3мин;

qA – интенсивность расходования исходного вещества, кмольм3 мин.

23

Как упоминалось выше, рассматриваемая реакция является экзотермической (идет с выделением тепла), поэтому в математическом описании необходимо учесть тепловой эффект реакции и теплообмен реагирующего в трубном пространстве потока со средой, находящейся в межтрубном пространстве.

Уравнение теплового баланса имеет вид

24

Применительно к кожухотрубчатому каталитическому реактору изменение температуры и концентрации исходного реагента нагляднее изучать не по длине аппарата, а по времени пребывания элементов потока в аппарате (реакционной зоне):

где τ – среднее время пребывания вещества в аппарате.

Выразим текущее время пребывания как функцию конструктивных характеристик аппарата и расхода потока:

где τ – время пребывания вещества в аппарате.

25

Для упрощения системы (3.10) все постоянные коэффициенты можно сгруппировать и переобозначить:

С учетом (3.11) система (3.10) приобретает окончательный вид

Система (3.12) решается любым из известных методов численного или аналитического решения систем дифференциальных урав-

нений при наличии начальных условий (CA (0) = CA0 ; T (0) = T 0 )

с использованием данных о конструктивных характеристиках аппарата, физических свойствах смеси, тепловом эффекте реакции.

Задание и порядок выполнения работы

1.Ознакомиться с основными теоретическими сведениями.

2.В соответствии с вариантом задания (табл. 3.1) составить систему дифференциальных уравнений вида (3.12).

3.Используя один из методов решения систем дифференциальных уравнений программы Pr&Co&Rk.exe, пакетов Matlab или

MathCad, получить кривые состояния реактора по температуре

иконцентрации исходного вещества.

4.Для заданной температуры и концентрации реагентов на входе подобрать температуру хладагента, при которой температура по длине реактора не превышает заданного значения Тогр.

5.Сделать выводы по работе.

26

Содержание отчета

1.Теоретические сведения.

2.Система математического описания процесса.

3.Исходные данные и результат работы (найденное значе-

ние Тх).

27

Окончание табл. 3.1

Контрольные вопросы

1.ММ проточного аппарата идеального вытеснения с учетом источников вещества и тепла.

2.Частные уравнения интенсивности источников (стоков) вещества и тепла в потоках: химические реакции и теплообмен.

28

4. МОДЕЛИРОВАНИЕ СИСТЕМЫ УПРАВЛЕНИЯ ХИМИЧЕСКИМ РЕАКТОРОМ

Цели работы: получение практических навыков математического моделирования процессов, происходящих в химическом реакторе; получение с помощью вычислительного эксперимента на модели настроек регулятора; моделирование системы управления реактором. Задание на выполнение работы может служить темой курсовой работы студентов по дисциплине «Моделирование систем».

Исходной базой для проектирования любой системы управления являются математические модели типовых технологических процессов. Построение математической модели всегда начинается с составления формализованного описания процессов, происходящих в объекте моделирования. Основными процессами, протекающими в химическом реакторе, являются химические превращения, сопровождающиеся выделением или поглощением тепла (экзотермические и эндотермические реакции). Как правило, наиболее часто встречаются реакции следующих типов:

•линейные, когда происходит последовательное превращение одного вещества в другое: А→ В→ С→ D (например, реакции полимеризации);

•обратимые, когда происходит одновременное протекание как прямого, так и обратного превращения: A B (большинство химических реакций, например окисление сернистого ангидрида в производстве серной кислоты);

•реакции синтеза, когда из двух или более реагентов образуется один целевой продукт реакции: А→ В← С (например, получение нитроглицерина);

•реакции разложения, когда из одного вещества образуются два или более продукта: А← В→ С (например, процесс кальцинации).

На практике в чистом виде такие реакции, как правило, не встречаются. В промышленных химических процессах обычно протекают реакции смешанных типов, например:

29

В C

Скорость химической реакции представляет собой функцию состава реакционной массы, температуры, давления и других факторов. В частности, для реакций на приведенных схемах выражение для скоростей можно представить в виде

1 2

A P S

3

C

выражения для скоростей простых реакций, предполагая для них первый порядок, можно представить в следующем виде:

30