Технические измерения и приборы

В качестве нормирующего значения используется верхний предел измерения, диапазон измерения или, для двухсторонних шкал, арифметическая сумма верхнего и нижнего пределов измерения,

Форма представления погрешности измерительных преобразователей

У измерительных преобразователей результаты измерений представляются в единицах выходной величины преобразователя. В связи с этим для измерительных преобразователей принято различать погрешности по входу и выходу.

При определении этих погрешностей необходимо знать приписанную данному измерительному преобразователю функцию преобразования или градуировочную характеристику Y = f (X).

Номинальная или идеальная функция преобразования –

функция преобразования, которая приписана измерительному устройству данного типа, указана в его паспорте и используется при выполнении измерений.

Реальная функция преобразования – функция преобразования,

которой обладает конкретный экземпляр измерительного устройства. Несовершенство конструкции и технологии изготовления при-

водит к различию реальной и номинальной функции преобразования. Это отличие определяет погрешность данного измерительного устройства.

Абсолютная погрешность измерительного преобразователя по выходу ( Y) – разность между действительным значением величины на выходе преобразователя (Yп) и значением величины на выходе (Yд), которое определяется по действительному значению величины на входе с помощью градуировочной характеристики, приписанной преобразователю,

где Yп – фактическое значение выходного сигнала преобразователя; Yд – значение выходного сигнала, который должен вырабатываться

51

преобразователем, лишенным погрешности, при том же значении входного сигнала. Значение Yп определяют с помощью образцового средства измерений, а значение Yд рассчитывают с помощью функции преобразования по действительному значению входной величины Xд, которое воспроизводится мерой или определяется с помощью образцового средства измерений,

Из (2.24) и (2.25) находим

Абсолютная погрешность измерительного преобразователя по входу ( X) – разность между значением величины на входе преобразователя (Xп), определяемым по действительному значению величины на его выходе (Yд) с помощью градуировочной характеристики, приписанной преобразователю, и действительным значением величины на входе преобразователя (Xд),

Значение Xд определяется с помощью образцового средства измерений или воспроизводится мерой, а значение Xп определяется по значению Yп выходного сигнала с помощью функции преобразования, решенной относительно X, т.е. Xп = (Yп), где – функция обратного преобразования. Таким образом,

Относительная погрешность измерительного преобразова-

теля по входу ( X) – отношение абсолютной погрешности измерительного преобразователя по входу к действительному значению величины на входе,

52

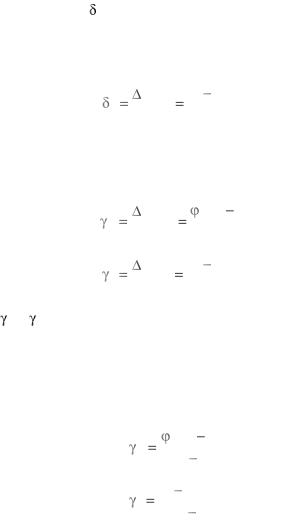
Относительная погрешность измерительного преобразова-

теля по выходу ( Y) – отношение абсолютной погрешности измерительного преобразователя по выходу к значению величины на выходе, определяемому по действительному значению величины на входе по градуировочной характеристике,

Приведенная погрешность измерительного преобразователя по входу (выходу) – отношение абсолютной погрешности к нормирующему значению входного XN (выходного YN) сигнала,

где X и Y – приведенная погрешность измерительного преобразователя по входу и выходу соответственно.

Обычно в качестве нормирующего значения используется

Для измерительных преобразователей с линейной функцией преобразования вида Y – Yн = K (X – Xн) приведенные погрешности по входу и выходу в соответствии с (2.33) и (2.34) определяются выражениями

53

где K – коэффициент преобразования измерительного преобразователя, определяемый отношением (Yв – Yн) / (Xв – Xн).

5. При применении измерительных устройств и оценки погрешности измерений важным являются сведения о зависимости по-

грешности от значения измеряемой величины в пределах диапа-

зона измерений.

Зависимость погрешности от значения измеряемой величины определяется конструкцией и технологией изготовления измерительного устройства Зависимость погрешности от значения измеряемой величины свойственна всем измерительным устройствам одной конструкции. Влияние технологии изготовления на рассматриваемую зависимость индивидуально для каждого экземпляра.

Для определения зависимости погрешности измерительных устройств от значения измеряемой величины используют понятие номинальной и реальной функций преобразования измерительного устройства.

Отклонения реальной характеристики от номинальной зависят от значения измеряемой величины. По этому признаку погрешности принято разделять на аддитивную, мультипликативную, линейности и гистерезиса.

Аддитивная погрешность или погрешность нуля измери-

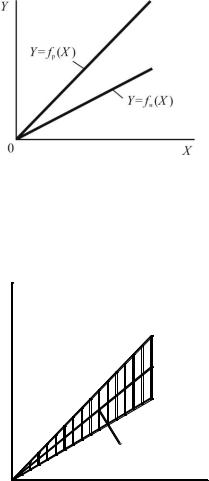
тельных устройств – погрешность, которая остается постоянной при всех значениях измеряемой величины (рис. 2.16).

На рис. 2.16 видно, что реальная функция преобразования Y = fР (X) смещена относительно номинальной Y = fн (X), поэтому выходной сигнал измерительного устройства при всех значениях измеряемой величины X будет больше на одну и ту же величину, чем должен быть, в соответствии с номинальной функцией преобразования.

54

но возрастает (или убывает) с увеличением измеряемой величины

(рис. 2.18).

Графически появление мультипликативной погрешности интерпретируется поворотом реальной функции преобразования относительно номинальной (см. рис. 2.18).

Рис. 2.18. Систематическая мультипликативная погрешность

Если мультипликативная погрешность является случайной, то реальная функция преобразования представляется областью, показанной на рис. 2.19.

Y

Y =f н (X )

Рис. 2.19. Случайная мультипликативная погрешность

56

Причина возникновения мультипликативной погрешности – изменение коэффициентов преобразования отдельных элементов и узлов измерительных устройств.

На рис. 2.20 показано взаимное расположение номинальной и реальной функций преобразования измерительного устройства в случае, когда отличие этих функций вызвано нелинейными эффектами.

Если номинальная функция преобразования линейная, то вызванную таким расположением реальной функции преобразования систематическую погрешность называют погрешностью линейности. Причинами данной погрешности могут быть конструкция измерительного устройства и нелинейные искажения функции преобразования, связанные с несовершенством технологии производства.

Погрешность гистерезиса наиболее существенная и трудноустранимая систематическая погрешность измерительных устройств (от греч. hysteresis – запаздывание) или погрешность обратного хода, выражающаяся в несовпадении реальной функции преобразования измерительного устройства при увеличении (прямой ход) и уменьшении (обратный ход) измеряемой величины. Графически погрешность, вызванная эффектом гистерезиса, представлена на рис. 2.21.

57

Y

Y =f р (X )

Y =f н(X )

Рис. 2.21. Погрешность гистерезиса

Причинами гистерезиса являются: люфт и сухое трение в механических элементах, гистерезисный эффект в ферромагнитных материалах, внутреннее трение в материалах пружин, явление упругого последействия в упругих чувствительных элементах, явление поляризации в электрических, пьезоэлектрических и электрохимических элементах.

Существенным при этом является тот факт, что форма получаемой петли реальной функции преобразования зависит от предыстории, а именно от значения измеряемой величины, при котором после постепенного увеличения последней начинается ее уменьшение (на рис. 2.21 это показано пунктирными линиями).

2.6. НОРМИРОВАНИЕ МЕТРОЛОГИЧЕСКИХ

ХАРАКТЕРИСТИК СРЕДСТВ ИЗМЕРЕНИЙ

Средства измерений допускаются к применению только в том случае, если нормированы их метрологические характеристики, т.е. установлены нормы. Сведения о них приводятся в технической документации на средства измерений.

Нормирование метрологических характеристик обеспечивает взаимозаменяемость средств измерений и единство измерений в госу-

58

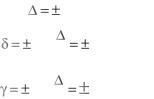
дарственном масштабе. Реальные значения метрологических характеристик средств измерений определяются при их изготовлении, а затем периодически проверяются в процессе эксплуатации. При наличии отклонений хотя бы одной нормированной метрологической характеристики от нормы средство измерений регулируется, подвергается ремонту или бракуется и изымается из обращения.

2.6.1. Нормирование метрологических характеристик измерительных устройств

Нормирование характеристик, определяющих точность измерений, выполняемых с помощью данного средства измерения (основная и дополнительная погрешности, размах, вариация), имеет определенную специфику

Основная погрешность устройства для технических измерений нормируется путем установления предела допускаемой абсолютной, относительной или приведенной погрешности,

где X – входной сигнал измерительного устройства, XN – нормирующее значение.

Способ задания пределов допускаемой основной погрешности для измерительных приборов и преобразователей определяется зависимостью их погрешности от значения измеряемой величины и требованиями простоты. Если у измерительных устройств данного типоразмера после регулировки погрешность практически не зависит от значения измеряемой величины, т.е. является аддитивной, то предел допускаемой основной погрешности нормируется абсолютной погрешностью, определяемой по формуле (2.37), либо приведенной погрешностью, определяемой по формуле (2.39).

59

Если погрешность измерительных устройств данного типоразмера является мультипликативной и пропорциональна значению измеряемой величины, т.е.

то предел допускаемой основной погрешности удобно нормировать через относительную погрешность, определяемую по формуле (2.38), так как норма определяется одним числом,

Значение предела относительной или приведенной погрешности определяется из ряда предпочтительных чисел [1; 1,5 (1,6); 2; 2,5 (3); 4; 5; 6]∙10n, где n = +1, 0, –1, –2, … Числа 1,6 и 3 допускаются к применению, но не рекомендуются.

Дополнительная погрешность нормируется в тех случаях, ко-

гда при изменении влияющих величин в рабочей области основная погрешность превышает установленный для нее предел. Дополнительная погрешность нормируется:

1)в виде постоянного значения доп для всей рабочей области влияющей величины или по отдельным интервалам этой области;

2)путем указания отношения предела допускаемой дополнительной погрешности, принятой для регламентируемого интервала влияю-

щей величины, к значению этого интервала, т.е. доп/ ( – регламентируемый интервал влияющей величины );

3) путем указания зависимости предела допускаемой дополнительной погрешности от влияющей величины, т.е. доп = ).

Измерительные устройства принято разделять на классы точности. Класс точности ( ) – обобщенная характеристика средств измерений, которая определяется пределами допускаемых основной и дополнительной погрешностей.

60