Омский государственный технический университет

Кафедра «Автоматизированные системы обработки информации и управления»

Отчет

по лабораторной работе №2

«Исследование процессов кодирования и декодирования при передаче дискретных сообщений кодами Хэмминга»

Выполнил:

студент гр. Ас-330

Юдин Е.Б.

Проверил:

Юдин Е.Б.

Омск-2002

Задание к лабораторной работе:

1. Определить длину информационной i , длину проверочной k последовательности кода и формируем код Хэмминга.

2. Построить порождающую матрицу кода. 3. Построить проверочные матрицы кода в модифицированном (с проверкой на четность) виде. 4. Сформировать системы проверочных и синдромных уравнений. 5. Сформировать кодовое слово исследуемого кода, ввести одиночную ошибку и показать ее исправление путем вычисления синдрома. 6. Показать на примере, что код не гарантирует обнаружение тройных ошибок.

7. Произвести первичное декодирование принятого сообщения, закодированного кодом Хэмминга. При этом осуществить обнаружение и исправление ошибок в кодовых словах, используя методику исправления с вычислением синдрома.

Результаты выполнения работы

1. Определяем длину информационного i и длину проверочного к последовательного кода и формируем код Хэмминга.

Нам дана длина кода – n. Информационные и проверочные биты определим из соотношения:

2^к > i+k (1)

Т.к. длина кода n=7, а длину информационного кода возьмем равную i=4, то согласно соотношению (1) количество проверочных бит k=n-i, k=3:

2³ > 4+3.

Код (7,4,3).

Формируем код Хэмминга: k₁ k₂ i₃ k₄ i₅ i₆ i₇ (проверочные биты стоят на местах: 2⁰, 2¹, 2², 2³ и т.д.):

1. 00001

2. 00010

3. 00011 00001 k_{1 =} i₃ i₅ i₇

4. 00100 00010  k₂ = i₃ i₆ i₇

5. 00101 00100 k₄ = i₅ i₆ i₇

6. 00110

7. 00111

2. Кодом Хэмминга называется (n,k)-код, проверочная матрица которого имеет i = n-k строк и 2ⁱ-1 столбцов, причем столбцами являются все различные ненулевые последовательности. Столбец Р – проверка на четность. Строим порождающую матрицу кода, которая состоит из единичной матрицы I_i, содержащей информационные биты и прямоугольной матрицы K_i,k, составленной из проверочных битов:

G =

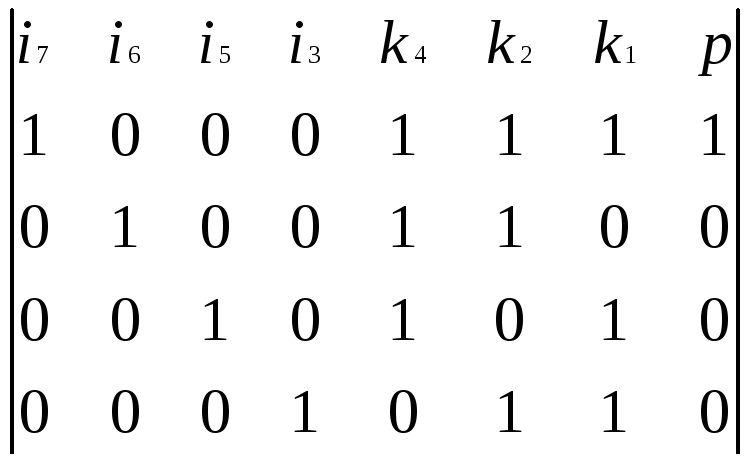
3. Построим проверочную матрицу.

Проверочная матрица имеет вид H_(n,i)=|K_i,k^T, I_i|; где I_i - единичная матрица;

K_i,k^T - прямоугольная матрица в транспонированном виде матрицы K_i,k из порождающей матрицы. Проверочная матрица любого кода Хэмминга всегда содержит минимум три линейно зависимых столбца.

В нашем случае H_(8,4)=|K_4,4^T, I₄|: K_4,4^T =

Отсюда получаем проверочную матрицу вида:

H =

4. Сформируем системы проверочных и синдромных уравнений. Для этого умножим единичную матрицу I_8,8 на транспонированную проверочную матрицу H_8,4,получим:

 =

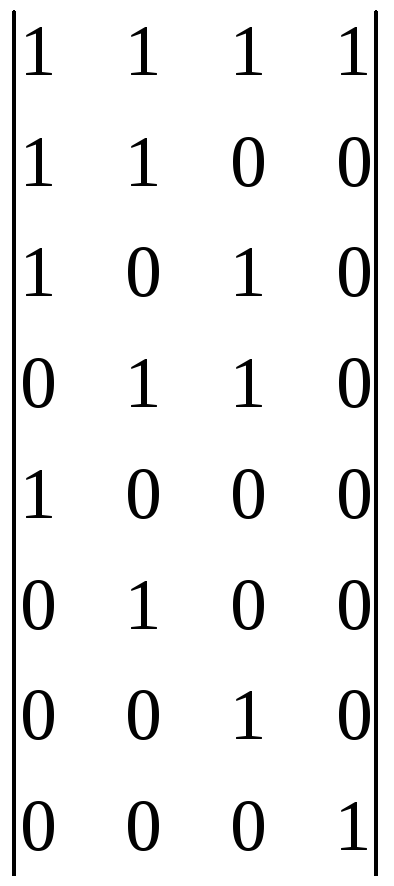5. Сформируем кодовое слово исследуемого кода, введем одиночную ошибку и покажем ее исправление путем вычисления синдрома. Произведение любого кодового слова G₁ на транспонированную проверочную матрицу дает нулевой вектор размерности (n-i): G_i·H_n,i^T =[00...]

Возьмем любой код из порождающей матрицы G, умножим на H^T и проверим на наличие ошибки:

 =

Как видно из полученного результата - ошибки нет.

Произведение некоторого кодового слова G_i', т.е. с ошибкой, на транспонированную проверочную матрицу называется синдромом и обозначается S_i: G_i'·H_{(n, k)}^T= S_i.

Пусть переданное кодовое слово G=00101010, а принятое слово - G'=00100010. Синдром, соответствующий принятому слову будет равен S=G'·H_(8,4)^T=[1000]. Вычисленный синдром указывает на ошибку в пятой позиции. Покажем это:

 = 1000

6. Код Хэмминга позволяет выявить только одну ошибку.

Показать на примере, что код не гарантирует обнаружение тройных ошибок.

Пусть передано кодовое слово 10001111. Сделаем три ошибки и получим код 10100101. Проверим его:

 = 0000

Как видно из полученного результата, проверяемый код не содержит ошибок, хотя на самом деле в нем три ошибки.

7. Произвести первичное декодирование принятого сообщения, закодированного кодом Хэмминга. При этом осуществить обнаружение и исправление ошибок в кодовых словах, используя методику исправления с вычислением синдрома. Возьмем произвольный информационный код: i = 0110.

Вычислим для него проверочные биты. Для этого из порождающей матрицы берем прямоугольную матрицу, состоящую из проверочных битов, и находим k:

K_i,k =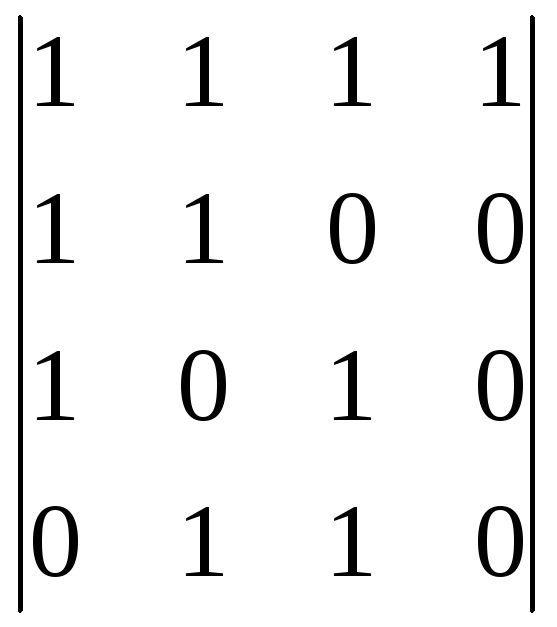  k = 0110

Полученный код имеет вид:

Декодирование означает исключение проверочных битов. Получим код 0110.

Проверим наш код на наличие ошибок:

 = 0000

Вычисленный синдром показывает на то, что код ошибки не содержит.

Введем ошибку и проверим ее при помощи матрицы синдромных уравнений:

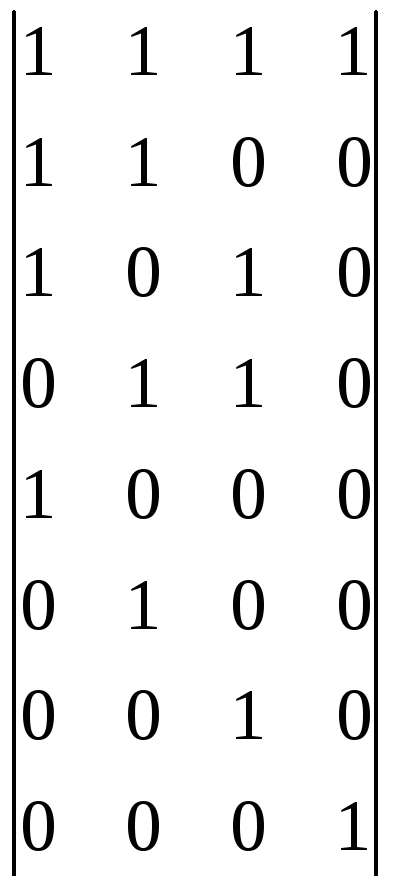 = 1010

Вычисленный синдром указывает на ошибку в третьей позиции.

0