САОД-2

Курсовая, экзамен. Ахо, кроме Паркинсона и теории сложности.

1. Алгоритмы на графах

2. Алгоритмы на деревьях

3. Методы разработки ПО

4. Теория сложности

1. Алгоритмы на графах

   1. Графы

В ориентированном графе каждая дуга представлена упорядоченной парой вершин.

Произвольный граф будем обозначать где V – множество вершин, E – множество дуг.

Путём называется последовательность вершин 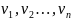, таких, что существуют дуги .

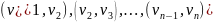Длиной пути для невзвешенного (неразмеченного) графа называется количество дуг.

Каждому узлу, кроме имени, может быть задана метка (значение), хранящееся в узле. Тогда граф размечен (или взвешен) по узлам.

Дуга может содержать также метку (вес, значение, цену). Тогда граф размечен (взвешен) по дугам.

Длина пути на взвешенном графе равна сумме длин дуг.

В графах используется неевклидовое расстояние.

2. Представление графов

1. Матрица смежности

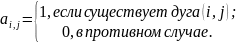
	1	2	3	4
1	0	1	1	1
2	1	1	0	1
3	0	0	0	0
4	1	0	0	0

Недостаток один – в разреженных матрицах для слабосвязанного графа много нулей, т.е. неэкономное использование памяти.

Одно большое достоинство – матрица смежности позволяет операции над графами сводить к операциями над матрицами.

2. Матрица инцидентности

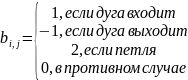
	(1,2)	(2,1)	(1,4)	(4,1)	(2,2)	(2,4)	(1,3)
1	-1	1	-1	1	0	0	-1
2	1	-1	0	0	2	-1	0
3	0	0	0	0	0	0	1
4	0	0	1	-1	0	1	0

Недостатков куча.

Достоинство – легко составить уравнение баланса для одного узла.

3. Список смежности

3. Элементы ЛСС – существующие дуги, исходящие из головы.

4. Список дуг

В любом виде – ЛСС или массив.

4. Задача нахождения кратчайшего расстояния. Алгоритм Дейкстры

Пусть дан орграф , у которого все дуги имеют неотрицательные веса. Задача состоит в нахождении кратчайшего расстояния от одной заданной вершины, называемой источником, до всех остальных вершин. Заметим, что если требуется найти кратчайшее расстояние между конкретной парой вершин, то эта задача имеет тот же порядок сложности, что и общая (просто может иметь досрочное завершение внешнего цикла), если конечная вершина помещена в множество S.

Задача нахождения кратчайшего расстояния с одним источником решается алгоритмом Дейкстры (Dijkstra).

Суть алгоритма в следующем: алгоритм строит множество S вершин, до которых кратчайшее расстояние найдено. На каждом шаге в множество S добавляется очередная вершина графа , до которой самое короткое расстояние от источника на данный момент. Эти расстояния хранятся в массиве D размерностью , где - число вершин.

Выбирается узел w, после чего пересчитывается расстояние от источника до смежных с w узлов из множества .

Если маршрут через w короче существующего, новая длина пути запоминается в массиве D. Эта проверка выполняется для каждого узла из .

Алгоритм завершается, когда или .

Пример алгоритма из Ахо.

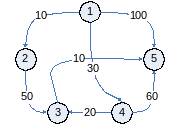
Матрица цен для этого графа:

С	1	2	3	4	5
1	∞	10	∞	30	100
2	∞	∞	50	∞	∞
3	∞	∞	∞	∞	10
4	∞	∞	20	∞	60
5	∞	∞	∞	∞	∞

Важное примечание – нули в матрице цен ставить нельзя, потому что это будет означать, что путь из одного в другой минимален. Чтобы не допустить такой коллизии, нужно ставит ∞, и это позволит не выбрать этот путь.

Массив P[i]=j означает, что в узел i мы пришли из узла j, что обеспечило длину D[i].

Инициализация

Ввод w //Ввод источника

S≔w //то есть источник

For v≔1 to |V| do

Begin

D[v]≔C[w,v]; //инициализации начальных расстояний

//берётся из матрицы цен

P[v]≔w;

End;

Основной цикл

While (V\S≠∅) do

Begin

W≔i, i удовл. условию ;

/*Выбор из множества V\S такой вершины w,

что значение D[w] минимально*/

S≔S+{w};

For v V\S do //for v≔1 to n do if not V in S then

If D[v]>D[w]+C[w,v] then

Begin

D[v]≔D[w]+C[w,v];

P[v]≔w;

End;

End;

End.

шаг	w	S	D[2]	D[3]	D[4]	D[5]	P[1]	P[2]	P[3]	P[4]	P[5]
иниц	1	{1}	10	∞	30	100	1	1	1	1	1
1	2	{1,2}		60					2
2	4	{1,2,4}		50		90			4		4
3	3	{1,2,4,3}				60					3
4	5	{1,2,4,3,5}

Procedure Vyvod;

Begin

Dijkstra;

For v≔1 to |v| do

Begin

ВЫВОД Путь длиной D[v] состоит из вершин:

Path();

End;

End;

Домашняя работа. Построить процедуру Path.