1.6 Методические указания для работы студентов на практическом занятии

• Преподаватель проверяет уровень подготовки студентов к практи­ческому занятию.

• Под руководством преподавателя студенты разбирают вопросы, вынесенные на самостоятельную подготовку.

• Студенты самостоятельно выполняют предложенные преподавателем индивидуальные задания по расчету вероятностных характеристик сообщения.

• Преподаватель подводит итоги занятия.

1.7 Индивидуальные задания

Считая частоту появления символов постоянной и определяемой указанным текстом, определить вероятностные характеристики сообщений и рассчитать количество информации, связанное с каждым символом в сообщении, связанное в среднем с одним символом и в сообщении в целом. (Длина текста не превышает 30 символов, желательно чтобы текст содержал повторяющиеся символы). Примеры текста.

1. Черти чертили чертеж

2. Шла Саша по шоссе

3. Узоры как розы

4. На дворе трава, на траве дрова

5. Захар – пахарь

6. Коси коса пока роса

7. Золотое решето

8. Мы и сами с усами

9. Навел тень на плетень

10. Береженого Бог бережет

11. жили были дед и баба

12. Михаил Шолохов

13. Анна Каренина

14. Сергей Есенин

15. Калачи на печи

16. От топота копыт и т.п.

2 Практическое занятие №2

2.1 Тема практического занятия

Построение кодов символов некоторого алфавита. Определение избыточ­ности кода.

2.2 Цель практического занятия

Освоение методик и приобретение практических навыков построения кодов символов некоторого алфавита, а также оценки избыточности кода. Увидеть связь между количеством информации (ПЗ№1) и длиной получающихся кодов символов.

2.3 Рекомендуемая литература

1. Информатика. Базовый курс. 2-е изд. / Под ред. С.В. Симоновича. СПб.: Питер, 2007. – 640 с.

2. Брукшир Дж. Информатика и вычислительная техника. 7-е изд. – СПб.: Питер, 2004. – 620с.

3. Стариченко Б.Е. Теоретические основы информатики: Учебное пособие для вузов. – 2-е изд. – М.: Горячая линия–Телеком, 2003. – 312 с.

4. Родина Н.В. Информатика: учебное пособие, ч.1. – М.: МГУПИ, 2006. – 103 с.

2.4 Самостоятельная работа студентов при подготовке к практическому занятию

1. Ознакомиться с целями практического занятия.

2. Изучить теоретические основы, обращая особое внимание на следующие вопросы:

• Понятия «код» и «кодирование».

• Постановка задачи двоичного кодирования.

• Неравномерное кодирование.

• Префиксное неравномерное кодирование.

• Равномерное кодирование.

• Оценка избыточности кода.

2.5 Теоретический материал по теме практического занятия

Будем считать, что источник представляет информацию в форме дискретного сообщения, используя для этого алфавит, который назовем первичным.

Далее это сообщение попадает в устройство, преобразующее и представляющее его в другом алфавите – назовем его вторичным.

Код – правило, описывающее соответствие знаков или их сочетаний первичного алфавита знакам или их сочетаниям вторичного алфавита;

– набор знаков вторичного алфавита, используемый для пред­ставления знаков или их сочетаний первичного алфавита.

Кодирование – перевод информации, представляемой сообщением в первичном алфавите, в последовательность кодов.

Декодирование – операция, обратная кодированию, то есть восстановление информации в первичном алфавите по полученной последовательности кодов.

Кодер – устройство, обеспечивающее выполнение операции кодирования.

Декодер – устройство, производящее декодирование.

Операции кодирования/декодирования называются обратимыми, если их последовательное применение обеспечивает возврат к исходной информации без каких-либо потерь.

В дальнейшем будем рассматривать только обратимое кодирование.

Кодирование предшествует передаче и хранению информации.

Не обсуждая технику сторон передачи и хранения сообщения, дадим математическую постановку задачи кодирования.

Пусть первичный алфавит А состоит из N знаков со средней информацией на знак , а вторичный алфавит В – из М знаков со средней информацией на знак .

Пусть исходное сообщение, представленное в первичном алфавите, содержит n знаков, а закодированное сообщение – m знаков.

Если исходное сообщение содержит I_st(A) информации, а закодированное I_fin(B), то условие обратимости кодирования, то есть неисчезновения информации при кодировании, может быть записано следующим образом

I_st(A)  I_fin(B).

Смысл данной формулы в том, что операция обратимого кодирования может увеличить количество информации в сообщении, но не может его уменьшить.

Однако каждая из величин в данном неравенстве может быть заменена произведением числа на среднее информационное содержание знака, то есть

n   m  или .

Очевидно, что характеризует среднее число знаков вторичного алфавита, которое приходится использовать для кодирования одного знака первичного алфавита – будем называть его длиной кода или длиной кодовой цепочки и обозначим К(А,В) > 1, то есть один знак первичного алфавита представляется несколькими знаками вторичного.

Поскольку способов построения кодов при фиксированных алфавитах А и В существует множество, возникает проблема выбора наилучшего варианта – будем называть его оптимальным кодом.

Выгодность кода при передаче и хранении информации – это экономический фактор, так как более эффективный код позволяет затратить на передачу сообщения меньше энергии, а также времени, а при хранении – используется меньше площади поверхности носителя.

Минимальным возможным значением средней длины кода будет .

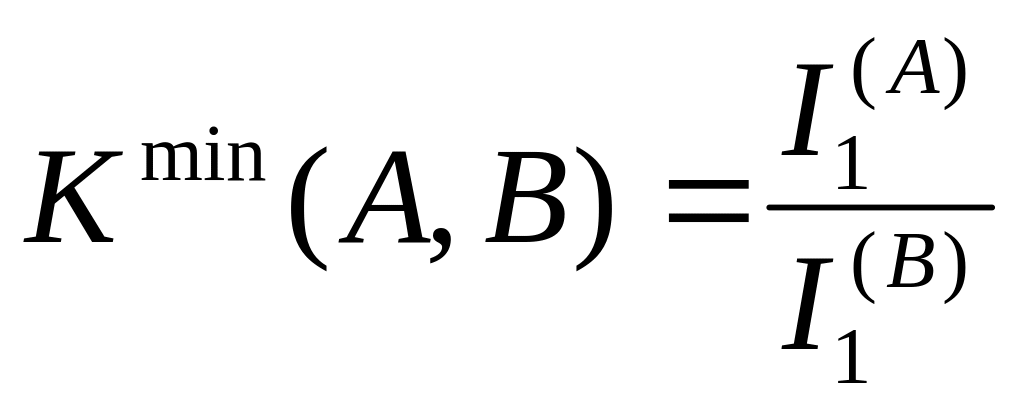Данное выражение следует воспринимать как соотношение оценочного характера, устанавливающее нижний предел длины кода, однако из него неясно в какой степени в реальных схемах кодирования возможно приближение К(А,В) к К^min (А,В).

Очевидно, что имеются два пути сокращения К^min (А,В):

– уменьшение числителя (это возможно, если при кодировании учесть различие частот появления разных знаков, их двухбуквенные, трехбуквенные корреляции (I₀ > I₁ > I₂ > … >I_n);

– увеличение знаменателя – такой способ кодирования, при котором появление знаков вторичного алфавита было бы равновероятным, то есть

I^B = log ₂ M .

В частной ситуации, рассмотренной Шенноном, при кодировании сообщения в первичном алфавите учитывается различная вероятность появления знаков, но их корреляции не отслеживаются – источники таких сообщений называются источниками без памяти.

Наиболее важной для практики оказывается ситуация, когда M=2, то есть для представления кодов в линии связи используются лишь 2 сигнала – технически это наиболее просто реализуется. Подобное кодирование называется двоичным, знаки двоичного алфавита (0,1).

При равных длительностях и вероятностях каждый элементарный сигнал несет в себе 1 бит информации I = log₂ 0,5 = 1 и тогда

K^min (A, 2) = I₁^(A) .

Шеннон сформулировал в работе «Математическая теория связи» следующую теорему:

Основная теорема о кодировании при отсутствии помех

При отсутствии помех средняя длина двоичного кода может быть сколь угодно близкой к средней информации, приходящейся на знак первичного алфавита.

Но из самой теоремы никоим образом не следует, как такое кодирование осуществить практически. Важно, что теорема открывает принципиальную возможность оптимального кодирования.

Возможны следующие особенности вторичного алфавита, используемые при кодировании:

• элементарные сигналы (0,1) могут иметь одинаковые длительности (₀ = ₁) или разные (₀  ₁);

• длина кода может быть одинаковой для всех знаков первичного алфавита (такой называется равномерным) или же коды разных знаков первичного алфавита могут иметь различную длину (неравномерный код);

• коды могут строиться для отдельного знака первичного алфавита (алфавитное кодирование) или для их комбинаций (кодирование блоков, слов).

Комбинации перечисленных особенностей определяют основу конкретного способа кодирования, однако, даже при одинаковой основе возможны различные варианты построения кодов, отличающихся своей эффективностью.

Задача оптимизации алфавитного неравномерного двоичного кодирования сигналами равной длительности

В способах кодирования, относящихся к этой группе, знаки первичного алфавита кодируются комбинациями символов двоичного алфавита (0,1), причем длина кодов и, соответственно, длительность передачи отдельного кода могут различаться. Длительности элементарных сигналов при этом одинаковы (₀ = ₁ = ).

Очевидно, для передачи информации, в среднем приходящейся на знак первичного алфавита, необходимо время К(А,2)  .

Таким образом, задачу оптимизации неравномерного кодирования можно сформулировать так:

построить такую схему кодирования, в которой суммарная длительность кодов при передаче (или суммарное число кодов при их хранении) данного сообщения была бы наименьшей.

За счет чего возможна такая оптимизация? Очевидно, суммарная длительность сообщения будет меньше, если применить следующий подход: тем знакам первичного алфавита, которые встречаются в сообщении чаще, присвоить меньшие по длине коды, а тем, относительная частота которых меньше – коды более длинные.

Параллельно должна решаться проблема различимости кодов. Представим, что на выходе кодера получена следующая последовательность сигналов «0010001000011101010111000011» .

Каким образом она может быть декодирована? Если бы код был равномерным, приемное устройство просто считывало бы заданное (фиксированное) число элементарных сигналов и интерпретировало их в соответствии с кодовой таблицей.

При использовании неравномерного кодирования возможны 2 подхода к обеспечению различимости кодов:

• используется специальная комбинация элементарных сигналов, которая интерпретируется декодером как разделитель знаков;

• применяются префиксные коды.

Префиксное неравномерное кодирование

Возможно ли такое кодирование, которое не использует разделители? Существует ли оптимальный способ неравномерного двоичного кодирования?

Суть первого вопроса состоит в нахождении такого варианта кодирования, при котором последующее выделение из него каждого отдельного знака оказывается однозначным без специальных указателей разделения знаков.

Наиболее простыми и употребимыми кодами такого типа являются так называемые префиксные коды, которые удовлетворяют следующему условию Фано.

Неравномерный код может быть однозначно декодирован, если никакой из кодов не совпадает с началом (префиксом) какого-либо иного более длинного кода.

Например, если имеется код 110, то уже не могут использоваться коды 11, 1, 1101, 11001, и т.п.

Если условие Фано выполняется, то при прочтении (расшифровке) закодированного сообщения путем сопоставления с таблицей кодов всегда можно точно указать, где заканчивается один код и начинается другой.

Наиболее известны 2 схемы построения префиксных кодов:

• префиксный код Шеннона – Фано;

• префиксный код Хаффмана.

Пример построения префиксного кода Шеннона – Фано

Шенноновский источник порождает множество шестизначных сообщений, каждое из которых содержит 1 знак «*», 2 знака «%» и 3 знака «!» (ПЗ№1). Построить код Шеннона-Фано и оценить его избыточность.

Решение задачи.

1. Определим вероятность (относительную частоту) появления каждого символа. Они равны соответственно

р_*=1/6, р_%=2/6, р_!=3/6.

Расположим символы в таблицу в порядке убывания частот.

Символ	рсимв	1 шаг	2 шаг	Код Шеннона-Фано
!	3/6	0		0
%	2/6	1	0	10
*	1/6	1	1	11

Делим множество символов на 2 группы, соблюдая примерное равенство суммы вероятностей для каждой группы. Деление на группы в таблице выделяем жирными обрамляющими линиями. Условимся символ, попавший в верхнюю группу, обозначать 0, в нижнюю – 1.

Деление выполняется для каждой группы с соблюдением указанного условия, пока количество элементов в каждой группе не станет равным 1. Получившаяся запись из 0 и 1 в строке каждого символа и составляет его код.

Для нашего задания

код ! – «0», код % – «10», код * – «11».

2. Оценим избыточность кода. В среднем на один символ приходится (ПЗ №1) I_ср= 1.459 бит.

Средняя длина кода

К_ср= К_!*р_! + К_%*р_% + К_**р_* = 1*3/6 + 2*2/6 + 2*1/6 = 1.5

Избыточность кода равна R= К_ср/I_ср – 1 = 1.5 / 1.459 – 1 = 0.0281 (2.83%)

Вероятность 0 и 1 в кодах равны соответственно р₀= 2/5, р₁=3/5.

3. Длина кода для передачи всего сообщения будет равна 9 разрядам (что достаточно близко к I _сообщ = I_ср * 6 = 8.755 бит).

Пример построения префиксного кода Хаффмана

Дан первичный алфавит из 6 символов А=(а₁, а₂, а₃, а₄, а₅, а₆) с вероятностями (0.30, 0.20, 0.20, 0.15, 0.10, 0.05) соответственно.

Решение задачи.

Создадим новый алфавит А1, объединив 2 знака с наименьшими вероятностями (а₅, а₆), и заменив их новым знаком а⁽¹⁾. Вероятность нового знака равна сумме вероятностей тех знаков, что в него вошли, то есть 0.15. остальные знаки алфавита включим в новый без изменений. Общее число знаков будет на 1 меньше, чем в исходном.

Аналогичным образом продолжим создавать новые алфавиты, пока в последнем на останется 2 знака. Очевидно, что количество шагов будет равно (N-2), где N – число знаков исходного алфавита.

В промежуточных алфавитах каждый раз будем переупорядочивать знаки по убыванию вероятностей.

Всю процедуру построения представим в виде таблицы 2.

Таблица 2

№ знака	Исх. алф-т А	А(1)	А(2)	А(3)	А(4)
1	0 .3	0 .3	0 .3	0 .4	0.6
2	0 .2	0 .2	0 .3	0 .3	0.4
3	0 .2	0 .2	0 .2	0.3
4	0 .15	0 .15	0.2
5	0 .10	0.15
6	0.05

Теперь в обратном направлении (против стрелок) проведем процедуру кодирования. Двум знакам последнего алфавита присвоим коды 0 и 1 (которому какой – роли не играет; например, условимся, что верхнему – 0, а нижнему –1). Процесс кодирования представлен в таблице 3.

Таблица 3 Построение кода Хаффмана

№ знака	Исх. алф-т А		А(1)		А(2)		А(3)		А(4)
	вер-сть	коды	вер-сть	коды	вер-сть	коды	вер-сть	коды	вер-сть	коды
1	0.30	0 0	0 .3	0 0	0.3	0 0	0.4	1	0.6	0
2	0.20	1 0	0 .2	1 0	0 .3	0 1	0.3	0 0	0.4	1
3	0.20	1 1	0 .2	1 1	0 .2	10	0.3	01
4	0.15	0 10	0 .15	010	0 .2	11
5	0.10	0 110	0 .15	011
6	0.05	0111

Средняя длина кода равна:

2*(0.30+0.20+0.20)+3*0.15+4*(0.10+0.05)=2.45.

Избыточность равна 0.0249. Вероятности 0 и 1 соответственно равны 0.47 и 0.53.

Пример построения равномерного кода

Шенноновский источник порождает множество шестизначных сообщений, каждое из которых содержит 1 знак «*», 2 знака «%» и 3 знака «!» (ПЗ№1). Построить равномерный код и оценить его избыточность.

Решение задачи.

1. Количество двоичных символов для равномерного кодирования k = log₂3 = 1.585 = 2 , так как k – целое число.

Возможный вариант кодирования

! – 00

% – 01

* – 11

2. Очевидно, что средняя длина кода К_ср = 2.

Длина всего сообщения К_сообщ = 2*6 = 12 разрядов.

3. Избыточность кода соответственно равна

Q = К_ср/I_ср – 1 = 2 / 1.459 – 1 = 0.370 (37%)

Вероятности 0 и 1 равны между собой (3/6).