Бородавкин В.А., Петрова И.Л. ТАУ дискретных систем / 10 Лекция

6

Лекция 10.

Устойчивость импульсных систем.

10.1 Критерии устойчивости.

Аналог критерия устойчивости Найквиста.

Существует также аналог критерия устойчивости Найквиста для импульсных систем. Дадим его вывод.

Возьмем передаточную функцию разомкнутой цепи импульсной системы

где N^* и L^* - многочлены по e^q степени k и m>k.

Положим

Обозначим

(1)

Возьмем вспомогательную функцию

(2)

где H(z) – характеристический многочлен замкнутой системы, а - разомкнутой.

По аналогу критерия Михайлова в случае устойчивой разомкнутой цепи имеем

(аргумент комплексного числа)

Для устойчивости же замкнутой системы требуется чтобы

В результате получаем требование

т.е. годограф вспомогательной функции F не должен охватывать начало координат.

Отсюда, переходя согласно (2) к функции , получаем формулировку аналога критерия Найквиста: если разомкнутая цепь устойчива, то для устойчивости замкнутой системы требуется, чтобы амплитудно-фазовая частотная характеристика разомкнутой цепи не охватывала точку (-1).

В случае нейтральной разомкнутой цепи, т.е. при наличии в многочлене L^*(q) корня q=0 или в корня z=1 (рис.6), нужно обходить контур, минуя точку z=1, по четверти окружности малого радиуса r, как показано на рис.6.

r

0 z=1

Рис.6.

Учитывая в выражении (1) полюс z=1, можно записать

где представляет собой оставшуюся часть исходной функции после выделения в знаменателе множителя (z-1), соответствующего полюсу z=1.

Вместо z=1 введем согласно рис.6

После этой подстановки получаем

где

Обратимся к случаю неустойчивой разомкнутой цепи, когда передаточная функция содержит р полюсов вне единичного круга. Тогда в выражениях (1) и (2) по принципу аргумента

а для устойчивости замкнутой системы, по-прежнему, требуется

Поэтому изменение аргумента выражения (2) должно удовлетворять соотношению

Следовательно, для устойчивости замкнутой системы при неустойчивой разомкнутой цепи требуется, чтобы амплитудно-фазовая характеристика разомкнутой цепи охватывала точку (-1) на угол (против часовой стрелки), где р – число полюсов , лежащих вне единичного круга .

Пример показан на рис.7 для случая р=2.

-1 0

Рис.7

Для исследования устойчивости импульсных систем могут применяться также логарифмические частотные характеристики.

Аналог критерия устойчивости Гурвица.

Основной причиной, не позволяющей применять алгебраический критерий устойчивости Гурвица для анализа устойчивости дискретных САУ, является то, что в плоскости р характеристический полином замкнутой системы является трансцендентной функцией от комплексной переменной р. Используя совместно z- и w – ппреобразования, можно трансцендентную функцию от р преобразовать в полином от w. При этом левая полуплоскость плоскости р отображается в левую полуплоскость плоскости w и условия устойчивости полностью совпадают с условиями устойчивости Гурвица для непрерывных систем.

Пусть характеристический полином замкнутой системы имеет вид

После подстановки и выполнения ряда преобразований (аналогично форм.(5), (6) Лекции 9 ) получим

(3)

где b_i – новые коэффициенты уравнения.

К характеристическому уравнению (3) можно применить обычный критерий Гурвица. Необходимое и достаточное условия устойчивости САУ состоят в том, что при b₀>0 все определители Гурвица должны быть положительными, т.е. , где (k=1,2,3,…,n).

Пример.

Для ДАС с характеристическим уравнением

Билинейное преобразование дает

В этом случае условия устойчивости принимают вид

(4)

Если ДАС имеет высокий порядок, то помимо трудностей, связанных с применением алгебраических критериев устойчивости, возникают дополнительные трудности, вызванные расчетами коэффициентов уравнения (3).

К основным недостаткам алгебраических критериев следует отнести трудоемкость вычислений определителей для нахождения условий устойчивости, отсутствие связи с экспериментальными методами исследования ДАС, а также то, что они не дают ответа на вопрос, как изменить параметры ДАС, чтобы обеспечить ее устойчивость.

10.2 Оценка устойчивости по логарифмическим псевдочастотным характеристикам (ЛПЧХ).

Применение w - преобразования и понятия псевдочастот позволяет строить ЛПЧХ разомкнутой дискретной САУ. Эти характеристики могут быть использованы для оценки устойчивости ДАС, как это делалось при исследовании систем непрерывного действия. Построение ЛПЧХ производятся аналогично правилам построения ЛАХ и ЛФЧХ для САУ непрерывного действия. Отличительной особенностью ЛПЧХ является наличие дополнительных сомножителей в числителе вида , что соответствует системе неминимально-фазового типа.

Пример.

Рассмотрим импульсную систему первого порядка, состоящую из экстраполятора нулевого порядка и непрерывной части. Передаточная функция непрерывной части имеет вид

.

Передаточная функция приведенной непрерывной части имеет вид

Используя z-преобразование, получим выражение дискретной передаточной функции разомкнутой системы:

Полагая , определим амплитудно-фазовую частотную характеристику импульсной САУ:

(5)

Как следует из выражения (5), и

(гиперболический тангенс)

Эта частотная характеристика изображена на рис.8. Замкнутая импульсная система будет устойчива, если точка не будет охватываться кривой

, т.е. если (гиперболический котангенс)

Отсюда следует вывод:

В отличие от непрерывных САУ, описываемых дифференциальными уравнениями 1-го и 2-го порядка, устойчивых при любых положительных значениях коэффициента усиления. Дискретные САУ 1-го и 2-го порядка всегда имеют предельный коэффициент усиления, превышение которого приводит к неустойчивости.

10.3 Области устойчивости дискретных систем.

При анализе и синтезе дискретных систем часто требуется выявить влияние числовых значений каких-либо варьируемых параметров на устойчивость. Обычно этими параметрами являются постоянные времени и коэффициенты усиления.

Определим область устойчивости в плоскости параметров для системы, рассмотренной в предыдущем примере.

Характеристический полином замкнутой импульсной системы имеет вид

где

Согласно условию устойчивости (модуль зет ф.4 из лекции 9) необходимо, чтобы и . Пользуясь этими неравенствами, получаем

Граничные кривые могут быть получены при замене этих неравенств на равенства. В этом случае из первого выражения следует:

из второго

Область устойчивости в плоскости параметров () находится между этими границами (рис.9).

Область неустойчивости

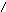
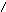
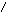
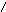
0

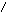
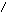
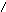
-1 Область устойчивости

рис.9