

& |
|
|
|
|
|
|
|
|
|
|
|
|
|
px(p) = Ax(p) + Bu(p), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
о[x]= о[Ax + Bu], |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
о[y]= о[Cx]. |
|
|
|
|
y(p) = Cx(p). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(pI − A)x(p) = Bu(p) |
→ x(p) = (pI − A)−1 Bu(p) |
|
|
|
|
||||||||||||||||||||||||||||||||||||
или |
|
|
|
|
|
|
|
y(p) = C(pI − A)−1 Bu(p), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
W(p) = |
y(p) |
|
= C(pI − A)−1 B. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
u(p) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
& |
= x2 , |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
1 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
x1 |
|
|
|
|
|
|
|
|
A= |
|
B = |
C = [1 0]. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
& |
= x1 |
+ x2 |
|
|
+ 2u, |
|
|
; |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
x2 |
|
|
|
|
|
|
1 |
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
y = Cx1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
W(p) = |
y(p) |
|
= C(pI − A)−1 B; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
u(p) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
pI − A= |
|
p |
|
|
0 |
0 |
|
1 |
|
p |
− 1 |
|
det(pI − |
A) = p |
2 |
|
− p− 1. |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
0 |
|
|
p − |
1 |
|
1 = − 1 |
p |
− 1 ; |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
(pI − A) |
−1 |
= |
|
|
|
1 |
|
|
|
|
p −1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
; |
где i, j |
элемент получен из выражения |
|
|||||||||||||||||||||||||||||||||
|
|
det(pI − |
|
|
|
1 |
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
A) |
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
[(−1)i+ j |
|
|
Mij |
], Mij – минор i, j элементов. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
W(p) = 1 0 |
|
|
|
|
1 |
|
|
|
|
|
|
p −1 |
1 0 |
= |
|
|
|
1 |
|
|
[ |
p − |
1 1 |
0 |
= |
|
|
2 |
|
; |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
2 |
|
|
|||||||||||||||||||||||||
|
[ |
|
|
|
|
] |
|
det(pI |
|
|
|
|
|
|
|
p 2 |
|
p |
|
− p − |
1 |
|
|
|
|
|
|
|
] 2 |
|
p |
− p −1 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
− A) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
det(pI − A) =ϕ(p) – характеристический полином системы; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
det(pI − A) =ϕ(p) = 0 – характеристическое уравнение системы. |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
Передаточная функция скалярных систем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
Имеем дифференциальное уравнение, описывающее поведение скалярной системы |
(1) |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
(n) |
|
|
|
|
|
|
(n−1) |
|
|
|
|
|
|
& |
|
|
|
|
(m) |
|
|
|
|
(m−1) |
|
|
|
|
|
|
|
|
|
|
||||||||
|
an x + an−1x |
|
|
|
|
|
|
|
|
|
|
= bmu + bm−1u |
|
|
|
|
+ Κ + b0u. |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
+ Κ + a1x |
+ a0 x |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
Используя свойства преобразования Лапласа перепишем (1) в изображениях |
|
|
(2) |
|||||||||||||||||||||||||||||||||||||||||||
(an pn + an−1 pn−1 |
|
+ Κ |
|
+ a1 p+ a0 )x(p) = (bm pm + bm−1 pm−1 + Κ |
+ b0 )u(p). |
|||||||||||||||||||||||||||||||||||||||||
По определению, тогда передаточная функция |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x(p) |
|
|
|
|
b pm + b |
pm−1 + Κ + b |
|
|
|
|
|
|
|
B(p) |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
W(p) = |
|
|
|
|
|
= |
|
|
m |
|
|
m−1 |
|
|
|
|
|
|
0 |
|
|
|
= |
|
|
|
, |
|
|
|
|
|
(3) |
|||||||
|
|
|
|
|
|
|
u(p) |
|
an pn + an−1 pn−1 + Κ + a1 p + a0 |
|
|
A(p) |
|
|
|
|
|
|||||||||||||||||||||||||||||
где A(p), B(p) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
– соответственно полиномы знаменателя и числителя передаточной функции. |
|||||||||||||||||||||||||||||||||||||||||||||
В ТАУ W(p) принято записывать в нормированном виде, когда свободные члены в полиномах A(p) и B(p) равны 1.
где b0 = k a0
Пример:
|
|
|
|
|
bm |
|
pm + |
bm−1 |
pm−1 + Κ +1 |
|
|||||
|
b |
|
|
b |
b |
(4) |
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||
Wн (p) = |
|
0 |
|
|
0 |
|
|
0 |
|
|
|
|
, |
||
a |
|
|
|
an |
|
|
an−1 |
− |
|
|
|
||||
|
|
0 |
|
|
|
|
|
pn + |
|
pn |
1 |
+ |
Κ +1 |
|
|
|
|
|
|
|
a0 |
|
a0 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
– коэффициент передачи (усиления) элемента или системы.
& |
= x2 , |
|
& |
|
& |
& & |
x1 |
|
= x1 |
||||
& |
= x1 + x2 |
+ 2u. |
x1 |
+ x1 |
+ 2u x − x − x = 2u. |
|
x2 |
|
|
|
|
По свойствам преобразования Лапласа найдем
17

(p2 − p− 1)x(p) = 2u(p).
Итак, W(p) = x(p) = 2 . u(p) p2 − p −1
Имея передаточную функцию на структурных схемах, связь между входом u(p) и выходом y(p) можно показать в виде (рис.18).
u(p) |
|
y(p) |
|||
W(p) |
|||||
|
|
|
|
||
|
|
|
|
|
|
|
|
рис. 18 |
|||
Частотные характеристики САУ
При исследовании и создании САУ, аппарат частотных характеристик был одним из первых, т.к. они наиболее полно отражают физическую природу процессов, происходящих в динамических объектах.
В качестве преобразования функции f(t) используется преобразование Фурье
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
F(jω) = ∫ f (t)e− jωt dt . |
(1) |
|
|
|
|
|
|
|
−∞ |
|
Преобразование Фурье |
позволяет |
разложить непериодическую |
функцию f(t) для которой |
||||
выполняется условие сходимости |
|
|
|||||
∞ |
|
|
|
|
|
||
∫ |
|
|
f (t) |
|
dt < ∞ |
(интеграл существует) |
(2) |
|
|
||||||
−∞
в бесконечный ряд гармоник, образующих непрерывный спектр частот в интервале от –∞ до +∞ с бесконечно малым интервалом частот между смежными частотами (∆ω → 0).
Отметим, что по сравнению с преобразованием Лапласа преобразование Фурье позволяет отобразить оригинал только на мнимую ось, в преобразовании Лапласа же используется вся комплексная плоскость.
Для перехода к частотным характеристикам, необходимо в уравнение ПФ (3) (стр.17) вместо оператора Лапласа p подставить оператор Фурье jω (p→jω), получим частотную характеристику
|
X( jω) |
|
b ( jω)m + b |
( jω)m−1 + b |
( jω)m−2 + Κ + b |
|
||
W( jω) = |
|
= |
m |
m−1 |
m−2 |
0 |
. |
(3) |
F( jω) |
|
|
|
|
||||
|
|
an ( jω)n + an−1( jω)n−1 + an−2 ( jω)n−2 + Κ + a0 |
|
|||||
Рассмотрим понятие о частотных характеристиках.
Если на вход линейной разомкнутой системы (или звена) подать гармонический входной сигнал, то по истечении некоторого времени окончания переходных процессов на выходе системы (звена) установится также гармонический выходной сигнал той же частоты. Амплитуда и фаза при прочих равных условиях будут зависеть от частоты входного сигнала. По ним, как будет показано дальше, можно судить о свойствах САУ.
Достоинством частотных методов является то, что частотные характеристики можно снять экспериментально. Чтобы снять частотную характеристику необходимо на вход подавать гармонический сигнал, изменяя частоту от 0 до ∞, а на выходе измерять амплитуду и фазу для частот ωi.
Отметим еще, что в выражении передаточной функции и частотной характеристики для реальных систем степень знаменателя всегда больше степени числителя n>m, т.к. полоса пропускания частот реальной системы всегда ограничена. Действительно, если n<m, то на выходе системы при увеличении частоты могут возникнуть колебания с бесконечно большой амплитудой.
Частотная характеристика (ЧХ) элемента или системы W(jω) может быть представлена в двух видах:
1.W(jω) = P(ω) + jQ(ω),
2.W( jω) = A(ω)ejϕ(ω) .
где P(ω) – вещественно-частотная характеристика (ВЧХ); Q(ω) – мнимо-частотная характеристика (МЧХ); A(ω) – амплитудно-частотная характеристика (АЧХ);
18
ϕ(ω) – фазо-частотная характеристика (ФЧХ).
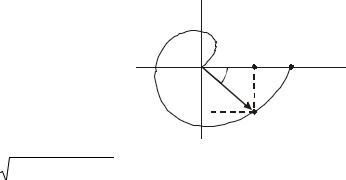
Часто ЧХ представляется графически (рис.19) на комплексной плоскости, где все указанные величины связаны между собой по следующим соотношениям.
Q(ωi)
Q(ω)[Im] |
|
ω=∞ P(ωi) ω=0 |
P(ω)[Re] |
ϕ(ωi) |
|
A |
|
( |
|
ω |
|
i) |
|
ωi |
|
|
|
|
|
Рис.19 |
A(ω) = P2 (ω) + Q2 (ω) |
– АЧХ. |
|||
ϕ(ω) = arg W(jω) |
] |
= arctg |
Q(ω) |
– ФЧХ. |
|
||||
[ |
|
P(ω) |
|
|
|
|
|
|
|
Часто при исследовании систем используются логарифмические частотные характеристики.
Понятие о логарифмических частотных характеристиках
При исследовании САУ, амплитудную и фазовую частотные характеристики удобно строить в логарифмических координатах. Это связано с двумя обстоятельствами:
1.в логарифмических масштабах кривизна характеристик резко уменьшается, что позволяет в большинстве практических случаев приближенно изображать АЧХ ломанными линиями.
2.в логарифмических масштабах АЧХ цепочки звеньев равна сумме АЧХ отдельных звеньев
n
lg A = ∑lg Ai .
i=1
АЧХ в логарифмических масштабах строится в координатах 20lgA и lgω, а ФЧХ – в виде зависимости ϕ от lgω.
Единицей измерения 20lgA служит децибел, равная 0,1 бела. Бел – единица измерения десятичного логарифма коэффициента усиления мощности сигнала, т.е. 1 бел соответствует усилению мощности в 10 раз, 2 бела – в 100 раз и т.д. Так как мощность сигнала пропорциональна квадрату амплитуды A2
(Пример: для электрической цепи P = I 2R; P ≡ I 2 ), lg A2 = 2 lg A, то усиление в белах, выраженное
через отношение амплитуд |
|
|
|
A, |
|
|
|
|
|
равно |
|
2 lg A, |
|
соответственно |
в децибелах оно равно |
||||||||||||||||||||||||||
2 10 lg A = 20 lg A. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
20 lgA |
|
|
|
[дб] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
30 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 78910 |
|
100 |
|
1000 |
ω[c–1] |
||||||||||||||||||
|
|
1 |
2 |
|
3 |
4 |
5 |
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
3 |
lg ω (декады) |
|||||||||||||||||||
–45° |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
3 4 |
5 6 |
|
|
7 |
8 9 10 |
log2 ω (октавы) |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
–90° |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–ϕ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис.20 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
По оси абсцисс откладывается в логарифмическом масштабе частота lgω (десятичный логарифм)
(изменение частоты в 10 раз – декада), а около отметок указывается само значение частоты. Иногда применяется логарифм частоты при основании 2 (изменение частоты в два раза – октава) одна октава равно 0,303 декады, т.к. lg2= 0,303.
19
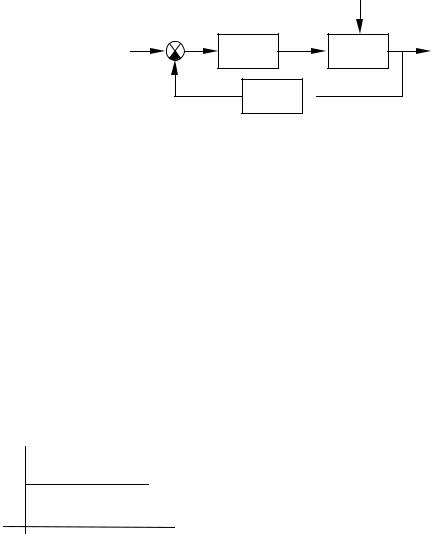
Для построения логарифмических фазовых характеристик (ЛФХ) на оси абсцисс используется аналогичная шкала частот lgω или log2 ω , а по оси ординат (обычно используется нижняя часть
плоскости) откладывается фаза ϕ в градусах.
Отметим ещё, т.к. точка ω = 0 в логарифмическом масштабе находится слева (в –∞), то ЛАФХ строятся не от ω = 0, а от достаточно малого, но конечного значения ω , которое и откладывается в начале координат.
Структурные методы ТАУ
Математическое описание САУ начинается с разбиения её на типовые по математическому описанию звенья. По уравнениям или характеристикам отдельных звеньев составляются уравнения или характеристики системы в целом. Разбиение на типовые звенья по математическому описанию позволяет перейти от необозримого множества физических элементов к конечному числу звеньев.
Структурная схема САУ составляется из типовых звеньев направленного действия. Звеном направленного действия называется звено, которое передает воздействие только в одном направлении со входа на выход (рис.21).
F(p)
u3(p) E(p) Wy(p) uy(p) Woy(p) x(p)
uoc(p)
Wос(p) 
рис. 21
Получение структурной схемы в большинстве случаев является конечной целью математического описания системы.
Типовые звенья САУ
Ктиповым по математическому описанию звеньям САУ относятся:
1.Усилительное;
2.Интегрирующее;
3.Апериодическое;
4.Колебательное или звено второго порядка;
5.Идеальное дифференцирующее;
6.Реальное дифференцирующее.
Вначале рассмотрим стандартные сигналы, действующие при расчетах систем: 1. Единичный ступенчатый сигнал (рис.22).
g(t) |
0, |
при t < 0, |
|
|
|||
1 |
g(t) = |
1, при t ≥ 0 |
|
|
|||
Рис.22 t
Основной сигнал при котором исследуются САУ. Это наиболее тяжелый в смысле влияния на систему сигнал. Реально на систему чаще действуют сигналы постепенно возрастающие во времени. Следовательно, при удовлетворительной работе системы при единичном сигнале, она будет работать лучше при сигнале, отличном от единичного.
20

2.Единичный импульсный сигнал (рис.23), получается дифференцированием единичной ступенчатой функции, называемой δ(t)– дельта функцией.
δ(t)
0,•рЏ t ≠ 0, δ(t) =
∞,•рЏ t = 0.
Рис.23 t
Единичный импульс – это математическая идеализация предельно короткого импульсного сигнала. Единичный импульс – это импульс, площадь которого равна единице при длительности равной нулю и высоте, равной бесконечности.
∞
∫δ(t)dt = 1.
−∞
3. Гармонический сигнал.
Определения:
1.Реакция звена или системы на единичный ступенчатый сигнал, называется переходной функцией (характеристикой).
2.Реакция звена или системы на δ-функцию называется импульсно-переходной функцией.
3. Реакция звена или системы на гармонический сигнал при изменении частоты от 0 до ∞ (0≤ω ≤ ∞) , называется частотной характеристикой.
При рассмотрении всех типовых звеньев нас будут интересовать такие характеристики:
1.Определение и математическое описание звена.
2.Передаточная функция.
3.Реакция звена на стандартные сигналы:
3.1.Переходная функция.
3.2.Импульсно-переходная функция.
3.3.Частотная характеристика.
3.3.1.в обычном масштабе.
3.3.2.в логарифмическом масштабе.
4.Примеры.
1.Усилительное звено
1.Безынерционное звено, сигнал на выходе которого строго пропорционален сигналу на входе, называется усилительным звеном (рис.24).
g(t) |
УЗ |
x(t) |
По определению x(t) = k g(t), |
|
|
|
|
|
g(t) – входное воздействие (один из стандартных сигналов), |
|
|
|
|
|
|
|
рис. 24 |
|
x(t) – реакция на выходе, |
k– коэффициент пропорциональности.
2.Переходя к преобразованию Лапласа X(p) = kQ(p), тогда передаточная функция:
X(p)
W(p) = Q(p) = k ,
k – коэффициент усиления (если величина безразмерная) и коэффициент передачи (если k размерно).
3.1. Если на вход усилительного звена подать единичную ступенчатую функцию g(t), то переходная функция будет иметь вид, как показано на рис.25.
21

g(t) |
|
|
x(t) |
x(t) |
|
|
|
|
|
g(t) |
|
|
k |
|
|
|
1 |
t |
|
|
|
||
|
|
|
|
|
Рис.25 |
|
|
3.2.Для получения импульсной переходной функции необходимо продифференцировать по времени переходную характеристику, тогда на выходе имеем δ(t)-функцию.
3.3.Частотная характеристика ( p→ jω ).
|
X( jω) |
P(ω) = k, |
ω |
= |
k, |
|
3.3.1. W( jω) = |
|
= k, |
A( ) |
|
||
|
Q(ω) = 0, |
ϕ(ω) = 0ο |
||||
Q( jω) |
||||||
на комплексной плоскости имеет вид:
Im
K
Re
Рис.26
3.3.2. ЛЧХ: 20 lgA(ω) = 20 lgk .
20 lgA(ω) |
|
|
|
|
20 lgA(ω) |
|
|||
|
|
|
|
||||||
20 lgk |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||
|
|
|
1 |
10 |
100 ϕ(ω) ω |
||||
|
|
|
|
|
|
|
|
|
lgω |
|
|
|
0 |
1 |
2 |
|
|||
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
Рис.27
ЛФХ: ϕ(ω) = 0.
Описание реальных элементов динамическими характеристиками усилительного безинерционного звена является всегда некоторой идеализацией, т.к. все реальные объекты в природе – инерционны.
4.
1.
|
|
|
|
|
|
|
iвых |
iвых = |
1 |
Uвх |
= kUвх , где |
k = |
1 |
(1/ом) |
– коэффициент передачи. |
||||||||||||||||
Uвх |
|
|
|
|
R |
R |
R |
||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. |
|
|
|
R1 |
|
|
|
|
|
|
R2 |
|
|
|
|
|
|
|
|
|
|
R2 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
вых |
= |
|
|
U |
вх |
= kU |
вх |
, |
где k = |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Uвх |
|
|
|
|
|
|
|
|
Uвх |
|
R |
+ R |
2 |
R |
+ R |
2 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
R2 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
– коэффициент усиления. |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.Интегрирующее звено
1.Звено, сигнал на выходе которого пропорционален интегралу от входного сигнала, называется интегрирующим звеном.
τ
По определению: x(t) = ∫g(t)dt .
0
22
g(t) |
ИЗ |
x(t) |
|
|
рис. 28
2. Из свойства преобразования Лапласа:
1 |
|
k |
||
X(p) = k |
|
Q(p) = |
|
Q(p). |
p |
p |
|||
Тогда по определению передаточная функция будет
X(p) k W(p) = Q(p) = p .
Отметим, что коэффициент передачи интегрирующего звена имеет размерность 1/сек.
3.1. Если g(t) – единичная ступенчатая функция, то переходная функция интегрирующего звена имеет вид x(t) = kt (рис.29).
|
|
g(t) |
δвых(t) |
x(t)=kt |
|
|
|
|
x(t) |
|
|
δвых(t)=k |
|
|
|
|
|
|
||
|
|
|
|
k |
g(t) |
|
|
|
|
|
|
|
|
|
|
|
|
arctg k |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
Рис.29 |
|
t |
|
|
|
|
|
|
|
3.2. Если g(t) =δ(t), то дифференцируя x(t), получим δвых (t) = k |
(рис.29). |
|||||
3.3. Частотная характеристика. |
k |
|
|
|
||
X(jω) |
k |
= − j |
|
|
|
|
3.3.1. W(jω) = Q(jω) = |
jω |
ω , |
|
|
|
|
P(ω) = |
|
k |
A(ω) = |
k |
||
|
ω , |
|||||
0, |
|
|
|
|
||
|
ϕ(ω) = −π |
|||||
Q(ω) = − |
|
, |
||||
ω |
||||||
|
|
|
|
|
2 |
|
т.е. амплитудно-фазовая характеристика при изменении частоты от 0 до ∞ проходит по отрицательной мнимой оси комплексной плоскости (рис.30).
Im
ω=∞
0 |
Re |
W(jω) ω→∞
|
Рис.30 |
3.3.2. ЛАХ: |
20lg A(ω) = 20lgk − 20lgω . |
Вычислим значение ЛАХ при ω = 1и ω =10. |
|
ω = 1, |
20lg A(1) = 20lgk , |
ω =10, |
20lg A(10) = 20lgk − 20. |
Следовательно, при изменении частоты на 1 декаду, амплитуда уменьшается на 20 децибел (рис.31).
23
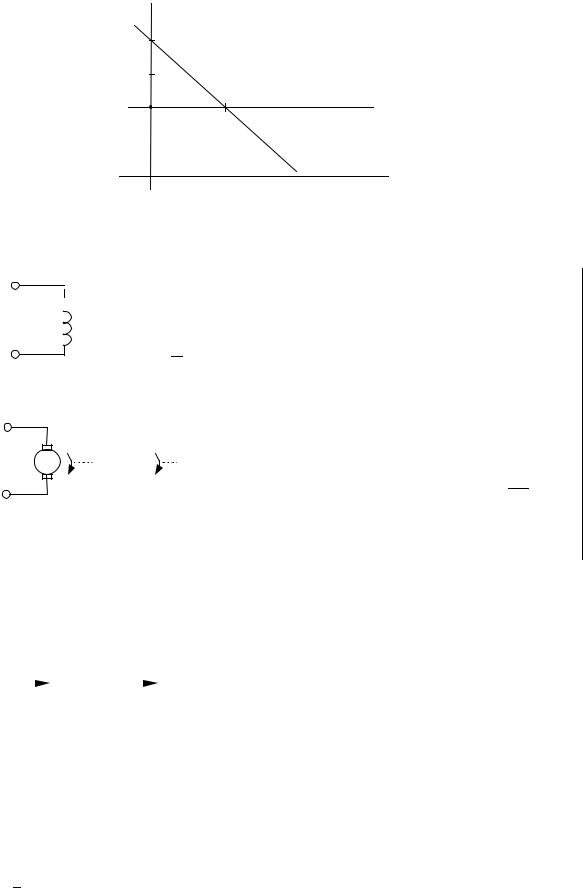
20lgA |
|
|
||
20 |
|
|
20lgk, где k=10 |
|
10 |
|
|
|
|
1 |
10 |
ω |
||
0 |
2 |
lgω |
||
–π/4 |
|
|
|
–20 дб/дек |
|
|
|
|
|
|
|
ЛАХ |
–π/2 |
|
ЛФХ |
|
|
ϕРис.31
π
ЛФХ: ϕ(ω) = − 2
4.
1.
 iвых
iвых
Uвх L
если R=0, то по закону Кирхгофа |
|
|||||
|
di |
|
1 |
T |
T |
|
Uвх = L |
вых |
; |
iвых = |
|
∫Uвхdt = k∫Uвхdt , |
|
|
L |
|||||
|
dt |
|
0 |
0 |
||
1
k = L (1/Гн) – коэффициент передачи.
2.
|
|
|
|
|
ω |
|
θ |
|
|
|
|
|
Д |
Ред. |
Нагр. |
||||||
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
T |
|
|
|
|
|
|||
θ = |
∫ωdt, k – коэффициент передачи редуктора. |
|||||||||
k |
||||||||||
|
0 |
|
|
|
|
|
|
|
||
ω – угловая скорость вращения вала двигателя. θ – угол поворота выходного вала редуктора. Для редуктора g(t) =ω, x(t) =θ .
dθ
Из механики известно, что ω = k dt , тогда
3.Апериодическое (инерционное) звено или звено 1-го порядка
1.Звено, которое описывается уравнением вида:
g(t) |
|
|
x(t) |
|
dx(t) |
||
АЗ |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
T dt + x(t) = kg(t), |
|||
|
|
|
|
|
|||
где k – коэффициент передачи (усиления),
T– постоянная времени, характеризующая
инерционность (с), называется апериодическим звеном. |
|
|||||
2. Переходя к преобразованию Лапласа |
|
|
|
|
||
(Tp+1)x(p) = kG(p) |
(1) |
|||||
получим по определению передаточную функцию |
|
|||||
|
x(p) |
|
k |
|
(2) |
|
W(p) = G(p) = Tp +1 |
||||||
g(t) = 1 представляет собой экспоненту |
||||||
3.1 Переходная характеристика такого |
звена при |
|||||
t
x(t) = k(1− e− T ).
24
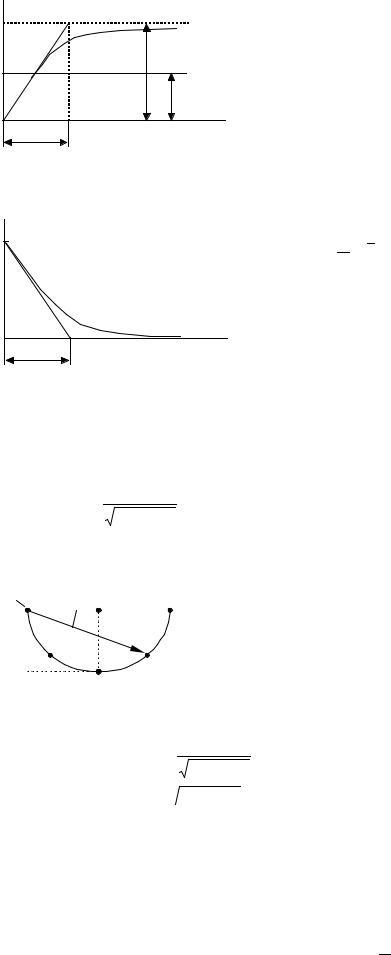
g(t) |
|
|
|
|
|
|
|
xуст |
|
x(t) |
Переходный |
процесс |
достигает |
своего |
|
|
|
|
|||||
|
|
|
|
||||
|
|
k |
g(t) |
установившегося значения 0,95xуст практически за 3T |
|||
|
|
|
(рис.33). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
T |
Рис.33 |
t |
|
|
|
|
|
|
|
|
|
|
|
|
3.2 |
Импульсная переходная функция при |
g(t) =δ(t) находится дифференцированием |
x(t) при |
||||
g(t) = 1, получим |
|
|
|
|
|
|
|
g(t) |
|
k/T |
|
T |
t |
|
Рис.34 |
k− t
δвых (t) = T e T (рис.34.)
Если эти характеристики получены экспериментально, то по ним можно определить T и k, как показано на рис. 33 и 34, и, таким образом, получить уравнение звена (что очень важно).
|
|
|
|
|
|
|
|
|
|
3.3.1 Частотная характеристика: |
||||||
|
|
|
W(jω) = |
x(jω) |
|
k •(1− jTω) |
k − jkTω |
|
|
|||||||
|
|
|
|
|
= |
|
|
|
= |
|
|
|
; |
|
||
|
|
|
G(jω) |
Tjω + 1 |
|
T2ω 2 + 1 |
|
|||||||||
|
|
|
|
|
|
•(1− jTω ) |
|
|
||||||||
|
|
|
P(ω) = |
|
k |
; |
|
|
Q(ω) = − |
kTω |
; |
|||||
|
|
|
T2ω2 +1 |
|
|
T2ω2 +1 |
||||||||||
|
|
|
A(ω) = |
k |
|
; |
|
ϕ(ω) = −arctgTω; |
|
|||||||
|
|
|
T2ω2 +1 |
|
|
|||||||||||
График ЧХ в обычном масштабе (рис.35). |
|
|
|
|
|
|
|
|||||||||
Im(Q) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ω=∞ |
|
|
k/2 |
|
|
k |
|
Re(P) |
|
|
|
|
|
|
|
|
|
|
|
ϕ(ω1) |
A(ω1) |
ω=∞ |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
k/2 |
|
ω2 |
|
|
ω1 |
|
|
|
|
|
|
|
|
|
||
|
|
|
ωС =1/T |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
Рис.35 |
|
|
|
|
|
|
|
|
|
|
|||
3.3.2. ЛАХ: |
20lg A(ω) = 20lg |
k |
; |
|
|
|
|
|
|
|||||||
1+ T2ω2 |
|
|
|
|
|
|
||||||||||
При k = 1 20lg A(ω) = −20lg 1+ T2ω2 ;
1+ T2ω2 ;
Построение:
1.При малых частотах, где T2ω2 <<1, пренебрегаем T2ω2 = 0.
20lg A(ω) = −20lg1= 0.
2.При больших частотах, где T2ω2 >>1, пренебрегаем 1, тогда
20lg A(ω) = −20lgTω .
3. В области средних частот T2ω2 =1, отсюда определяем частоту сопряжения
1
низкочастотной и высокочастотной составляющей: ωC = T
25
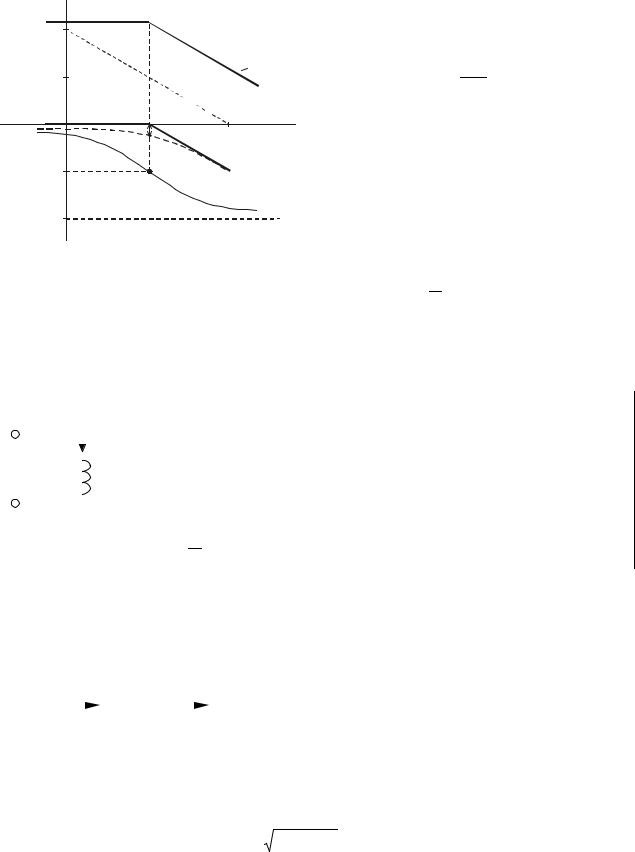
20lgA |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определим |
|
наклон |
высокочастотной |
||||||||
20lgk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
составляющей, для чего вычислим изменение |
||||||||||
20 |
вс |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
lg A при изменении частоты в 10 раз. |
|
|
||||||||||
|
п |
|
п |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
о |
|
|
м |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
д |
|
|
|
|
|
|
|
20lg∆A = −20lg10T + 20lgT = |
|
|
||||||||||
|
|
с |
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
т |
|
|
г |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
р |
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
оен |
|
ель |
|
|
|
|
|
|
|
|
|
|
/де |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
и |
|
|
|
н |
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
я |
- |
|
|
а |
|
|
|
|
|
|
|
|
|
|
., |
|
|
|
|
|
|
|
10T |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
я |
|
|
|
|
|
|
|
|
|
|
|
|
K |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
0дб |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ини |
|
|
|
|
|
|
|
|
|
=1 |
|
|
|
|
|
|
= −20lg10 = −20 дб |
|||||||||||
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
/ |
|
|
я |
д |
|
|
|
|
|
|
|
|
|
|
|
= −20lg T |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
де |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к. |
|
|
ля |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
1ω=∞ |
|
|
|
|
|
|
|
|
|
|
ωC |
|
|
|
|
|
|
|
|
|
|
10 |
|
ω |
т.е. при изменении частоты на одну декаду |
||||||||||||||
|
|
|
|
|
|
3 дб |
|
|
|
- |
|
|
|
|
|
|
(в 10 раз), ЛАХ |
уменьшается |
на |
20 |
дб, |
|||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
lgω |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20дб/ |
|
|
|
|
|
следовательно |
|
наклон |
|
высокочастотной |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
д |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
составляющей равен –20 дб/дек. |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
., |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
||
-45° |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ϕ |
|
|
|
|
|
|
|
|
1 |
|
Это |
мы |
построили |
приближенную |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
характеристику. |
|
Действительная |
|
АЧХ |
||||||
-90° |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
отличается в частоте сопряжения, как известно |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
из практики на 3 дб (что допустимо для |
|||||||||||
−ϕ |
|
|
|
|
|
|
Рис.36 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
инженерных расчетов) (рис.36). |
|
|
|
|||||||||||||||||||
ЛФХ (рис.36): ϕ(ω) = −arctgTω – тангенсойда, |
при ω = 0, ϕ = 0; |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
при ω =ω |
C |
= |
1 , |
ϕ = −45ο |
; |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
при ω = ∞, ϕ = −90ο. |
|
|
|
|
|
|||||
При k ≠ 1 ЛАХ перемещается параллельно самой себе по оси ординат на величину 20lgk , ЛФХ – |
||||||||||||||||||||||||||||||||||||||||
остается той же самой (рис.36). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
4.
|
|
R |
|
Uвх = iвых R + L |
diвых |
. |
|
|
|||
|
|
|
|
|
|
|
|
||||
|
|
|
|
iвых |
|
|
|
dt |
|
|
|
Uвх |
|
|
L |
Поделив на R, получим |
|
|
|||||
|
|
|
|
||||||||
|
|
T |
diвых |
+ iвых = kUвх , где k = |
1 |
, [1/Ом] – коэффициент передачи |
|||||
|
|
|
|
|
dt |
R |
|||||
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||
апериодического звена.
L
T = R , [сек.] постоянная времени апериодического звена.
4. Колебательное звено или звено 2-го порядка
1. Уравнение колебательного звена: |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
2 d2 x(t) |
|
|
|
dx(t) |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
g(t) |
|
x(t) |
|
|
T1 |
|
|
|
|
|
|
|
|
|
|
|
||
КЗ |
|
|
|
|
dt2 |
+ T2 |
|
dt + x(t) = kg(t), |
|
(1) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
причем T1 |
и T2 |
|
связаны между собой условием |
||||||||
|
|
|
рис. 37 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
T2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ξ = |
<1 |
|
(ξ – кси) |
|
(2) |
||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
2T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||
Условие (2) означает, |
что |
|
корни |
характеристического уравнения T2 |
λ2 |
+ T λ + 1= 0, |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
соответствующего дифференциального уравнения (1) являются комплексными |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
− T ± |
|
T2 − 4T2 |
|
|
|
|
(3) |
||||
|
|
|
|
λ1,2 |
= |
2 |
2 |
|
1 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
2T2 |
|
|
|
|
|
|
|
||||||
2. Переходя к преобразованию Лапласа |
1 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
(4) |
|||||||||
|
|
|
|
(T12 p2 |
+ T2 p+1)x(p) = kG(p) |
|
|
||||||||||||
получим передаточную функцию колебательного звена |
|
|
|
|
|
||||||||||||||
26
