6.3. Дисперсионный анализ результатов моделирования

При обработке и анализе результатов моделирования часто возникает задача сравнения средних выборок. Если в результате такой проверки окажется, что математическое ожидание совокупностей случайных переменных {y⁽¹⁾}, {y⁽²⁾}, …, {y⁽ⁿ⁾} отличается незначительно, то статистический материал, полученный в результате моделирования, можно считать однородным (в случае равенства двух первых моментов). Это дает возможность объединить все совокупности в одну и позволяет существенно увеличить информацию о свойствах исследуемой модели М_М, а следовательно, и системы S. Попарное использование для этих целей критериев Смирнова и Стьюдента для проверки нулевой гипотезы затруднено в связи с наличием большого числа выборок при моделировании системы. Поэтому для этой цели используется дисперсионный анализ.

Пример: Рассмотрим решение задачи дисперсионного анализа при обработке результатов моделирования системы в следующей постановке. Пусть генеральные совокупности случайной величины {у⁽¹⁾}, {y⁽²⁾}, ..., {y⁽ⁿ⁾} имеют нормальное распределение и одинаковую дисперсию. Необходимо по выборочным средним значениям при некотором уровне значимости γ проверять нулевую гипотезу H₀ о равенстве математических ожиданий. Выявим влияние на результаты моделирования только одного фактора, т.е. рассмотрим однофакторный дисперсионный анализ.

Допустим, изучаемый фактор x привел к выборке значений неслучайной величины Y следующего вида: y₁, y₂, ..., y_k, где k – количество уровней х. Влияние фактора будем оценивать неслучайной величиной D_x, называемой факторной дисперсией:

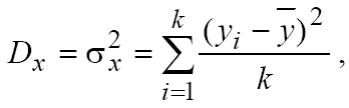
где y – среднее арифметическое значение величины Y.

Если генеральная дисперсия D[y] известна, то для оценки случайности разброса наблюдений необходимо сравнить D[y] с выборочной дисперсией S_в², используя критерий Фишера (F-распределение). Если эмпирическое значение F_э попадает в критическую область, то влияние фактора х считается значимым, а разброс значений х – неслучайным. Если генеральная дисперсия D[x] до проведения машинного эксперимента с моделью М_М неизвестна, то необходимо при моделировании найти ее оценку.

Пусть серия наблюдений на уровне y_i имеет вид: у_i1, у_i2, …, y_in,, где n – число повторных наблюдений на i-м уровне. Тогда на i-м уровне среднее значение наблюдений

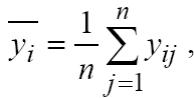
а среднее значение наблюдений по всем уровням

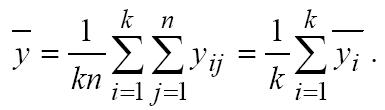
Общая выборочная дисперсия всех наблюдений

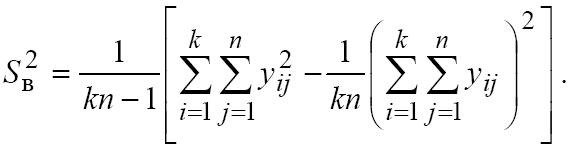
При этом разброс значений у определяется суммарным влиянием случайных причин и фактора х. Задача дисперсионного анализа состоит в том, чтобы разложить общую дисперсию D[у] на составляющие, связанные со случайными и неслучайными причинами.

Оценка генеральной дисперсии, связанной со случайными факторами,

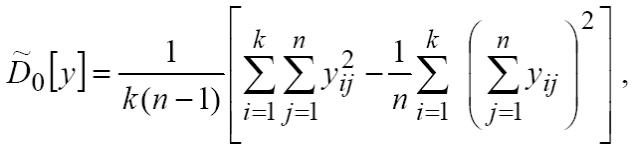
а оценка факторной дисперсии

.

Учитывая, что факторная дисперсия наиболее заметна при анализе средних значений на i-м уровне фактора, а остаточная дисперсия (дисперсия случайности) для средних значений в n раз меньше, чем для отдельных измерений, найдем точную оценку выборочной дисперсии:

.

Умножив обе части этого выражения на n, получим в правой части выборочную дисперсию S_в², имеющую (k–1)-ю степень свободы. Влияние фактора х будет значимым, если при заданном γ выполняется неравенство S_в²/D₀[y]>F_1-γ. В противном случае влиянием фактора х на результаты моделирования можно пренебречь и считать нулевую гипотезу Н₀ о равенстве средних значений на различных уровнях справедливой.

Таким образом, дисперсионный анализ позволяет вместо проверки нулевой гипотезы о равенстве средних значений выборок проводить при обработке результатов моделирования проверку нулевой гипотезы о тождественности выборочной и генеральной дисперсии.