Статья. Формирование у младших школьников общих умений решать текстовые задачи.

С 26 марта по 23 апреля 2008 года состоялся Первый интернет-марафон учебных предметов для учителей всей страны. Материалы читайте и смотрите на нашем сайте.

Работаю в школе более 20 лет и долгое время испытывала неудовлетворение, формируя у учащихся умение решать задачи. Наверное, это было связано с тем, что не все учащиеся могли самостоятельно справиться с решением задачи или же предлагали единственный способ решения.

Теперь, работая по учебнику математики Н.Б. Истоминой, поняла, что трудности, которые испытывали мои ученики при решении задач, были связаны с подходом, которого придерживалась, обучая их умению решать задачи. Хочу поделиться своими размышлениями.

В методической литературе принято рассматривать два основных подхода в формировании умения решать задачи. Первый – направлен на формирование умения решать задачи определённого вида, т.е. частное умение решать задачи; второй – на формирование общих способов действий при решении задач.

При первом подходе одновременно решаются две методические задачи, которые с точки зрения процесса обучения младших школьников математике противоречат друг другу. Противоречие заключается в том, что, с одной стороны, простую задачу используют как средство формир-я математического понятия, а с другой стороны, через эту же задачу организуется процесс формир-я умения решать з-чи.

Поэтому, чтобы преодолеть это противоречие методисты рекомендуют решать простые задачи на предметном уровне, практически (с помощью присчитывания). И, как правило, используются однообразные текстовые конструкции, которые всегда начинаются с условия, затем следует вопрос. Часто часть условия заменена рисунком. Это не способствует возникновению у младших школьников потребности анализировать текст задачи, т.е. представлять ситуацию, выявлять структурные компоненты задачи и устанавливать их взаимосвязь, формулировать текст задачи своими словами, моделировать условие задачи. Дети выделяют условие и вопрос, ориентируясь на внешние признаки. Далее даётся образец записи решения каждого типа задачи и на этапе закрепления решается большое количество аналогичных задач. Дети ориентируются на слова-действия: «было – осталось; прилетели – улетели» и т.д., или слова, указывающие на математические понятия: «увеличить на…», «уменьшить на…» и др. Поэтому суть всей работы сводится к «узнаванию» вида задачи.

Например, при решении задачи: «В гараже стояло 6 машин. 2 машины уехали. Сколько машин осталось в гараже?», ученики «рассуждают» так: «Это задача на нахождение остатка. Остаток нахожу вычитанием.» Или: «У Коли было 6 марок, а у Саши на 2 марки меньше. Сколько марок у Саши?» Дети ориентируются на слова: «на меньше..» и меньшее число находят вычитанием.

Как правило, простые задачи мои учащиеся решали хорошо, потому что систематически выносила простые задачи всех типов на контроль и наблюдала, как дети выбирают действия для решения задач. Если же какие-то задачи вызывали затруднения, то продолжала работать над «осознанием» понятия. Как мне казалось, осознание заключалось в распознавании слов, способствующих выбору действия. Долго не могла понять, почему же тогда при решении составных задач учащиеся испытывают затруднения? Казалось бы, научились решать простые задачи, входящие в составную, значит и с решением составной задачи дети должны справиться.

Самым трудным этапом работы над составной задачей был целенаправленный поиск решения. Использование разнообразных поисков пути решения задачи: аналитического, синтетического, аналитико-синтетического, не давало желаемых результатов, т. к. тот или иной путь привязан к способу решения, который наметил учитель. И учащиеся, в лучшем случае, запишут решение задачи одним способом, либо оставят задачу нерешённой, потому что забыли способ, который показал учитель, или не узнали вид задачи.

В учебнике математики Н.Б. Истоминой реализован другой подход в формировании умения решать задачи. Предложенный подход строится на утверждении необходимости формирования общих умений.

Н.Б. Истомина утверждает, что приступать к знакомству с текстовой задачей можно только после того, как у учащихся сформированы представления о смысле действия сложения и вычитания, их взаимосвязи, понятий «увеличить на…», «уменьшить на…», разностного сравнения. И я с ней абсолютно согласна, т. к. задача это новое для ребят математическое понятие, которое формировать без соответствующих базовых понятий невозможно.

Работая по учебнику Н.Б. Истоминой, я убедилась, что разнообразие методических приёмов, которые предлагает учебник, способствует формированию общих умений решать текстовые задачи, т. е. умению анализировать текст задачи, представлять его в виде схематической модели, умению осуществлять поиск пути решения, представлять текст в виде символической модели и проверять правильность решения.

Формулировки заданий способствуют активизации мыслительной деятельности учащихся и активному включению в конструктивный диалог.

Приведу примеры таких заданий из учебника для 2-го класса.

«Какую из этих задач ты можешь решить, а какую – нет? Почему?

а) Таня полила шесть грядок огурцов. Сколько грядок ей осталось полить?

б) На шахматной доске 20 фигур. Из них 13 чёрных, остальные – белые.

Сколько белых фигур на шахматной доске?»

Прочитав оба текста, уч-ся рассуждают так: «Первую задачу нельзя решить, т. к. не известно, сколько Тане надо полить грядок».

Одни предлагают свои варианты числовых данных. Например: «Тане надо полить 10 грядок огурцов. Она полила шесть грядок огурцов. Сколько грядок ей осталось полить?» Другие, выслушав одноклассников, тянут руки, чтобы ответить на поставленный вопрос, пользуясь понятием «целое» и «части», объясняют, как найти неизвестную часть: «10 – это целое, 6 - это часть, чтобы найти другую часть, надо от целого отнять известную часть».

«Вторую задачу можно решить, т. к. есть все необходимые данные».

Конечно, учитель видит детей, которые ещё не определились с выбором арифметического действия для решения задачи. Можно использовать приём выбора схемы. «Миша и Маша (герои учебника), - говорит учитель, - тоже для решения выбрали эту задачу и построили схемы:

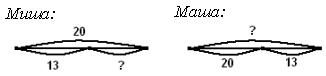
- Какая схема соответствует тексту задачи?

Если в классе находятся учащиеся, которые выбрали схему Маши, то я действую так: предлагаю им воспроизвести текст задачи, показывая на схеме, что обозначает каждое число. Один ученик читает текст задачи, другой демонстрирует на схеме, используя слова «целое и часть». Эти учащиеся убеждаются, что не обратили внимание в тексте на слова «из них»

Остаётся записать решение задачи в тетрадь. В зависимости от результатов самостоятельной работы учитель организует дальнейшую деятельность учащихся. Например: а) Дети записали решение задачи правильно 20 – 13 = 7 (ф.) В этом случае можно предложить проверить решение задачи, подставив полученные данные в схему. 20 – это 13 и 7; б) Если учитель увидел такие записи: 20 – 13 = 7 (ф.); 13 +7 = 20 (ф.); 20 – 7 = 13 (ф.), то можно вынести их на доску для обсуждения и использовать приёмы соотнесения рисунка и математической записи, выбор математической записи в соответствии с рисунком.

Учитель просит: «Покажите вопрос задачи на схеме. Это «целое» или «часть»? Как найти часть?» Дети убеждаются, что запись 13 + 7 = 20 – не соответствует сказанному. А равенство 20 – 7 = 13 – не соответствует схеме и тексту, т. к. 7 - нет на схеме и в условии. Это ответ. Две последних записи можно назвать проверкой решения.

Как видим, это задание способствует не только формированию умения анализировать текст задачи, осознанно выбирать арифметическое действие, но и совершенствованию вычислительных умений и навыков.

Ведущую роль в осознании текста, отношений, поиска пути решения и выбора арифметического действия играет схематическая модель. В процесс осознания отношений включаются понятия «целое» и «часть». Учебник постепенно формирует умение самостоятельно моделировать текст. Сначала предлагаются готовые модели с использованием приёма выбора схем, соответствующих или несоответствующих тексту задачи, затем – достраивание полуготовой модели до модели, соответствующей тексту задачи и, таким образом, к 3-му, 4-му классам учащимся предлагается самостоятельно построить схему.

Приведу пример задачи из учебника для 4 класса, где ни традиционная краткая запись, ни аналитический, синтетический или аналитико-синтетический способ разбора вряд ли помог бы учащимся в поиске пути решения: «На трёх полках стоит 45 книг, причём на одной в 2 раза меньше, чем на каждой из двух других. Сколько книг на каждой полке?»

После обсуждения процесса построения схемы, у учащихся появляется такая модель:

 

Рассмотрев схему, учащиеся замечают: «Целое число 45 состоит из 5-ти равных частей. Чтобы найти чему равна одна часть, надо 45 : 5 = 9. Теперь могу узнать, сколько книг на 2-й или на 3-ей полке. Надо 9 Х 2 = 18. Проверяю: 5 + 18 + 18 = 45 (кн.) – это соответствует условию».

Как показывает опыт, практически на каждом уроке учащиеся предлагают свои способы решения.

Например, при решении задачи из учебника 3 –го класса «Длина прямоугольника в 2 раза больше ширины. Чему равна площадь прямоугольника, если его периметр равен 30см? 15 дм? 6 см?»

Для работы с этой задачей на уроке выбрали одно из условий, а именно: «периметр прямоугольника равен 15 дм».

Один способ решения совпадает со способом решения, который подробно описан Н.Б. Истоминой в «Методических рекомендациях». Заостряю внимание на другой схеме и ином способе, который предложили учащиеся.

• 15 дм = 150 см

• 150 : 6 = 25 (см) – ширина

• 25 Х 2 = 50 (см) – длина

• 50 Х 25 = 1250 (кв. см) – площадь.

Значения второго и третьего действий учащиеся находили на калькуляторе.

В своей практике убедилась, что, формируя у младших школьников общие способы действия при решении тестовых задач, можно не только увеличить степень самостоятельности учащихся при моделировании ситуации задачи и отыскании ответа на вопрос, но и развить интерес к поиску наиболее рациональных способов решения.