8.1.Общие вопросы методики обучения алгоритмам письменных вычислений.Формирование письм.Вычислительных навыков учащихся.

При сложении многозначных чисел в основе действий учащихся лежит алгоритм сложения, суть которого сводится к следующему:

1. Записывают второе слагаемое под первым так, чтобы соответствующие разряды находились друг под другом.

2. Складывают цифры (этот термин используется для краткости, вообще здесь речь идет об однозначном числе, обозначаемом цифрой) разряда единиц. Если сумма меньше 10, ее записывают в разряд единиц ответа и переходят к следующему разряду.

3. Если сумма цифр единиц больше или равна 10, то представляют ее в виде: 10 + С₀, где С₀ — однозначное число; записывают С₀ в разряд единиц ответа и прибавляют 1 к цифре десятков первого слагаемого, после чего переходят к разряду десятков.

4. Повторяют те же действия с десятками, потом с сотнями и т. д. Процесс сложения заканчивается, когда произведено сложение цифр старших разрядов.

Алгоритм вычитания многозначных чисел можно представить в таком виде:

1. Записывают вычитаемое b_n b_{n – 1} … b₁ b₀ под уменьшаемым

a_n а_{n - 1} ... а₁ а₀ так, чтобы соответствующие разряды находились друг под другом.

2. Если цифра в разряде единиц вычитаемого не превосходит соответствующей цифры уменьшаемого, то ее вычитают из соответствующей цифры уменьшаемого, после чего переходят к следующему разряду.

З. Если цифра единиц вычитаемого больше цифры единиц уменьшаемого, т. е. а₀ < b₀, а цифра десятков уменьшаемого отлична от нуля, то уменьшают цифру десятков уменьшаемого на 1, одновременно увеличивают цифру единиц уменьшаемого на 10, после чего вычитают из числа 10 + а₀ число b₀ и записывают результат в разряде единиц разности. далее переходят к следующему разряду.

4. Если цифра единиц вычитаемого больше цифры единиц уменьшаемого, а цифры, стоящие в разряде десятков, сотен и т. д. уменьшаемого, равны нулю, то берут первую, отличную от нуля, цифру в уменьшаемом (после разряда единиц), уменьшают ее на 1, все цифры в младших разрядах до разряда десятков включительно увеличивают на 9, а цифру в разряде единиц — на 10, вычитают b₀ из 10 + а₀, записывают результат в разряде единиц разности и переходят к следующему разряду.

5. В следующем разряде описанный процесс повторяется.

6. Процесс вычитания заканчивается, когда произведено вычитание из старшего разряда уменьшаемого.

Безусловно, младшие школьники не могут усвоить алгоритмы письменного сложения и вычитания в общем виде. Но учителю знать их необходимо. Это позволит ему:

а) при ознакомлении учащихся с алгоритмом правильно организовать подготовительную работу;

б) управлять деятельностью школьников, направленной на усвоение алгоритма;

в) в упражнениях на закрепление алгоритма учитывать все возможности его использования.

Приведенные выше описания алгоритмов даются учащимся нач.кл. в упрощенном виде, где фиксируются только осн.моменты:

1) второе слаг-е (вычит-е) нужно записать под первым (под уменьшаемым) так, чтобы соотв-е разряды находились друг под другом;

2) сложение (вычитание) следует начинать с низшего разряда, т.е. складывать (вычитать) сначала единицы.

Другие операции, входящие в алгоритмы, либо разъясняются младшим школьникам на конкретных примерах, либо осознаются ими в процессе выполнения специально подобранных упражнений.

Деятельность учащихся, направленная на формирование навыков письменного сложения и вычитания, может быть организована по-разному.

Например, в учебнике М2М (издания до 1987 г.) учащиеся знакомились с приемами письменного сложения и вычитания в концентре «Тысяча». А в учебнике М2М (издания после 1987 г.) им показывали, как складывать и вычитать «В столбик» уже двузначные числа. для этой цели использовался образец действий.

Объясни решение примера:

49 + 23 = 49 + (20 + 3) = 69 + 3 = 72

Решение можно записать «В столбик»:

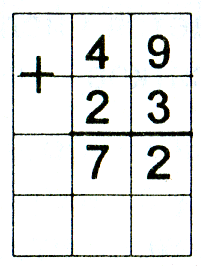
Объяснение:

1. Пишу...

2. Складываю единицы: 9 + 3 = 12. 12 — это 1 дес. и 2 ед.; пишу под единицами 2, а 1 дес. запоминаю и прибавляю к десяткам.

3. Складываю десятки: 4 + 2 = 6; 6 да еще 1, получится 7. Пишу 7 под десятками.

4. Читаю ответ: сумма равна 72.

Аналогичный комментарий дан к записи вычитания «В столбик». Введение письменного сложения и вычитания двузначных чисел было по-разному воспринято учителями. Одни считали, что выполнение действий «В столбик» окажет негативное влияние на формирование навыков устных вычислений, другие отнеслись к этому положительно, так как при устном сложении и вычитании двузначных чисел с переходом через разряд учащимся приходится пользоваться приемами вычислений, содержащих большое количество операций. Это требует напряжения памяти и внимания, из-за чего не все дети могут справиться с вычислительной задачей.

В случае же письмен. сложения алгоритмическое предписание им. более четкую и краткую форму, а значит, более доступную детям.

Вряд ли можно согласиться с точкой зрения тех учителей, которые считают, что запись сложения и вычитания в столбик» оказывает негативное влияние на формирование вычислительных навыков, так как при выполнении письменных вычислений учащиеся Постоянно используют навыки сложения (вычитания) в пределах 10 и 20.

Поэтому проблема не в том, когда познакомить школьников с алгоритмом письменного сложения и вычитания, а в том, как продуктивнее организовать их деятельность, направленную на усвоение алгоритма.

В учебнике М2М в концентре «Тысяча» внимание учащихся акцентируется на каждом частном случае сложения и вычитания. Сначала ребята упражняются в сложении и вычитании чисел без перехода через разряд:

Затем рассматриваются случаи, когда при сложении разрядных единиц получается число, равное 10 единицам, или при сложении разрядных десятков — число, равное 10 десяткам:

Затем случай, когда при сложении разрядных десятков получается число, большее 10 десятков:

Затем случай, когда при сложении разрядных единиц получается число, большее 10 единиц, и при сложении десятков — большее 10 десятков:

Так же последовательно рассматриваются различные случаи вычитания трехзначных чисел:

Для каждого случая дается образец действия, которое затем закрепляется в процессе выполнения аналогичных упражнений.

Так как предполагается, что алгоритмом письменного сложения и вычитания учащиеся овладели в концентре «Тысяча», то тема «Сложение и вычитание многозначных чисел» в учебнике М3М начинается с установки: «Письменное сложение и вычитание многозначных чисел выполняется так же, как сложение и вычитание трехзначных чисел».

Рассмотрим другой подход к изучению алгоритмов письменного сложения и вычитания, который нашел отражение в учебнике М2И.

В отличие от рассмотренного подхода дети знакомятся с алгоритмами письменного сложения и вычитания только после того, как они усвоят нумерацию чисел в пределах миллиона. При этом их деятельность направлена не на отработку частных случаев сложения и вычитания, а на осознание тех операций, которые входят в алгоритмы. Для этого уже при изучении нумерации их внимание обращается на то, как изменяется цифра, стоящая в определенном разряде данного числа при его увеличении (уменьшении) на разрядные единицы, десятки, сотни, тысячи и т. д.

В процессе этих упражнений дети осознают соотношение разрядов, их «переполнение» и значение каждой цифры в записи числа. Это способствует сознательному усвоению механизма письменного сложения и вычитания.

Приступая к изучению алгоритмов письменного сложения и вычитания, учащиеся выполняют задание:

На сколько можно увеличить 308287, чтобы изменились цифры, Стоящие в разряде единиц и десятков, а цифры в других разрядах остались те. Маша записала свой ответ так:

Миша так:

На сколько увеличила число Маша? На сколько — Миша? Как они рассуждали? Возможны ли другие варианты ответа на поставленный вопрос?

Последний вопрос позволяет проанализировать все возможные варианты и сделать обобщение: если получаем в соответствующем разряде 10 единиц или больше 10 единиц, то изменяется цифра следующего высшего разряда.

Второе задание связано с анализом способа действия при сложении «в столбик». При этом приведенные образцы включают различные случаи.

Объясни, как выполнено сложение чисел. Догадайся: почему сложение многозначных чисел «в столбик» нужно начинать с разряда единиц?

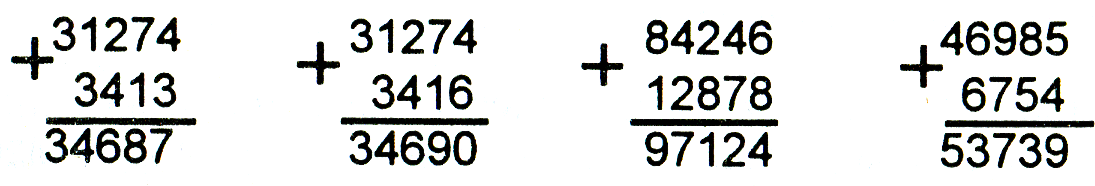
Затем внимание детей акцентируется на выполнении записи «в столбик». Для этой цели обсуждаются две записи, одна из которых верная, а другая — неверная.

Вычисли значение суммы: 3502+121346.

Маша выполнила задание так:

Миша — так:

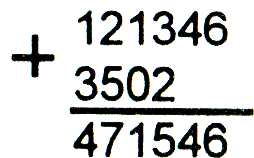
Догадайся! Кто допустил ошибку и в чем ее причина? Проверь свое предположение с помощью калькулятора.

Такой же методический подход используется при формировании у учащихся умения выполнять вычитание чисел «в столбик».

Усвоение младшими школьниками нумерации трехзначных и многозначных чисел позволяет им осуществить перенос умения складывать и вычитать двузначные числа «столбиком» на область трехзначных и многозначных чисел.

Задание 72. Найдите в учебниках М2 (1-111) и МЗ (1-1V) страницы, на которых даются разъяснения алгоритма письменного сложения и вычитания трехзначных и многозначных чисел. При каких условиях ученики смогут самостоятельно выполнять письменное сложение и вычитание трехзначных и многозначных чисел, воспользовавшись этими разъяснениями.

Следует иметь в виду, что письменное сложение и вычитание многозначных чисел требует от детей предельного внимания и аккуратной записи. Практика показывает, что если ученик решает, например, сразу более 4—5 примеров на сложение и вычитание многозначных чисел, то количество допускаемых им ошибок возрастает. Это связано с тем напряжением внимания, которое необходимо для выполнения операций, входящих в состав алгоритмов. Поэтому необходимо соблюдение количественной меры решаемых ими примеров и вариативности тех заданий, которые связаны с выполнением письменных вычислений.

Для этого помимо таких заданий, как «вычисли, записывая примеры столбиком»: 259+325, 48+821, 348+524», можно использовать следующие виды заданий:

а) найди ошибку в вычислениях:

375 489

854

б) объясни решение примеров 437

95

532

в) какие цифры пропущены

7. . .02 660

326

807

Задание 73. Найдите в учебниках МЗ и М4 (1-1У) страницы, связанные с изучением сложения и вычитания величин. Объясните, почему сложение и вычитание величин можно применять для закрепления приемов устного и письменного сложения и вычитания чисел.

АЛГОРИТМ ПИСЬМЕННОГО УМНОЖЕНИЯ

Из курса математики вам известно, что письменное умножение опирается на:

• запись чисел в десятичной системе счисления,

• таблицу умножения однозначных чисел,

• законы сложения и умножения,

• таблицу сложения однозначных чисел.

Поэтому младшие школьники знакомятся с алгоритмом письменного умножения после изучения всех названных понятий. Применяя знание разрядного состава числа и свойство умножения суммы на число, они могут умножить любое многозначное число на однозначное, выполнив устные вычисления, но большинство из них легко справляются с этой задачей только в том случае, если нет перехода через разряд: 324x2, 1233x3, 4232x2 и т.д. При выполнении вычислений для случая с переходом через разряд возникает необходимость фиксировать промежуточные результаты в том или ином виде:

а) 426x3= (400+20+6) хЗ=400хЗ+20хЗ+6хЗ=1200+60+18=1278;

б) 426x3=1200+60+18=1278.

Для более сложных случаев сложение промежуточных результатов необходимо выполнять в столбик: 9347x8=9000x8+300x8+40x8+7x8

7200 2400

320

56

Это затрудняет вычислительную задачу, поэтому возникает необходимость познакомить детей с алгоритмом письменного умножения или с умножением «в столбик».

Объясняя школьникам письменное умножение, полезно учитывать, что с выполнением действий «в столбик» они уже познакомились, складывая и вычитая многозначные числа. Поэтому необходимо обратить их внимание на то, что принцип записи чисел «в столбик» при умножении остается таким же, как при сложении: второе число подписывается под первым таким образом, чтобы его разряды были под соответствующими разрядами первого числа:

375 3

375 284

375 31

Практика показывает, что дети с трудом понимают ту взаимосвязь, которая существует между устными и письменными вычислениями и соотнести между собой запись «в строчку» и «в столбик». Поэтому при объяснении алгоритма письменного умножения важно выделить для ребенка основные ориентиры его действий: 1) умножение, так же как и сложение, начинаем с единиц низшего разряда (первого разряда); 2) записывая полученный результат, следим за тем, чтобы каждый разряд числа, полученного в произведении был под соответствующим ему разрядом. Объясняя детям алгоритм письменного умножения на конкретном примере, на эти моменты следует обращать особое внимание. Приступая, например, к умножению чисел 426x3, учитель прежде всего выясняет: Как выполнить эту запись в столбик? (Второй множитель содержит три единицы, значит цифру три нужно записать под разрядом единиц первого множителя:

426 3

Далее следует обратить их внимание на то, что умножение начинаем с единиц: 6x3=18, 18 это 1 дес. и 8 ед. Следуя второму ориентиру в разряде единиц можно записать только цифру, обозначающую единицы, 1 дес. нужно запомнить.

Ученики легко справляются с этими операциями, так как они уже выполняли их при сложении чисел в столбик. Действуя по аналогии с алгоритмом письменного сложения, некоторые из них сразу прибавляют 1 дес. к 2 дес. первого множителя и после этого выполняют умножение на 3. Для предупреждения подобной ошибки полезно обратить внимание на то действие, которое они выполняют. Так как выполняется умножение, то сначала надо умножить десятки на число, потом прибавить тот десяток, который запомнили, т.е. 2 дес.хЗ=6 дес. В разряде десятков записывается цифра 6. После этого умножаем сотни: 4 сот.хЗ=12 сот. (12 сот. — это 1 тыс. и 2 сот. В разряде сотен записываем цифру 2, в разряде тысяч — цифру 1.)

Следует также отметить, что появление такой ошибки зависит от той последовательности операций, которая имела место при сложении чисел «в столбик». Некоторые учителя при сложении «в столбик» рекомендуют детям сразу прибавить ту разрядную единицу, которую запомнили к соответствующей разрядной единице первого слагаемого, затем уже к полученному результату прибавлять единицы соответствующего разряда второго слагаемого. Обосновывается такая последовательность операций тем, что они могут забыть то число, которое запоминали, поэтому лучше его прибавить сразу. Это не совсем верно. Лучше сориентировать их на такую последовательность операций: сначала складываем разрядные единицы первого и второго слагаемого, затем прибавляем то число, которое запомнили. Это поможет уменьшить количество ошибок при умножении «в столбик».

После объяснения алгоритма умножения на однозначное число не следует сразу приступать к решению примеров, отрабатывая различные частные случаи умножения на однозначное число, т.е. умножение трехзначного числа на однозначное, четырехзначного числа на однозначное, случай когда в первом множителе отсутствуют разрядные единицы (408x7, 40016x5). Гораздо важнее, чтобы дети осознанно усвоили последовательность операций, входящих в алгоритм. Для этой цели полезно выполнять с ними такие задания:

1. Прокомментировать решенные примеры:

284 615

3_ 4_

852 2460

2. Вставить в «окошки» пропущенные цифры, чтобы запись была вер-

ной:

428 6

62517 4

25. 8

25 . О . 8

3. Соотнести записанные произведения с данными ответами. Учитель выписывает слева четыре произведения, справа четыре числа, которые являются ответами данных примеров. Нужно догадаться, какой ответ будет в каждом примере, не выполняя вычислений «в столбик»:

615x3 2568

924x5 5544

924x6 4620

428x6 1845

Так как умножение начинается с единиц низшего разряда, то для выполнения этого задания достаточно проверить последнюю цифру, т.е. выполнить умножение единиц (табличное умножение).

При составлении таких заданий необходимо соответствующим образом подобрать выражения (в результате не должно получаться чисел, оканчивающихся одинаковой цифрой).

4. Найти ошибку в вычислениях. Причина ошибки может быть связана с незнанием таблицы умножения или ученик забыл прибавить число, которое запоминал:

5006

7_

35772

5006

5006

7_

35002

35812

В первом случае он ошибся при умножении нуля на число 7, во втором — забыл прибавить 4 дес., в третьем — ошибка связана с умножением нуля на число.

5. Выполнить прикидку результата. Младшим школьникам предлагается догадаться, сколько цифр получится в произведении, не выполняя умножения. Они ориентируются на разрядный состав числа: «6088x4. 6 тыс. умножаем на 4, получаем 24 тыс., значит в ответе — пятизначное число». Предположение проверяется умножением в «столбик».

Задание 74. Найдите в учебниках МЗ (1-1У) и МЗ (1-111) страницы, на которых дети знакомятся с алгоритмом письменного умножения. Сравните объяснения на этих страницах. В чем их сходство и различие? Как бы вы познакомили учащихся с алгоритмом письменного умножения на однозначное число? Придумайте упражнения на закрепление алгоритма письменного умножения.

При изучении алгоритма письменного умножения на однозначное число необходимо специально уделить внимание записи «в столбик» для случая умножения числа, оканчивающегося нулями:

720 3700

6 6

Важно, чтобы дети понимали, что способ записи, с которым они познакомились на первом уроке изучения алгоритма правомерен и для случая умножения чисел, оканчивающихся нулями:

720 3700

6 6

Но для того, чтобы не выполнять лишних операций, кот.связаны с умножением нуля на число, принято использ. такую запись:

720 3800

4 5

Она позволяет нули, стоящие на конце первого множителя, перенести в ответ. Для осознания этого факта можно предложить упражнения вида:

130x5 2300x4

13 дес.х5=65 дес. 23 сот.х4=92 сот.

Знание переместительного свойства умножения позволяет учащимся применять алгоритм умножения на однозначное число и для нахождения произведения, в котором первый множитель однозначное число, второй – многозначное. Для этого нужно только переставить множители и воспользоваться для вычисления результата алгоритмом умножения на однозначное число. Знание сочетательного свойства умножения позволяет им пользоваться алгоритмом письменного умножения и в том случае, когда второй множитель можно представить в виде произведения однозначного числа и числа, записанного единицей с нулями:

375х50=375х(5хЮ)=(375х5)х10

375х500=375х(5хЮО)=(375х5)х100

375х5000=375х (5х 1000)=(375x5) х 1000

Для письменных вычислений в этих случаях используется запись:

375 375 375

5 500 5000

С алгоритмом умножения на однозначное число связано также вычисление произведения, в котором первый множитель — любое число, оканчивающееся нулями, второй множитель — число, которое можно представить в виде произведения однозначного числа и числа, записанного единицей с нулями.

375000 700

Задание 75. Найдите в учебниках МЗ (1-П1) и М4 (1-1У) страницы с заданиями, при выполнении которых дети могут воспользоваться алгоритмом умножения на однозначное число. Как вы объясните им образцы записей, приведенных на этих страницах?

Алгоритм письменного умножения на однозначное число — основа овладения учащимися алгоритмом письменного умножения на двузначное и трехзначное числа. Поэтому при разъяснении алгоритма умножения на двузначное и трехзначное числа необходимо показать их взаимосвязь. Для этой цели второй множитель можно представить в виде суммы разрядных слагаемых:

62х47=62х(40+7)=62х40+62х7.

Пользуясь алгоритмом умножения на однозначное число, ученики вычисляют первое и второе произведения, затем складывают полученные результаты. После этого учителю нужно только показать более компактную запись выполненных операций:

47 434 248 2914

Комментируя действия, связанные с выполнением этой записи, целесообразно ввести понятия: первое неполное произведение (оно получается при умножении данного числа на число, обозначенное цифрой, стоящей в разряде единиц второго множителя), второе неполное произведение (оно получается при умножении данного числа на число, обозначенное цифрой, стоящей в разряде десятков второго множителя).

Для осознанного усвоения операций, входящих в алгоритм умножения на двузначное число, полезно предложить детям сравнить и проанализировать следующие записи:

62 62 62

47 47 47

434 434 434

2480 248 248

2914 2914

В результате такого анализа делается вывод о том, какая запись неверная, какая — верная, и какой из верных записей удобнее пользоваться. Алгоритм умножения на трехзначное число целесообразно рассматривать в сравнении с алгоритмом умножения на двузначное число.

Задание 76. Найдите в учебниках МЗ (1-П1) и М4 (1-1V) различные виды упражнений на закрепление тех операций, которые входят в алгоритмы письменного умножения на двузначное и трехзначное числа. Придумайте упражнения, которые вы могли бы предложить учащимся с этой же целью.

АЛГОРИТМ ПИСЬМЕННОГО ДЕЛЕНИЯ

Из курса математики вам известно, что письменное деление рассматривается как действие деления с остатком. Поэтому сознательное овладение алгоритмом письменного деления во многом зависит от умения находить остаток при делении одного числа на другое. Основа этого умения — осознание взаимосвязи между делимым, делителем, неполным частным и остатком, которая находит выражение в равенствах: а=Ьд+г, г=а-Ья, ^ГДС а — делимое, Ь — делитель, ^ — неполное частное, г — остаток.

Как было ранее сказано (см.п. «Деление с остатком»), эта связь лучше осознается детьми в том случае, когда они выполняют деление с остатком, используя способ подбора, позволяющий сконцентрировать их внимание на взаимосвязи умножения и деления, на способе нахождения остатка и на том, что остаток должен быть меньше делителя.

Следует отметить, что по действующей программе до знакомства с алгоритмом письменного деления ученики решают на деление с остатком только примеры, которые связаны с табличными случаями деления. В связи с этим, выполняя вычисления, они чаще используют знание таблицы деления, чем способ подбора. Например, решение примера 29:7 они начинают с утверждения — 29 на 7 не делится, самое большое число, меньшее, чем 29, которое делится на 7 — это 28, разделим 28 на 4, получим 7 и 1 в остатке. Операция нахождения остатка фактически осуществляется в свернутом виде, как 29—28 (это легко сделать по отношению к табличным случаям, усвоение которых доведено до автоматизма, но тогда из поля зрения учащихся выпадает та связь, которая существует между числами 28, 7, 4 и остатком 1).

Это отрицательно сказывается как на усвоении последовательности операций, входящих в алгоритм письменного деления, так и на оформлении записи «уголком». Например, выполняя деление 872 3, дети рассуждают следующим образом: «8 разделим на 3, получится 2 и 2 в остатке». Но так как форма записи здесь иная, чем 8:3=2 (ост. 2), то многие из них не могут понять, где нужно записать частное 2, а где остаток 2, а также не могут объяснить сам способ нахождения остатка, т.е. 8—3x2=2.

Для предупреждения этих трудностей некоторые методисты предлагают познакомить детей с записью «уголком» уже при изучении темы «Деление с остатком»:

29

28 1

Другие предлагают сделать это непосредственно перед знакомством с

• алгоритмом письменного деления, используя приведенные выше примеры.

Это, конечно, помогает овладеть формой записи письменного деления, но не сосредотачивает их внимания на способе нахождения остатка. Для этой цели полезно предлагать детям решать примеры с остатком для случаев деления двузначного числа на двузначное. Например, 52:17. Ученики будут рассуждать так: пробуем число 2: 17x2=34, 52—34=18, 18>17, но остаток не может быть больше делителя. Пробуем число 3: 17x3=51, 52—51=1, К17. Получим 52:17=3 (ост.1).

Для осознания операций, связанных с нахождением остатка, полезны также упражнения вида: «Вставь числа в «окошки», чтобы получилась верная запись:

29:7=4 (ост.Ц )

29: Ц=4 (ост.5)

29:6=0] (ост. ^])

Помимо деления с остатком, как одной из основных операций алгоритма письменного деления, для успешного овладения алгоритмом ученики должны усвоить разрядный состав числа и соотношение разрядных единиц.

Эти знания также используются при выполнении операций, входящих в алгоритм письменного деления.

Задание 77. Найдите в учебниках МЗ (1-Ш) и М4 (1-1V) страницы, на которых дети знакомятся с алгоритмом письменного деления. Сравните их между собой. В чем их сходство и различие? Какие случаи деления рассматриваются в учебниках при знакомстве с алгоритмом деления? Попытайтесь изложить последовательность тех операций, которые вы будете выполнять, объясняя детям алгоритм письменного деления.

Формирование у младших школьников навыков письменного деления зависит не только от усвоения ими математических понятий и способов действий, лежащих в основе алгоритма, но и от того как будет построен сам процесс усвоения алгоритма.

В учебниках математики для начальных классов находит отражение подход, при котором дети овладевают алгоритмом письменного деления, последовательно рассматривая различные частные случаи деления чисел. Например, при делении на однозначное число сначала рассматривается случай, когда первое неполное делимое выражается однозначным числом, обозначающим количество сотен: 794:2, 984:4, 985:5, 681:3, затем отрабатывается умение делить числа для случая, когда первое неполное делимое — двузначное число, обозначающее количество десятков: 376:4, 1984:8.

Затем отрабатывается умение делить числа для случаев, когда в частном получается нуль на конце или в середине: 4680:3, 432:4. После этого — случай деления с остатком, затем — случай деления чисел, оканчивающихся нулями: 5130:90, 2580:30, 46800:600, 37600:400.

Отдельно отрабатывается умение делить на двузначные и трехзначные числа. Описанный подход не позволяет учащимся сосредоточить внимание на том общем способе действий, которым они могут пользоваться практически для каждого рассмотренного случая. Это сковывает их самостоятельность при выполнении письменного деления и отрицательно сказывается не только на активизации мыслительной деятельности, которая связана с осознанием операций, входящих в алгоритм, но и на формировании навыков письменного деления.

Практика показывает, что более эффективным является подход, при котором ученики применяют общий способ действия для решения различных примеров, устанавливая сходство и различие выполненных действий. Например, одновременное решение примеров 672:2 и 672:8 позволит им лучше осознать такую операцию, как выделение первого неполного делимого и определения количества цифр в частном.

Случаи 792:2 и 432:4 также полезно рассмотреть в сравнении, проследив образование второго неполного делимого в одном и другом примере.

Задание 78. Сравните приведенное ниже объяснение алгоритма письменного деления с теми, которые даны в учебниках МЗ (1-111) и М4 (1-1У). В чем вы видите их отличия?

1. Выделяем первое неполное делимое (самое маленькое число, которое можно делить на делитель) 792 2. Это 7 сот.

2. Определяем количество цифр в частном (делим сотни, значит первая цифра в частном обозначает сотни. Если в числе есть разряд сотен, то значит есть разряд десятков и единиц). В частном получаем три цифры:

792 I 2

3. Подбираем первую цифру частного (цифра 3):

792 | 2

I 3.. ;

4. Находим остаток. Для этого 3x2=6, 7—6=1, остаток равен 1: 3..

792 6

5. Выделяем второе неполное делимое. Оно состоит из остатка и единиц следующего разряда:

792

6

19

6. Выполняем операции 3, 4 со вторым неполным делимым, т.е. подбираем вторую цифру в частном и находим остаток:

792 2 6 | 39. 19 18

7. Образуем неполное делимое из остатка и единиц низшего разряда: 39.

792 6 19 18 12

8. Повторяем операции 3, 4 для третьего неполного делимого:

Задание 79. Прокомментируйте свои действия при решении следующих примеров: 3456728:7; 54673897:27.

При решении примеров, в которых делимое и делитель оканчиваются нулями, можно воспользоваться свойством деления числа на произведение или с приемом вычислений, в основе которого знание десятичного состава числа.

Например, для нахождения значения частного: 40160:80 учащиеся могут представить делитель в виде произведения двух множителей: 40160: (8x10). Воспользовавшись свойством деления числа на произведение, получим: (40160:10):8. Таким образом, решение данного примера сведется к случаю: 4016:8, т.е. к применению алгоритма деления на однозначное число.

Можно при решении данного примера сначала выделить кол-во десятков в делимом и делителе (40160=4016 дес.; 80=8 дес.), после этого вып-ть деление на однозн.число, смысл которого будет сводиться к ответу на вопрос: «Во сколько раз 4016 дес. больше, чем 8 дес.?».

При делении на двузначное и трехзначное числа учащиеся фактически пользуются алгоритмом деления на однозначное число, но сам механизм вычислений для этих случаев деления оказывается для них несколько сложнее. Он требует не только усвоения операций, входящих в алгоритм и прочных знаний табличных случаев умножения и деления, но и овладения способом прикидки результата. Например, при нахождении значения частного: 4316:52, они сначала выделяют первое неполное делимое 431. Так как это число обозначает количество десятков, то высшим рязрядом частного будут десятки, т.е. частное будет записано двумя цифрами.

Подбор цифры, обозначающей десятки в частном, фактически сводится к выполнению деления с остатком: (431:52). Для этого подбора можно выделить число десятков в числе 431 (43 дес.) и в числе 52 (5 дес.) и разделить 43 дес. на 5 дес. В этом случае при подборе цифры в частном можно использовать знание таблицы умножения. Предположив, что первая цифра в частном 8, проверяем ее (8x52=416). Находим остаток (431—416=15). Он меньше делителя, значит первая цифра в частном найдена верно. Аналогичные рассуждения проводятся со вторым неполным делимым (156:52). Запись приведенных рассуждений при письменном делении на двузначное число может выглядеть так:

52 4316 I 52

8 416 83

416 156

156 О

Так как при делении на трехзначное число первое неполное делимое может быть только трехзначным или четырёхзначным числом, то для подбора цифры в частном целесообразно выделять в неполном делимом и делителе количество сотен.

Например:

7552 I 236 708 | 32

472

472 О

Первое неполное делимое 755. Делим 755 на 236. Подбираем цифру в частном. Для этого 7 сот. делим на 2 сот., получаем 3. Проверяем ее (236x3=472). Находим остаток. Он меньше делителя (47<236). Сносим цифру 2. Делим второе неполное делимое 472 на 236.

Рассуждаем также: 4 сот. разделить на 2 сот. — получим 2. Проверяем цифру частного 236x2=472. Остаток равен нулю. Деление закончено.

Задание 80. Найдите значение частного: 4256:532, 7595:217, 2002:143, 9300:372, используя алгоритм письменного деления и приведите возможные рассуждения детей при выполнении вычислений. При формировании навыков письменного деления полезно предлагать им упражнения не только на вычисление результата, но и задания, при выполнении которых они отрабатывают операции, входящие в состав алгоритма письменного деления. Например:

1. Не производя вычислений, определите, сколько цифр получится в частном: 11475:27, 4378:48, 845386:32.

2. Какие цифры должны стоять вместо звездочек?

3. Найдите и исправьте ошибки, допущенные в вычислениях.

4. Не вычисляя, выберите правильный ответ: 8, 32, 9, 15:

3945:263 6201:689 18144:567 7472:934

При выполнении задания младшие школьники ориентируются на количество цифр в частном и на результат умножения чисел, записанных цифрами, стоящими в разряде единиц делимого и частного. Например, при делении 3945:263 получается в частном две цифры. Какое из чисел — 32 или 15 — получится в ответе? Для проверки достаточно умножить единицы частного на единицы делителя. Должны получить ед-цы делимого (2x3=6). Этот ответ не подходит, так как последняя цифра делимого 5. Аналогично проверяем ответ 15.

5. Составьте такой пример на деление, чтобы в частном получилось число 308, а делитель был бы любым двузначным числом. Для составления такого примера учащиеся умножают 308 на любое двузначное число, например: 308x24=7392.

Пример на деление 7992:24 можно решить затем «уголком».