§7. Закони збереження для електромагнітних явищ.

Закони збереження енергії, імпульсу, моменту імпульсу й електричного заряду є фундаментальними законами фізики. Із сучасної теоретичної точки зору ці закони збереження вважаються наслідком різних симетрій фізичного світу: збереження енергії, імпульсу і моменту імпульсу – наслідок симетрії простору і часу (однорідності часу, однорідності і ізотропності простору); збереження електричного заряду є наслідок так званої каліброваної симетрії. (см. §6) рівнянь теорії поля (ця симетрія зв'язана не з властивостями простору-часу, а з внутрішніми властивостями самих фізичних полів; послідовний розгляд каліброваної симетрії можливо тільки в квантовій теорії поля). Ці точні закони збереження (і симетрії, що лежать у їхній основі) є більш загальними законами (принципами) фізики в порівнянні з конкретними рівняннями руху в різних фізичних теоріях. Тому всі інші закони фізики повинні узгоджуватися з законами збереження. Зокрема, з перерахованими вище законами збереження узгоджуються і рівняння термодинаміки. Іншими словами, із рівнянь Максвела повинні випливати закони збереження електричного заряду, енергії, імпульсу і моменту імпульсу для електромагнітних систем (тобто довільних систем електричних зарядів, що рухаються, разом з електромагнітними полями).

Почнемо з закону збереження електричного заряду. Рівняння Максвела (5.1) і (5.3), у котрі входить електричний заряд (у вигляді густини заряду і густини струму ), повинні бути сумісні з цим законом. Для перевірки цього застосуємо операції дивергенції до лівої і правої частин рівняння (5.1). Так як в силу тотожності divrot = 0, то ми при цьому одержимо:

Змінюючи місцями операції div і в другому доданку, а потім позбавляючись від функції div за допомогою рівняння (5.3), одержуємо

(7.1)

Рівняння (7.1) називається рівнянням безперервності і є законом збереження електричного заряду в диференціальній формі. Щоб переконатися в цьому, перетворимо (7.1) до інтегрального виду, проінтегрувавши його по довільному (але фіксованому) об'єму V:

Переходячи в правій частині до інтегрування по поверхні за допомогою математичної теореми Гауса-Остроградского (2.19), а також змінюючи місцями операції й у лівій частині, одержуємо:

(7.2)

де S - замкнута поверхня, що охоплює виділений об'єм V. Відзначимо, що в лівій частині (7,2) замість частинної похідної за часом ми пишемо повну похідну в силу фіксованості об'єму V (тобто область інтегрування від часу не залежить).

У співвідношенні (7.2) ліворуч стоїть зміна заряду в об'ємі V за одиницю часу, праворуч - кількість зарядів, що входять через поверхню S за одиницю часу. Рівність (7.2) цих двох величин і є закон збереження заряду. Знак "мінус" у формулі (7.2) є відображення того факту, що коли заряди виходять з об'єму, то кількість зарядів у цьому об'ємі зменшується і похідна за часом, є величина від'ємна.

Таким чином, ми переконалися, що рівняння безперервності (7.1) виражає закон збереження заряду і що рівняння Максвела (5.1)-(5.4) сумісні з цим законом (тому що (7.1) – наслідок рівняння Максвела).

Зауваження. В електрично ізольованій електромагнітній системі заряди з об'єму V не витікають. Тому на замкнутій поверхні S електричний струм відсутній, тобто │_S = 0. Тоді замість (7.2) одержуємо:

чи ,

тобто заряд такої системи не змінюється.

Розглянемо тепер закон збереження енергії для електромагнітних явищ. Покажемо, що цей закон міститься (неявно) у рівняннях Максвела (5.1)-(5.4) і одержимо кількісне вираження для нього. Для цього помножимо скалярно рівняння (5.2) на вектор , рівняння (5.1) – на вектор і віднімемо з першого знайденого рівняння друге. У результаті одержимо співвідношення:

яке після застосування до лівої частини формули векторного аналізу:

(7.3)

можна записати у вигляді:

(7.4)

скориставшись очевидними тотожностями:

,

перепишемо (7.4) у вигляді:

,

чи, розділивши ліву і праву частини на ₀, у вигляді:

(7.5)

Для спрощення запису (7.5) уведемо формально позначення:

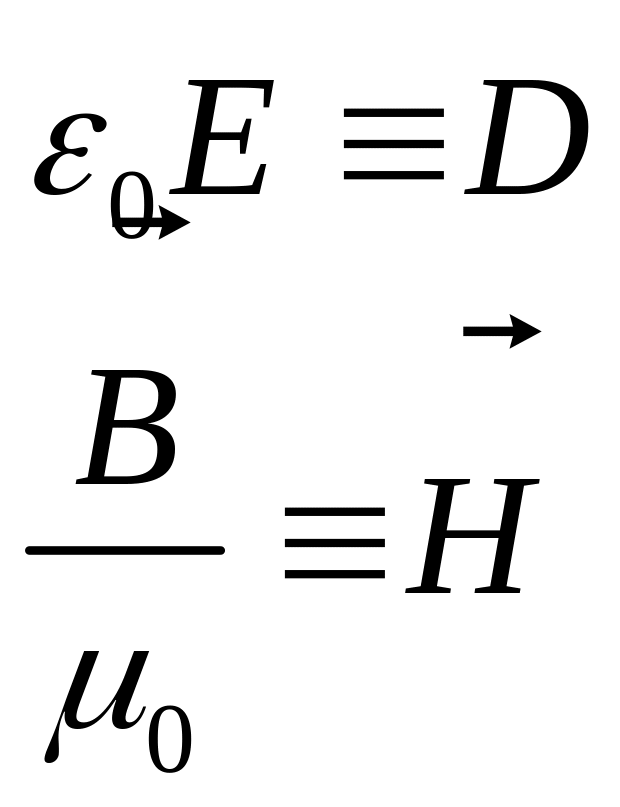(7.6)

після чого (7.5) записується в більш "симетричному" вигляді:

(7.5^/)

Далі, уводячи позначення:

(7.7)

(7.8)

перепишемо (7.5^/) у компактній формі

, (7.5^//)

зручної для з'ясування фізичного змісту цього співвідношення.

Найпростіше з'ясувати фізичний зміст доданка у формулі (7.5^//):

(7.9)

де є сила, що діє з боку електричного поля на заряд  в одиниця об'єму. Ясно тоді, що (7.9) є вираз для роботи, що виконує електричне поле по переміщенню зарядів в одиниця об'єму за одиницю часу. З іншої сторони ми знаємо, що магнітне поле не виконує роботи по переміщенню зарядів (це видно з закону Ампера: відкіля випливає, що магнітна сила перпендикулярна швидкості руху заряду  і отже робота магнітного поля ). Тому можна вважати, що (7.9) є робота електромагнітного поля по переміщенню зарядів в одиниця об'єму за одиницю часу. Таким чином, електромагнітне поле має енергію і цю енергію може перетворюватися в кінетичну енергію зарядів. Може відбуватися і зворотний процес  випромінювання електромагнітний хвиль зарядами, що рухаються. Відповідно до (7.9) вираз:

(7.10)

є робота електромагнітного поля по переміщенню зарядів у довільному об'ємі V за одиницю часу.

Для з'ясування фізичного змісту рівняння (7.5^//) перетворимо його до інтегрального виду, проінтегрувавши його по довільному, але фіксованому об'єму V:

Переходячи в останньому доданку правої частини до інтегрування по поверхні S за допомогою формули (2.19), одержуємо співвідношення:

, (7.11)

яке є інтегральна форма запису співвідношення (7.5^//).

Покажемо тепер, що співвідношення (7.5^//) і (7.11) є математичні вирази закону збереження енергії. Паралельно з'ясуємо фізичний зміст величин , і , що входять у ці співвідношення. Для цього розглянемо дві часткові випадки електромагнітних систем.

1) Ізольована (замкнута) система. Тут ми розглядаємо таку фізичну систему (що складається з електромагнітного поля і зарядів), що не може обмінюватися енергією з іншими системами, що знаходяться поза виділеним об'ємом V. Це буває тоді коли розглянута система не взаємодіє з іншими системами і на поверхні S, що обмежує об'єм V, електромагнітне поле відсутнє, тобто │_S = │_S. У цьому випадку вектор (7.8) на поверхні S дорівнює нулю, отже і співвідношення (7.11) для ізольованої системи приймає вигляд: (7.12)

так як згідно (7.10) у правій частині (7.12) стоїть робота виконувана електромагнітним полем по переміщенню зарядів в об'ємі V за одиницю часу, то (відповідно до загального закону збереження енергії) ліворуч у (7.12) повинне стояти відповідна зміна енергії електромагнітного поля за одиницю часу. Таким чином, ми дійдемо висновку, що інтеграл визначає енергію електромагнітного поля в об'ємі V, а величина , визначенна формулою (7.7), є густиною енергії електромагнітного поля, тобто енергія електромагнітного поля в одиничному об'ємі.

2) Відкрита система без зарядів. Тепер розглянемо електромагнітну систему, що не є ізольованою і складається тільки з електромагнітного поля в об'ємі V (тобто не містить електричних зарядів). Для такої системи  = 0, отже і . У цьому випадку (7.11) записується у вигляді:

(7.13)

Ми установили, що в лівій частині (7.13) стоїть зміна енергії електромагнітного поля в об'ємі V за одиницю часу. Оскільки енергія зникнути не може і поле не робить роботи по переміщенню зарядів у розглянутому випадку, то інтеграл по поверхні в правій частині (7.13) повинний визначати енергію електромагнітного поля, що витікає з об'єму V за одиницю часу, тобто є потік енергії електромагнітного поля через замкнуту поверхню S за одиницю часу. Звідси випливає фізичний зміст вектора це є густина потоку енергії електромагнітного поля, тобто кількість енергії поля, що протікає в одиницю часу через одиничну площадку, перпендикулярну вектору . Вектор , визначений формулою (7.8) називається вектором Умова-Пойтинга. Знак "-" у (7.13) указує, що енергія поля в об'ємі V зменшується, якщо потік енергії спрямований назовні з об'єму (тобто якщо потік позитивний  (див. визначення потоку вектора (2,15)).

У загальному випадку довільної електромагнітної системи співвідношення (7.11) показує, що зміна енергії електромагнітного поля в деякому об'ємі V дорівнює електромагнітної енергії, що витікає з V, і роботі виконаної полем по переміщенню зарядів усередині V. Таким чином, співвідношення (7.11) і, отже , співвідношення (7.5^//) є інтегральна і диференціальна форма запису закону збереження енергії для електромагнітних явищ.

Зауваження 1. Електромагнітне поле поряд з енергією володіє також і імпульсом. Імпульс електромагнітного поля в об'ємі V можна представити у вигляді інтеграла по об'єму від густини імпульсу (подібно тому як енергія W поля в об'ємі V можна виразити через густину енергії: ):

(7.14)

Докладний аналіз (який ми тут опускаємо) показує, що густина імпульсу електромагнітного поля задається виразом:

(7.15)

де в останньому з рівностей (7.15) ми скористалися формулою (6.11) для електродинамічної постійної (швидкості поширення електромагнітних хвиль у вакуумі). Формула (7.15) установлює природний зв'язок між густиною імпульсу і густиною потоку енергії електромагнітного поля.

Зауваження 2. Поряд з енергією й імпульсом електромагнітне поле володіє і моментом імпульсу , що виражається через густину моменту імпульсу інтегралом:

(7.16)

Подібно формулі для механічного моменту імпульсу матеріальної точки, що має імпульс, густина моменту імпульсу електромагнітного поля зв'язана з густиною імпульсу поля аналогічною формулою:

= (7.17)

де в останніх двох рівностях ми скористалися виразом (7.15).

Зауваження 3. У цьому §7 ми переконалися, що класичні фізичні поля (електромагнітне, і  за аналогією  гравітаційне) характеризуються тими ж фундаментальними фізичними характеристиками (енергією, імпульсом, моментом імпульсу), що і механічні системи (класична речовина). Це підтверджує єдність двох форм фізичної матерії (речовини і поля) на рівні класичного (неквантового) розгляду. Повна єдність (синтез) у розумінні речовини і поля досягається тільки в квантово-польовій картині світу (у понятті так називаного квантового поля).

Додаток до частини 1

У цьому додатку ми зробимо ряд зауважень про застосування законів електродинаміки вакууму до вивчення електромагнітних явищ у матеріальних середовищах (газах, рідинах, твердих тілах). Єдина мета цього Додатка  показати, яким шляхом з'являються нові характеристики електромагнітного поля і , що були у випадках вакууму формально уведені визначеннями (7.6). Докладні докази результатів, що приводяться, ми тут не приводимо.

Застосування законів електродинаміки (5.1)  (5.4) до опису електромагнітних явищ у матеріальних середовищах (у речовині) засновано на наступних основних положеннях класичної електронної теорії Лоренца:

1) матеріальне середовище розглядається як система мікроскопічних зарядів, що рухаються, (наприклад, протонів і електронів);

2) мікроскопічні електромагнітні поля, створювані цими зарядами, описуються рівняннями вакууму (5.1)  (5.4), тобто рівняння мікроскопічної електродинаміки матеріальних середовищ записуються у вигляді:

(П.1)

де мікроскопічні характеристики , , , дуже швидко змінюють свої значення як при зміщенні точки спостереження навіть на дуже малі відстані (порядку розмірів атомів), так і при найменшій зміні часу спостереження t (порядку часу протікання атомних процесів). Тому докладний мікроскопічний опис структури електромагнітного поля в речовині є дуже складна задача. На щастя, такий докладний опис найчастіше є і зайвим (наприклад, тіло макроскопічних розмірів не "почуває" флуктуацій поля в межах атома і реагує на електромагнітне поле так, начебто на нього діє поле, усереднене по багатьом атомам). Тому часто застосовують мікроскопічний спосіб опису полів, коли дискретним характером складу речовини зневажають і проводять усереднення всіх характеристик по фізично малому об'ємі і фізично малому проміжку часу. Проводячи таке усереднення рівнянь (П.1), одержуємо систему рівнянь макроскопічної електродинаміки:

(П.2)

(П.3)

(П.4)

(П.5).

де і є (на відміну від частини 1) усереднені (мікроскопічні) характеристики поля, а , є середні (макроскопічні) значення густини заряду і густини струму.

З макроскопічної точки зору середню густину заряду зручно розділити на дві частини:

(П.6)

де  – середня густина вільних зарядів (розподіл таких зарядів не залежить від і найчастіше вважається заздалегідь відомою функцією координат і часу), а  середня густина зв'язаних зарядів (це заряди атомів і молекул які не можуть переміщатися на мікроскопічні відстані і залежить від ). Докладний аналіз явищ поляризації середовища показує, що:

` , (П.7)

де є вектор поляризації середовища (дипольний момент одиниця об'єму середовища).

Підставляючи (П.6) і (П.7) у рівняння (П.4), перепишемо його вигляді:

(П.4^/)

чи ,остаточно, у вигляді:

(П.4^//)

де ми ввели нову характеристику електричного поля в матеріальному середовищі  вектор електричної індукції  по визначенню:

(П.8)

Основною характеристикою електричного поля є його напруженість , тому що 1) створюється всіма зарядами незалежно від їхньої природи (вільні вони чи зв'язані); 2) сила, що діє на заряд, визначається саме напруженістю електричного поля (див. 2.1). Вектор електричної індукції є допоміжна характеристика електричного поля, тому що створюється тільки вільними зарядами (див.П.4^//). Для безмежних, однорідних середовищ узагалі не залежить від виду середовища, тому що цілком визначається вільними зарядами. Для вакууму з (П.8) випливає , чим ми і скористалися формально у формулі (7.6).

Далі з макроскопічної точки зору, у залежності від природи руху зарядів середню густину струму з рівняння (П.2) зручно розділити на три частини:

(П.9)

де – середня густина струму провідності (у типових випадках провідних середовищ зв'язано з напруженістю електричного поля законом Ома в диференціальній формі: , де – питома електропровідність середовища, а – стороння електрорушійна сила джерел струму, якщо такі маються). Величина є середня густина поляризаційного струму, зв'язаного з рухом зв'язаних зарядів при поляризації середовища під дією електричного поля; легко показати, що зв'язано з вектором поляризації співвідношенням:

(П.10)

Величина є середня густина струму намагніченості – це середнє значення густини молекулярних струмів. Можна показати, що вектор зв'язаний з вектором намагніченості (тобто магнітним моментом одиниця об'єму середовища) співвідношенням:

(П.11)

Підставляючи тепер вираження (П.9)  (П.11) у рівняння (П.2) переписуємо останнє у вигляді, чи, після перегруповування доданків, у вигляді:

чи, після перегрупування доданків, у вигляді:

(П.2^/)

Уводячи визначення:

(П.12)

і використовуючи (П.8), переписуємо (П.2^/) в остаточному вигляді:

(П.2")

Визначенням (П.12) ми ввели нову характеристику магнітного поля , що називається напруженістю магнітного поля. Магнітна індукція є основною характеристикою магнітного поля тому що 1) породжується рухом зарядів будь-якої природи (як вільних, так і зв'язаних); 2) визначає (відповідно до закону Ампера) силовий вплив магнітного поля на заряди, що рухаються, (струми). Напруженість є допоміжною характеристикою магнітного поля, тому що породжується рухом не всіх зарядів, а тільки вільних зарядів (це видно з (П.2")). Вектор уводиться для спрощення розрахунків при розгляді електромагнітних явищ у матеріальних середовищах. У вакуумі немає молекулярних струмів, тому ,і визначення (П.12) для вакууму збігається з формальним визначенням (7.6). Підкреслимо, що при розгляді електромагнітних явищ у вакуумі немає ніякої фізичної причини для використання характеристики : ми використовували її в §7 чисто формально, тобто тільки для запису результатів у компактній формі.

Випишемо тепер ще раз систему рівнянь (П.2"), (П.3), (П.4") і (П.5)

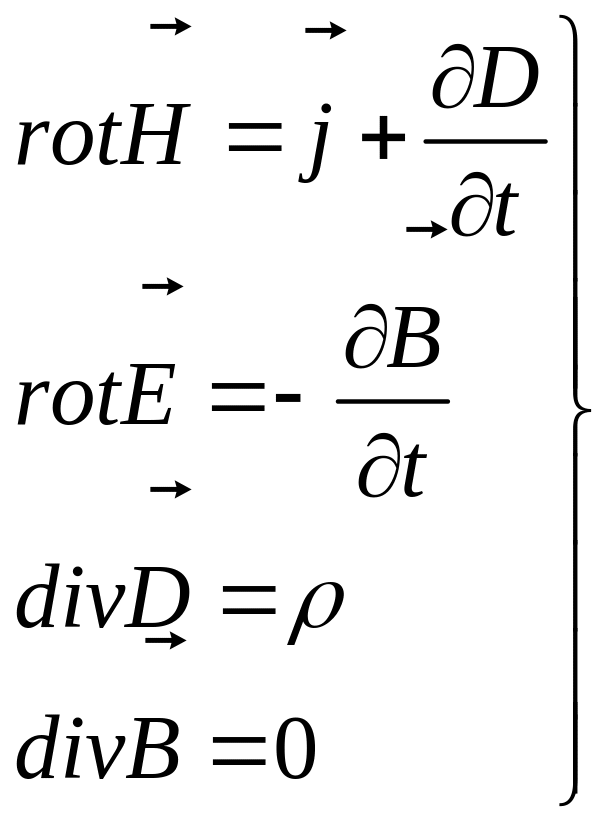(П.13)

Це є рівняння макроскопічної електродинаміки і називаються рівняннями Максвела. У цьому зв'язку відзначимо , що рівняння макроскопічної електродинаміки (П.10) називається рівняннями Максвела-Лоренца вони мають такий же вигляд, як і рівняння Максвела для електродинаміки вакууму (5.1)-(5.4).

Зауваження 1. Система рівнянь (П.13) не є повною, тобто її недостатньо для визначення всіх характеристик електромагнітного поля в матеріальному середовищі. До цих рівнянь необхідно додати співвідношення між і , а також між і , що задаються формулами (П.8) і (П.12), відповідно. Ці співвідношення називаються матеріальними рівняннями (чи матеріальними умовами). Так як і , то завдання матеріальних рівнянь зводиться до завдання явного вигляду функцій і . У найпростішому випадку однорідних і ізотропних середовищ ці функції мають відомий простий вигляд:

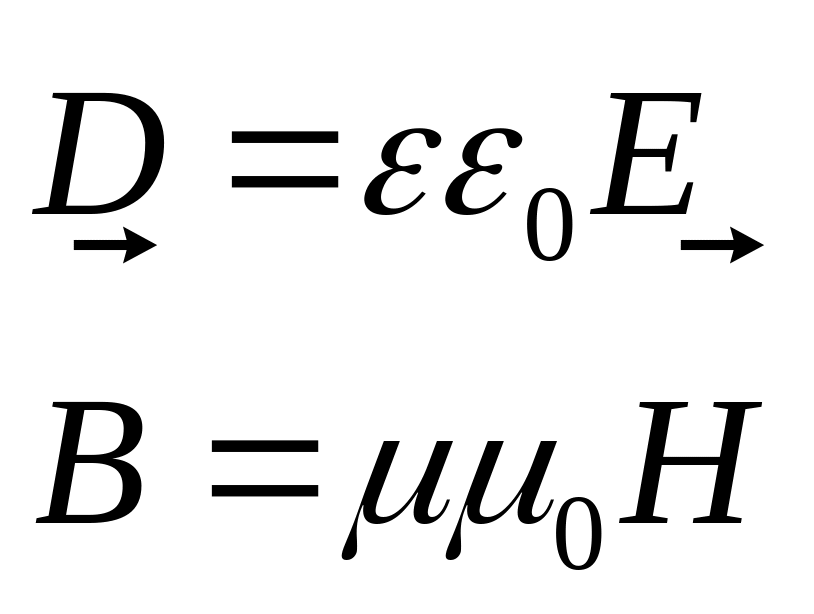(П.14)

і система рівнянь (П.13) разом з матеріальними умовами (П.14) є повною системою рівнянь макроскопічної електродинаміки однорідних і ізотропних матеріальних середовищ. Однак, для довільних (неоднорідних і анізотропних) середовищ явний вигляд матеріальних рівнянь:

(П.15)

у загальному випадку невідомий, функції (П.15) можуть мати дуже складний вигляд, що залежить від характеру (властивостей) середовища. Тому рівняння (П.15) задаються, як правило, феноменологично, тобто беруться з досвіду.

Зауваження 2. При одержанні фізичних рішень системи рівнянь (П.13) і (П.15) необхідно задати додатково відповідні постійні конкретної задачі –початкові і граничні умови. У багатьох важливих випадках (при наявності граничних поверхонь  границь роздягнула між різними середовищами) такими граничними умовами є співвідношення між нормальними і тангенціальними (стосовно поверхні розподілу) складовими векторів , , , , що легко одержуються (ми їх не приводимо) з відповідної інтегральної форми рівнянь (П.13).

Зауваження 3. Система рівнянь макроскопічної електродинаміки записана тут у системі одиниць СІ. У гауссовой системі одиниць рівняння (П.13)  (П.14) приймають наступний вигляд:

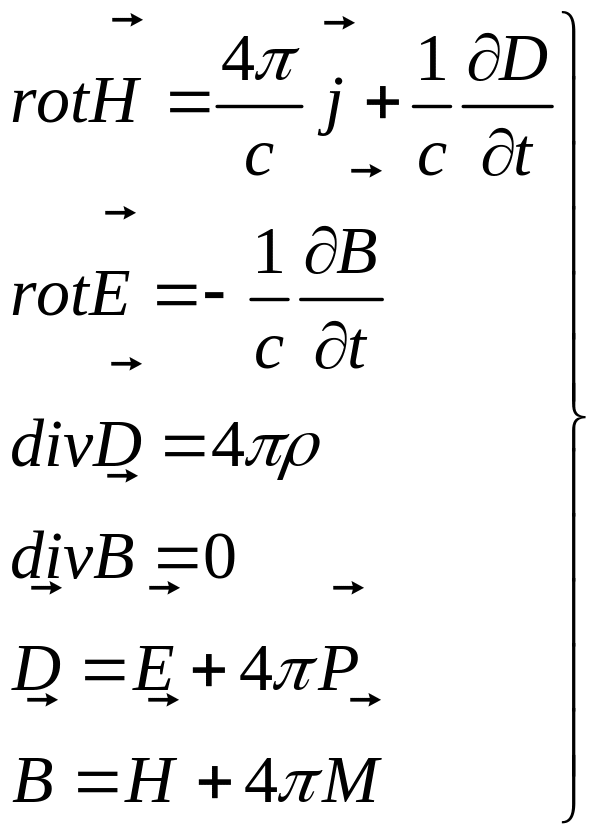(П.16)

де с  швидкість електромагнітних хвиль у вакуумі .

Зауваження 4. Зробимо одне зауваження методичного характеру. На нашу думку, класичну електродинаміку в педагогічному інституті раціонально викладати в послідовності тем (розділів), зображеної схематично на наступній структурно-логічній схемі:

Основні закони електродинаміки вакууму як узагальнення дослідних даних

Рівняння електродинаміки матеріальних середовищ

Врахування властивостей середовища

Електростатика

Магнітостатика

Квазістаціонарні

електромагнітні поля

Розподіл електромагнітних хвиль

Випромінювання електромагнітних хвиль

……………………………..

I

II

III

IV

V

VI

VII

Застосування рівнянь електродинаміки

Виклад електродинаміки в такій логічній послідовності дозволяє: 1) раціонально сполучити індуктивний (теми I-II ) і дедуктивний (теми III-VII) методи викладу; 2) методологічно правильно освітити зв'язок між електричним і теоретичним рівнем фізичних знань (див. частину 1); 3) акцентувати увагу студентів на основних законах електродинаміки; 4) підкреслити єдність методики застосування рівнянь Максвела до конкретних фізичних задач (теми III  VII); здійснити міжпредметні зв'язки з відповідним розділом курсу загальної фізики (тема I).