§ 5. Поверхні другого порядку

1. Поверхні обертання. Нехай у просторі задано прямокутну декартову систему координат і нехай рівняння

(33)

визначає деяку лінію в площині . Будемо обертати цю лінію навколо осі . Тоді кожна точка лінії

опише коло, а лінія – поверхню, яка називається поверхнею обертання.

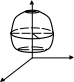Знайдемо рівняння поверхні обертання. Нехай точка належить лінії . Тоді

. (34)

Н

ехай точка лежить на колі , описаному точкою при обертанні лінії . Точки , лежать в одній площині , а як радіуси кола . Підставивши замість , а замість в рівність (34), дістаємо рівняння поверхні обертання

. (35)

2. Еліпсоїд. Обертаючи еліпс, заданий в площині рівнянням

,

навколо координатної осі , отримаємо рівняння еліпсоїда обертання

. (36)

Виконаємо рівномірний розтяг в разів, , вздовж осі абсцис:

, , .

Тоді всі точки еліпсоїда обертання (36) перейдуть в точки поверхні з таким рівнянням

,

де .

Поверхня, яка в деякій прямокутній декартовій системі координат має рівняння

, (37)

називається еліпсоїдом.

З рівняння (37) видно, що початок координат є центром симетрії еліпсоїда, а координатні площини – його площинами симетрії.

3. Конус другого порядку. Нехай в площині задано рівняння

пари прямих, які перетинаються. Тоді поверхня, отримана обертанням цих прямих навколо осі аплікат, має рівняння

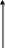
і називається прямим круговим конусом. Розтяг вздовж осі абсцис переводить прямий круговий конус в поверхню, задану рівнянням

. (38)

Поверхня, яка в деякій прямокутній декартовій системі координат має рівняння (38), називається конусом другого порядку.

4. Однопорожнинний гіперболоїд. Будемо обертати гіперболу, задану в площині рівнянням

,

навколо її уявної осі, тобто осі . Поверхня обертання, яка при цьому отримується, називається однопорожнинним гіперболоїдом обертання і має рівняння

.

В результаті рівномірного розтягу вздовж осі отримується поверхня з рівнянням

. (39)

. (39)

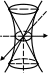Поверхня, яка в деякій прямокутній декартовій системі координат має рівняння (39), називається однопорожнинним гіперболоїдом.

На поверхні однопорожнинного гіперболоїда лежить дві сім’ї прямолінійних твірних. Справді, перепишемо рівняння (39) так

.

Розкладемо кожну з обох частин цієї рівності як різницю квадратів:

.

Звідси,

. (40)

Позначивши спільне значення цих відношень через , дістаємо

(41)

При кожному фіксованому значенні (41) є загальними рівняннями прямої в просторі. Якщо числовий параметр пробігає всю числову вісь, то отримується однопараметрична сім’я прямих (41), кожна з яких лежить на однопорожнинному гіперболоїді (39).

Перепишемо пропорцію (40) таким чином

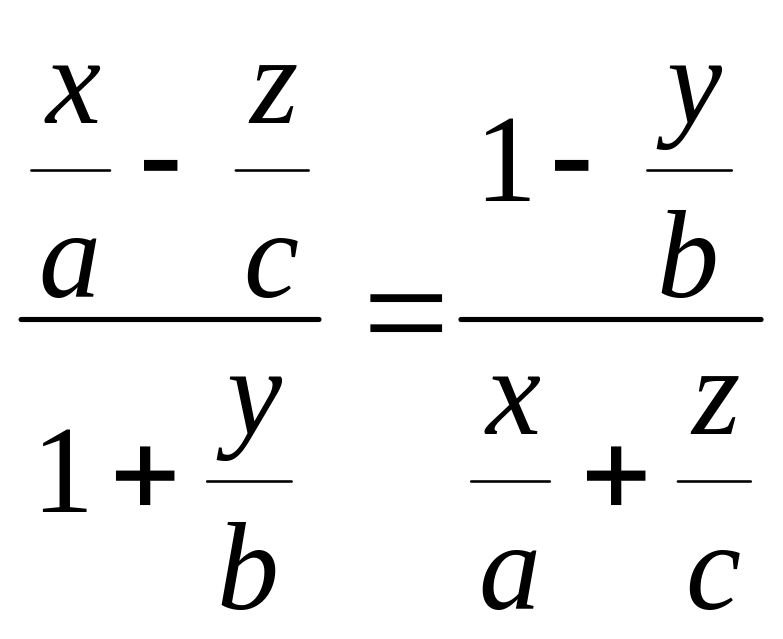
і позначимо спільне значення отриманих відношень через . В результаті дістанемо ще одну однопараметричну сім’ю прямолінійних твірних:

(42)

Розв’язавши відповідні системи рівнянь, неважко переконатися, що будь-які твірні одної й тої самої сім’ї не перетинаються, а будь-які дві прямі з різних сімей перетинаються, до того ж через кожну точку однопорожнинного гіперболоїда проходить рівно дві прямі – по одній з кожної сім’ї.

Якщо разом з гіперболою обертати і її асимптоти, то вони опишуть прямий круговий конус, який називається асимптотичним конусом гіперболоїда обертання. При рівномірному стиску гіперболоїда обертання прямий круговий конус стискається в деякий конус другого порядку, який називається асимптотичним конусом однорожнинного гіперболоїда.

5. Двопорожнинний гіперболоїд. Двопорожнинним гіперболоїдом обертання називається поверхня, яка отримується обертанням гіперболи

навколо її дійсної осі, тобто осі . За рівністю (35) отримуємо рівняння двопорожнинного гіперболоїда обертання

.

Після рівномірного стиску цієї поверхні вздовж осі отримуємо поверхню з таким рівнянням

. (43)

Поверхня, яка в деякій прямокутній декартовій системі координат визначається рівнянням (43), називається двопорожнинним гіперболоїдом.

Асимптотичний конус для двопорожнинного гіперболоїда визначається так само, як і для однопорожнинного.

6. Еліптичний параболоїд. При обертанні параболи

н авколо її осі симетрії – осі – дістаємо поверхню з рівнянням

,

яка називається параболоїдом обертання. Після стиску вздовж осі параболоїд обертання переходить в поверхню, яка має рівняння

. (44)

Поверхня, яка в деякій прямокутній декартовій системі координат має рівняння (44), називається еліптичним параболоїдом.

7. Гіперболічний параболоїд. Поверхня, яка в деякій прямокутній декартовій системі координат має рівняння

, (45)

називається гіперболічним параболоїдом.

Зауважимо, що гіперболічний параболоїд не можна отримати обертанням якої-небудь лінії.

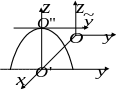Дослідимо форму гіперболічного параболоїда, проводячи перетини цієї поверхні площинами при різних значеннях . В площині виберемо прямокутну декартову систему координат з початком у точці . Відносно цієї системи координат лінія перетину має рівняння

. (46)

Це рівняння параболи з вершиною у точці , яка має координати в системі координат . Зауважимо, що у вихідній системі координат точка має координати . Вісь цієї параболи паралельна до осі , а знак мінус у лівій частині рівняння (46) означає, що вітки параболи напрямлені вниз. Зауважимо, що якщо перенести початок координат у площині в точку за формулами

; ,

то в новій системі координат рівняння (46) має вигляд

,

тобто не залежить від . Це означає, що всі перетини гіперболічного параболоїда площинами є однаковими параболами.

Будемо змінювати величину і прослідкуємо за переміщенням точки при зміні . З того, що точка у вихідній системі координат має координати , випливає, що точка лежить на лінії

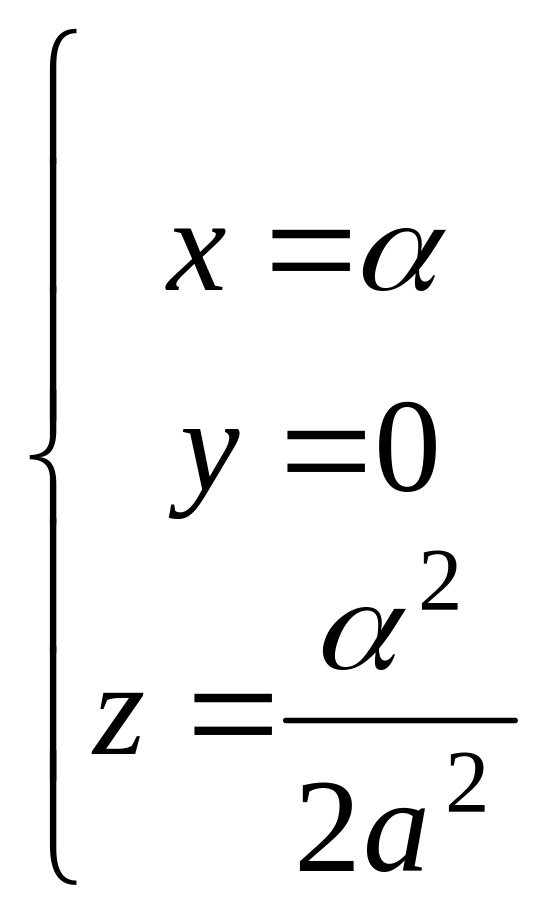
або

Очевидно, що ця лінія лежить у площині з рівнянням і є параболою, вершина якої збігається з точкою . Вісь симетрії цієї параболи збігається з віссю , до того ж вітки параболи напрямлені вгору.

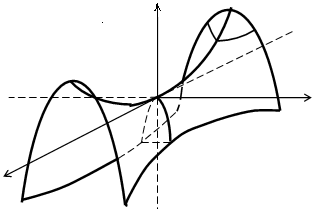На підставі викладеного можна вказати спосіб побудови гіперболічного параболоїда. Задамо дві параболи, які лежать у взаємно перпендикулярних площинах та , осі яких збігаються з віссю , вітки парабол напрямлені в протилежні сторони, а вершини збігаються з початком координат . Якщо одну з цих парабол переміщувати так, щоб її вершина ковзала по другій, а площини рухомої параболи були паралельними, то рухома парабола опише гіперболічний параболоїд.

Перетин гіперболічного параболоїда площиною є гіперболою. Справді, перетин визначається системою рівнянь

або рівнянням

(47)

в системі координат площини з початком у точці . Зауважимо, що при гіпербола (47) вироджується в пару прямих, які перетинаються

, .

Гіперболічний параболоїд має дві сім’ї прямолінійних твірних. Справді, з рівняння (45) маємо

,

або

.

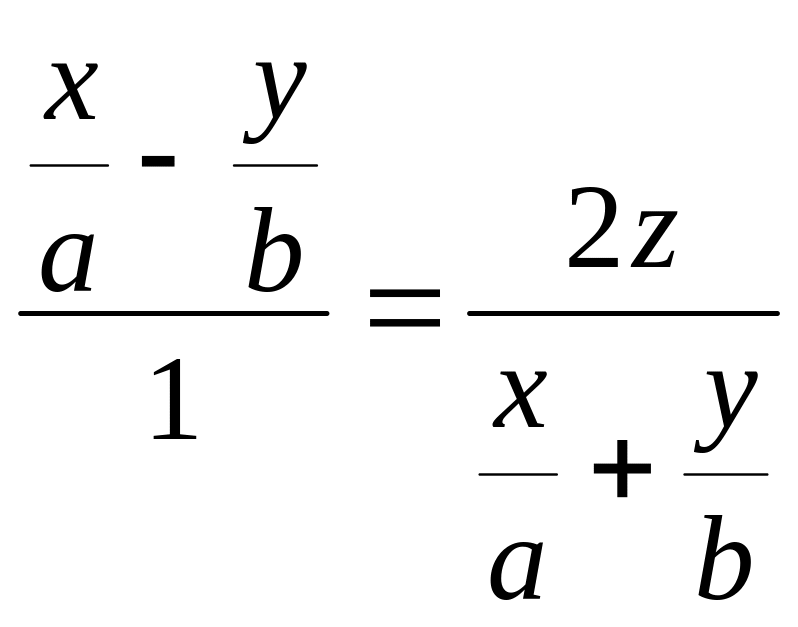Прирівнявши обидва відношення до , дістаємо

(48)

Друга сім’я прямолінійних твірних отримується з рівності

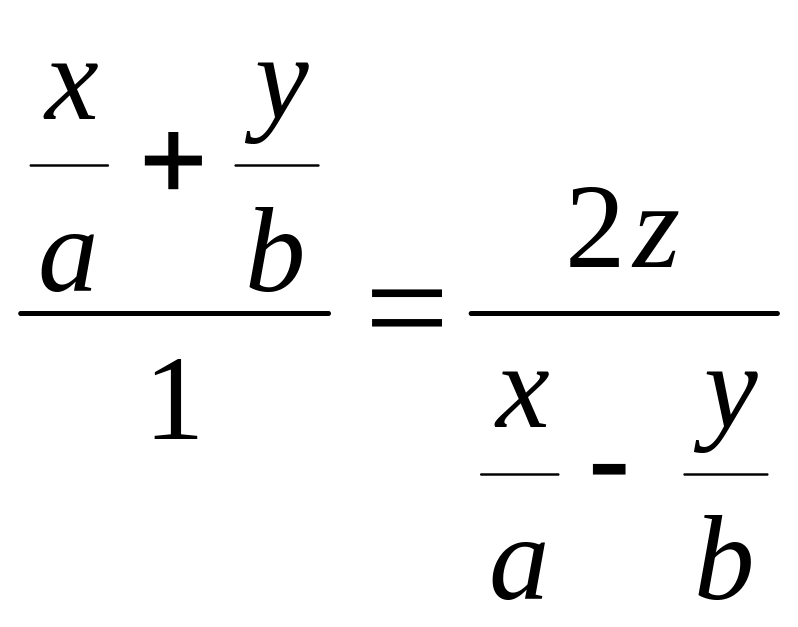
шляхом прирівнювання обидвох відношень до :

(49)

Зазначимо, що сім’ї прямолінійних твірних (48), (49) гіперболічного параболоїда мають такі самі властивості, що й сім’ї прямолінійних твірних однопорожнинного гіперболоїда.

8. Циліндри другого порядку. Є три типи циліндрів другого порядку:

1) еліптичний, який визначається рівнянням

, (50)

2) гіперболічний, який має рівняння

, (51)

3) параболічний, який задається рівнянням

. (52)

Циліндр другого порядку можна уявляти як поверхню, описану прямою, що перетинає лінію другого порядку і проходить перпендикулярно до її площини, при переміщенні цієї прямої вздовж даної лінії другого порядку. Будь-яка пряма, що лежить на поверхні циліндра, називається його твірною, а лінія другого порядку – його напрямною.