
- •Методические указания
- •Предисловие
- •Практическое занятие №6 случайные события и случайные величины
- •Контрольные вопросы
- •Практическое занятие №7 случайные процессы. Функции распределения и числовые характеристики
- •Контрольные вопросы
- •Практическое занятие №8 спектральная плотность случайного процесса. Узкополосные и широкополосные случайные процессы
- •Контрольные вопросы
- •Практическое занятие №9 преобразование случайных сигналов в радиотехнических устройствах
- •Контрольные вопросы
- •Практическое занятие №10 потенциальнаяпомехоустоéчивость систем связи
- •Контрольные вопросы
- •Практическое занятие №11 методы приема дискретных сигналов
- •Контрольные вопросы
- •Практическое занятие ¹12 скорость передачи информации по каналам связи
- •Контрольные вопросы
- •Практическое занятие №13 корректирующие коды
- •Контрольные вопросы
- •Значения функций
- •Табличные интегралы
- •Список литературы
- •Оглавление
Практическое занятие №7 случайные процессы. Функции распределения и числовые характеристики
Цель занятия:Изучение вероятностных характеристик (законов распределения вероятностей), числовых характеристик и свойств случайных сигналов и помех в каналах и системах связи.
Литература: [ 1 ] – стр. 28 – 38;
[ 2 ] – стр. 166 – 189;
[ 3 ] – стр. 161 – 172;
[ 4 ] – стр. 8 – 10;
[ 5 ] – стр. 133 – 138, 154 – 157.
Контрольные вопросы
Что называется случайной функцией?
Что называется случайным процессом?
Что называется реализацией случайного процесса? Примеры реализаций случайного процесса?
Что такое сечение случайного процесса? Что представляет собой случайный процесс в сечении?
Как определяется одномерная плотность распределения вероятностей случайного процесса? Что она показывает?
Что такое n-мерные функции распределения случайного процесса ? Зачем они нужны при описании случайных процессов?
Какой процесс называют чисто случайным? Как связаны n-мерная и одномерная функции распределения чисто случайного процесса?
Какие процессы называются марковскими? Какие функции распределения вероятностей используются для их описания?
Что называется математическим ожиданием, дисперсией и корреляционной функцией случайного процесса?
Что такое нормированная корреляционная функция и интервал корреляции? Как они вычисляются?
Какие случайные процессы называются стационарными в узком смысле? Какие в широком?
Чему равняется значение функции корреляции стационарного случайного процесса B(t) приt= 0 ?
Какие случайные процессы называются взаимно стационарными?
Чем отличается некоррелированность от независимости сечений случайных процессов?
Какие процессы называются эргодическими?
Как определяются числовые характеристики эргодического случайного процесса?
Как используется понятие эргодичности случайных процессов в инженерной практике? Примеры.
Задачи
7.1*.Построить график одномерной плотности распределения вероятности случайного напряжения, реализация которого показана на рис. 7.1.
Определить математическое ожидание и дисперсию усреднением по времени одной реализации и усреднением по множеству реализаций.
1 2 3 4 5 6 7 8 c=2 c=1 c=0 c=–2 c=–1 T1=T2 T1=2T2 T1=0,5T2
Рис. 7.1
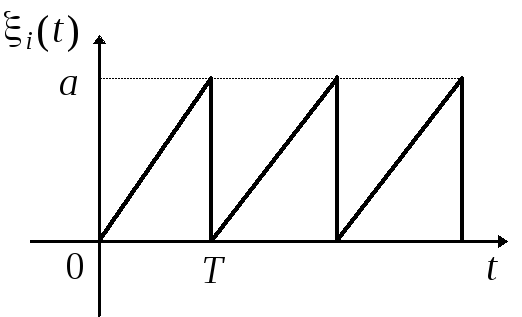
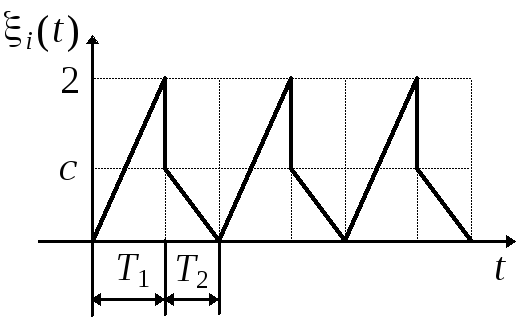 (а) (б)
(а) (б)
Определить их совместную плотность вероятности.
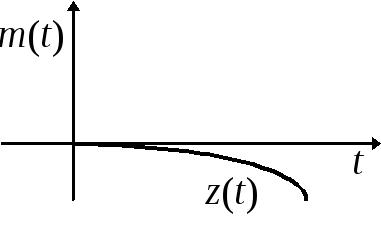
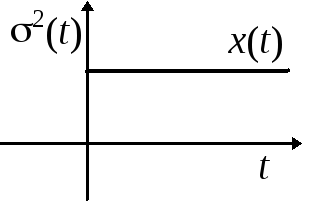
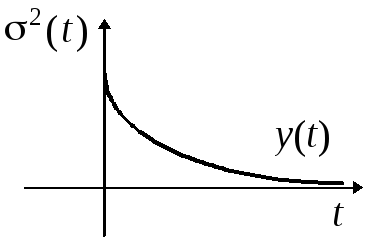
7.3.На рис. 7.2 изображены графики математического ожиданияm(t)дисперсииs2(t)для трех разновидностей случайной помехи, действующей в канале связи:x(t); y(t); z(t).Указать на графике области возможных значений каждой из случайной помехи, считая, что границы этих областей определяются значениями s2(t).
а) б) в)
Рис. 7.2.
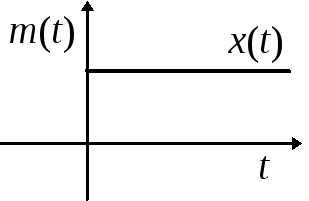
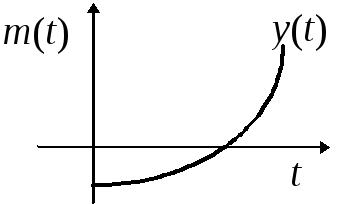

![]() .
.
Определить математическое ожидание m(t)и дисперсиюs2(t);изобразить на графике возможную область значений случайного процесса x(t),считая, что границы этой области соответствуют 3s.Изобразить также схематически деформацию закона распределенияW(x)во времени для трех моментов, для которых at1 = 0, at2 = 1, at3 = 3.
7.5. Показать, что если два случайных сигнала x(t) на входе и y(t)на выходе приёмного устройства в результате преобразований в приемном устройстве связаны линейной зависимостьюy=a±bx, то нормированная корреляционная функцияrxy = ± 1.
7.6.Найти одномернуюW1(x1,t)и двумернуюW2(x1,x2,t1,t2)плотности распределения вероятностей случайного сигнала, приходящего на приемную антенну тропосферной линии связи, если
x(t) = acoswt + bsinwt,
где w– постоянная угловая частота,
aиb– взаимно независимые случайные величины с нулевыми средними значениямиma = mb= 0 и дисперсиями s2a = s2b= s2.
7.7*. Определить постоянную составляющую, среднюю мощность переменной составляющей и функцию корреляции реализаций случайных сигналов, передаваемых в многоканальной системе связи:
1) xi (t) = asinw0t, 2) xi(t) = acosw0t,
3) xi(t) = asin(w0t + j), 4) xi(t) = acos(w0t + j),
5) xi(t) = a[1 + sinw0t], 6) xi(t) = a[1 + cosw0],
где j– случайная фаза с равномерным законом распределения
![]() .
.
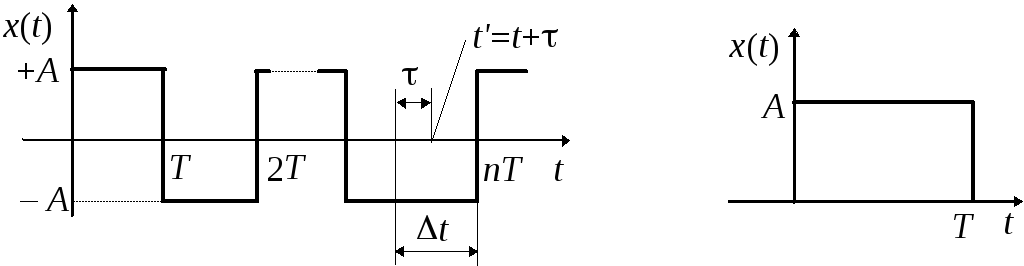
7.8**.Найти корреляционную функциюB(t)и интервал корреляцииt0случайного синхронного телеграфного сигнала, реализации которого имеют случайный равномерно распределенный сдвигDtотносительно начала координат, принимающий в дискретные моменты времени кратныеTзначения±Aс вероятностью 0,5 независимо от того, какое значение он имел на предыдущем участке (рис. 7.3, а),и одиночной телеграфной посылки (рис. 7.3, б).
а) б)
Рис. 7.3.
![]() ,
полученной в результате прохожденияx(t) через дифференцирующую цепь,
удовлетворяет условию:
,
полученной в результате прохожденияx(t) через дифференцирующую цепь,
удовлетворяет условию:
Bxy(t, t¢) = – Bxy(t¢, t),
т.е. при перемене местами аргументов меняется знак.
7.10.Флуктуационная помехаxв канале связи распределена по гауссовскому закону с характеристиками mxи sx. После прохождения двух параллельных приемных трактов многоканальной системы связи образуются случайные помехиyиz, связанные сxзависимостямиy=x2;z=x3. Найти взаимные корреляционные функцииBxy, Bxz, Byz.
7.11**.Найти корреляционную функцию, ковариационную функцию, нормированную корреляционную функцию и интервал корреляцииt0случайного стационарного телеграфного сигналаx(t),изображённого на рис 7.4 и представляющего собой последовательность прямоугольных импульсов равной амплитуды (равной 1) и случайной длительности. Распределения переходов (1®0 и 0®1) принимаются независимыми, т.е. распределение значенийx(t) (или 0,или 1) подчиняется закону Пуассона.
Рис. 7.4.
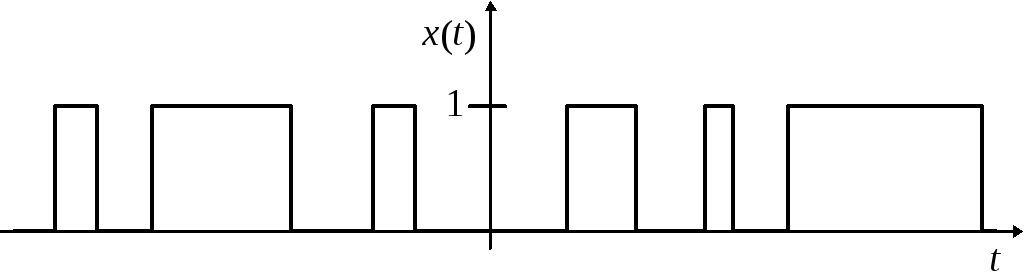
Задачу решить независимо от предыдущей; полученный результат сопоставить с результатом решения предыдущей задачи и показать возможность решения данной задачи на основе использования результата предыдущей.
Рис. 7. 5.
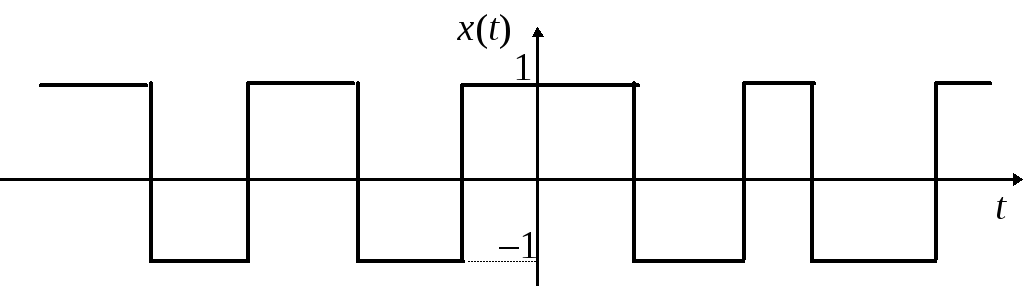
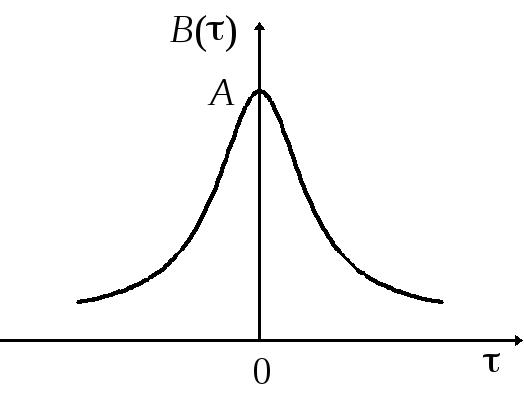
Найти корреляционную функцию.
Рис. 7.6.
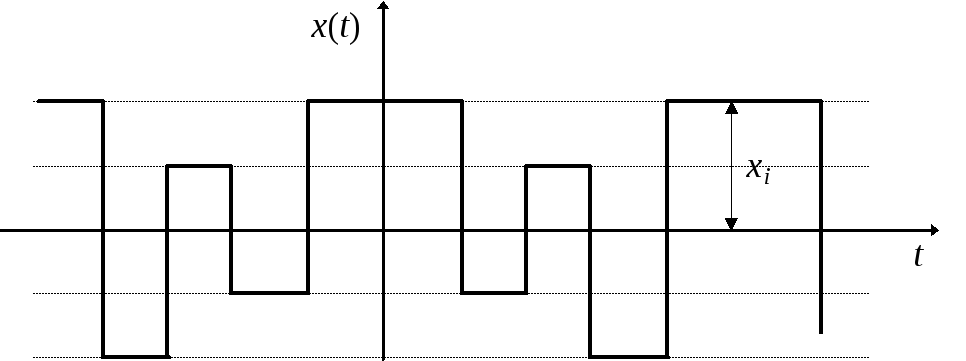
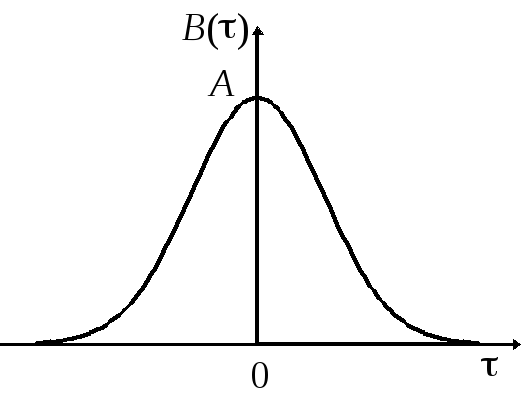
Рис. 7.7.
![]()
![]()

![]()
![]()
7.15.Найти корреляционную функцию периодического сигнала многоканальной системы связи, представленного рядом Фурье:
![]()
7.16.Найти функцию взаимной корреляции сигналаx1(t)произвольной формы и «узкого импульса», который может быть представлен функциейx2(t) = x0 d(t – t0).
7.17.Найти функцию взаимной корреляции двух зондирующих «узких» импульсов в гидроакустическом канале связи, сдвинутых между собою на времяDt.
7.18.Найти взаимную корреляционную функцию радиолокационных сигналов: периодической последовательности «узких» импульсов и сигналаx1(t) произвольной формы и с ограниченной длительностью.
7.19.Найти взаимную корреляционную функцию измерительных сигналовx1(t) иx2(t), изображённых на рис. 7.8:
Рис. 7.8.
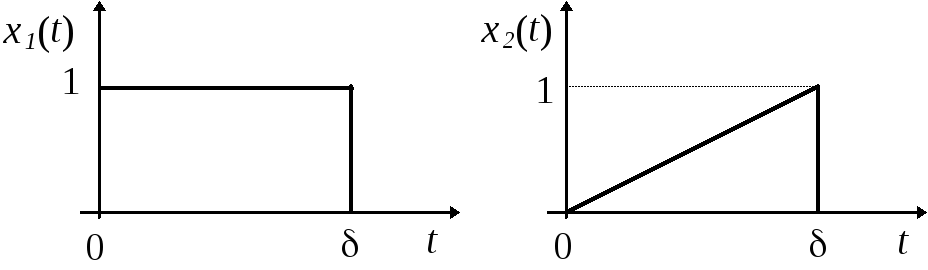
x(t) = acos(wt + j), (0 < t < s)
вместе с шумом, корреляционная функция которого имеет вид :
![]()
Сформулировать условия, при которых возможен приём слабого сигнала x(t) и составить структурную схему приемника. Считается, что сигнал и шум между собой некоррелированы.
7.21.Вычислить и изобразить графически корреляционную функцию одиночной кодовой последовательности прямоугольных импульсов длительностиtвида:
|
1 |
(+1,+1,+1,–1,+1) |
|
16 |
(+1,+1,+1,–1,+1,+1) |
|
2 |
(–1,+1,+1,+1,+1) |
|
17 |
(+1,+1,–1,+1,+1,+1) |
|
3 |
(+1,–1,+1,+1,+1) |
|
18 |
(+1,–1,+1,+1,+1,+1) |
|
4 |
(+1,+1,–1,+1,+1) |
|
19 |
(–1,+1,+1,+1,+1,+1) |
|
5 |
(+1,+1,+1,+1,–1) |
|
20 |
(–1,–1,+1,+1,+1,+1) |
|
6 |
(–1,–1,–1,+1,+1) |
|
21 |
(+1,+1,–1,–1,+1,+1) |
|
7 |
(–1,–1,+1,+1,+1) |
|
22 |
(+1,+1,+1,+1,–1,–1) |
|
8 |
(+1,–1,–1,–1,+1) |
|
23 |
(+1,+1,–1,+1,–1,+1) |
|
9 |
(+1,–1,–1,+1,+1) |
|
24 |
(+1,+1,+1,+1,–1,+1) |
|
10 |
(+1,+1,–1,–1,+1) |
|
25 |
(+1,+1,–1,–1,–1,–1,+1) |
|
11 |
(+1,+1,+1,–1,–1) |
|
26 |
(+1,+1,+1,+1,–1,+1,+1) |
|
12 |
(–1,–1,+1,–1,–1) |
|
27 |
(–1,–1,+1,+1,–1,+1,+1) |
|
13 |
(+1,–1,–1,–1,+1) |
|
28 |
(+1,–1,+1,–1,+1,–1,+1) |
|
14 |
(+1,+1,–1,–1,–1) |
|
29 |
(–1,–1,–1,+1,+1,+1,+1) |
|
15 |
(–1,+1,–1,+1,+1) |
|
30 |
(–1,–1,+1,–1,–1,–1,+1) |
Вычислить корреляционную функцию этих же последовательностей при периодическом повторении и сравнить с функцией корреляции одиночной последовательности.
7.22.Плотность вероятности двух случайных сигналов X и Y в канале связи выражается формулой :
W2(x,y) = Asin(x + y), (0 £ x £ p/2, 0 £ y £ p/2).
Определить постоянную A, затем найти функции распределения вероятностей:F2 (x,y), F1 (x), F1 (y).
7.23. По законам распределения, найденным в предыдущей задаче, найти вероятности, соответствующие следующим условиям:
|
1 |
2 |
3 |
|
x<p/4 |
x<p/4,y<p/4 |
p/6 <x<p/4,p/6 <y<p/4 |
7.24.Передаются два случайных сигнала X и Y, известна связь между ними и случайным параметромj:
x = сosj; y = sinj.
Случайный параметр jраспределен равномерно в интервале[–p; p]. Найти нормированную корреляционную функцию rxy(Dj).
7.25.Случайная помеха в канале связи характеризуется гауссовским распределением мгновенных значений
![]()
Найти закон распределения помехи z=x1–x2, еслиx1иx2мгновенные значения помехи, являющиеся по условию независимыми случайными величинами.
7.26Задана плотность распределения вероятностей двух случайных сигналовx(t) и y(t):
W2(x,y) = 0,5 sin(x+y), (0 £ x £ p/2 ; 0 £ y £ p/2).
Найти математическое ожидание, дисперсию, функцию взаимной корреляции случайных сигналов X и Y, построить корреляционную и нормированную корреляционную матрицы.
7.27.Заданы сигналыy1иy2, которые образуются в результате преобразования сигналовx1иx2в канале связи:
y1=ax1+bx2;y2= (x1+x2)2;
Найти Якобиан и установить, являются ли сигналы y1иy2независимыми.
Примечание:Для аудиторной работы с подробным анализом результатов решения рекомендуются задачи 7.1, 7.3, 7.8, 7.21. обратить внимание на возможность применения выводов из результатов решения задач 7.8 и 7.21 для повышения помехоустойчивости систем связи.
*При решении задач, отмеченных*, рекомендуется составить программу на алгоритмическом языке ЭВМ.
**Решение задач, отмеченных**, рекомендуется проиллюстрировать структурной схемой алгоритма.
