5.5. Інформаційна стійкість

Вказані вище умови не містять вказівок, яким чином здійснити їх практично при розробці системи і, тим більше, при розробці процедур самовдосконалення системи. Зрозуміло лише, що якщо складність формальної конструкції виявляється нижчою за нижню межу - ми отримуємо скінчений автомат, якщо вище верхньої - конструкцію, діагностика якої вимагає перебору всіх її станів, тобто створення звичайно-автоматної моделі, свідомо занадто великої, щоб її можна було реалізувати.

Дуже цікавим з практичної точки зору було б визначення деяких чисельних, таких, що нехай навіть мають непрямий характер критеріїв і оцінок складності, придатних для використання в розробці мов для систем класу, що цікавить нас.

Розглянемо процеси, що відбуваються в деякій системі високого рівня. Зокрема, дослідимо акт звернення до системи і акт поповнення інформаційної бази.

Акт звернення до системи. Нехай система має в своєму розпорядженні деяку інформацію, що змістовно є деяким числом М об’єктів (описів), зв’язаних N зв’язками і що посідають деяку кількість біт пам’яті. Запит полягає у вказівці групи (зазвичай одної) з об’єктів із вимогою пошуку і видачі m об’єктів і n зв’язків, при цьому відповіддю є m₁ об’єктів і n₁ зв’язків із похибкою івідповідно. Наступним кроком може бути уточнення запиту, що призводить до видачіm₂ об’єктів і n₂ зв’язків із помилкою іі так далі, до деякого задовольняючого користувача значення. Взагалі кажучи, правильно діюча система повинна при деякому значенні досягти деякої максимальної точності і при подальших спробах уточнення запиту залишатися в межах деякої допустимої девіації, що еквівалентно виходу системи на гомеокінетичне плато.

Інтуїтивно зрозуміло (практикам знайома ситуація), що у разі надмірно великого числа зв’язків між об’єктами уточнення запиту може призводити до видачі як відповідь все більш широкого класу об’єктів, що не мають відношення до запиту, тобто до збільшення .

В період введення в стрій вже перших крупних інформаційно-довідкових систем розробники зіткнулися із наступним явищем. У міру накопичення інформаційного банку на початку випадково, а потім регулярно стала повторюватися одна і та ж ситуація. Користувач, прагнучи отримати якомога точнішу відповідь, збільшував число додаткових (уточнюючих) запитів, але, починаючи з деякої їх кількості I, замість зменшення отримував все більше число об’єктів, тобтозбільшувалися (інколи монотонно, частіше цей процес був квазіперіодичним відI). Вихід із становища був знайдений досить швидко: за з’ясованими емпірично чисельними критеріями було обмежене число взаємозв’язків між елементами бази даних і вказане явище до деякої міри перестало турбувати користувачів і розробників.

Досить часто вказане обмеження на число взаємозв’язків (точніше кажучи, система обмежень) інтерпретується як емпірична оцінка деякої об’єктивної “функції цінності інформації”. Така точка зору широко поширена як у вітчизняній, так і зарубіжній літературі. Відзначимо, що її не можна плутати з іншим відомим і настільки ж методологічно невірним твердженням про виникнення інформації лише в наборі “чоловік - контекст – дані”. Останнє твердження не може бути прийняте, бо воно зводить інформацію до суб’єктивного існування замість того, щоб розглядати суб’єктивність оцінки інформації.

Прикладна теорія ІСУ виходить з наступних посилань:

• ніякої “об’єктивної оцінки істинності”, “функції цінності” тощо. не існує, локальність оцінки інформації показана вже при розборі ієрархії підсистем. Можна сказати, що “цінність” інформації (а не сама інформація) завжди існує лише в даному контексті і є локальним породженням взаємодії трійки “користувач-задача-вміст бази”;

• існування “оцінки істинності” чи “цінності інформації” у вигляді деякого скінченого набору ефективно обчислюваних функцій означало б, що ми побудували деяку квазімонотонну шкалу цінності “ВСЬОГО”, і тоді використаний набір оцінюючих процедур годився б апріорі для будь-якої системи, будь-якої задачі, будь-якого користувача;

• явище “інформаційної нестійкості” бази є єдиним що об’єктивно існує і доступним спостереженню і вимірюванню фактом, придатним для побудови загальних оцінок складності структури інформаційної бази. Оскільки смисловій оцінці відповіді завжди передує її отримання, тобто взаємодія зі системою, а їй, у свою чергу, передує заповнення бази, критерії завжди необхідно виявляються апріорними.

Побудуємо демонстраційну модель динаміки інформаційної структури системи. Зробимо наступні припущення:

• деякий засіб, маючи перед собою задачу (контекст) і відповідь системи, здатний абсолютно точно і швидко сформулювати свої побажання, тобто його моделлю є формальний компаратор;

• механізм обробки запитів не пропускає неприпустимих запитів і не втрачає корисної інформації. У такому разі його моделлю може служити ідеальний інтегратор;

• механізми доступу до інформації реалізовані коректно, тобто не втрачають інформації, і, таким чином, можуть бути змодельовані аперіодичною ланкою;

• “функція розстановки”, тобто залежність виходу (відповіді) від входу (суми запитів) представлена деякою шматково-гладкою залежністю y = f(x), лежачою між прямими y=kminx, y=kmaxx.

Тоді демонстраційна модель прийме вид, показаний на рис.5.1:

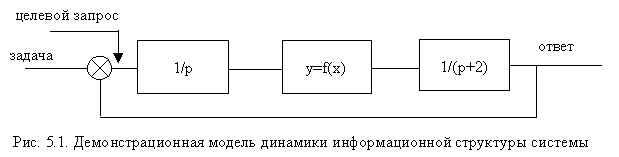
При малих сигналах (еквівалент “локальних” запитів) система може бути представлена рівняннями ; y=f(x).

Аналогом коефіцієнта передачі нелінійної ланки в нашому випадку є , тобто число зв’язків даногоi-го об’єкта, де - номер аспекту, за яким проводиться пошук.

Зрозуміло, така інтерпретація моделі допустима лише у разі незалежності аспектів (тобто, у термінології стежачих систем, за відсутності перехресних зв’язків між контурами, що моделюють кожний з аспектів).

Якісно набутих значень k_min і k_max для системи, що має l аспектів – “координат”, можна інтерпретувати таким чином.

При кількість схожих по кожній з “координат” об’єктів занадто мала, що приведе до “стрибків” пошукового механізму по координатах з огляду на те, що докладність просто відсутня.

При навпаки, подробиць занадто багато, тобто пошуковий механізм тоне в деталях.

У точнішій постановці необхідно врахувати багато упущених тут факторів, зокрема, взаємозв’язок аспектів, неідеальність користувача як елементу порівняння, складнішу структуру механізмів обробки запитів і організації доступу до бази. Приведена тут модель має лише демонстраційний характер. Проте вже сам факт можливості створення моделі інформаційної стійкості дає нам деяке обґрунтування можливості пошуку формального інструменту для управління етапом реорганізації інформаційної бази.

Акт поповнення інформаційної бази. У цьому акті відбувається збільшення числа об’єктів і зв’язків в інформаційній базі. Проводячи поповнення, ми лише повинні стежити за стійкістю системи, причому зробити це можна автоматично на підставі прийнятої моделі і відомих алгоритмів аналізу систем автоматичного регулювання.

Постановка задачі автоматизації розміщення об’єктів в інформаційній базі як задача дослідження стійкості, очевидно, є єдино прийнятною, оскільки дозволяє уникнути залучення таких ефемерних понять, як “функція цінності інформації”, “семантична вартість” тощо.

Дійсно, апріорна інформація в кожному акті поповнення, а тим більше при проектуванні системи, “цінність” чи “корельованість” майбутньої смислової начинки просто дорівнює нулю. Звідси випливає закономірний висновок про те, що при початку робіт із проектування ми повинні мати або універсальну структуру зберігання знань, або використовувати стартовий набір інформаційних записів і стартову базу знань. Перше неможливе, друге практично нездійсненне. Звичайно, і без стартової інформації можна придумати і обчислити відповідні оцінки структур зберігання, поставити завдання їх “оптимізації”, та яка теоретична правомочність цих дій хоч би тільки з позицій тієї ж задачі стійкості?

Таким чином, задача стійкості - єдина формальна модель, застосовна в нашій ситуації. Та ця ж постановка виявляється і засобом для вирішення проблеми в цілому. Спочатку можна взагалі не замислюватися про оптимізацію зберігання записів. Хай на деякому кроці поповнення інформаційної бази порушуються критерії стійкості. Чи означає це “закриття” системи, тобто неможливість збільшення обсягу інформації, що зберігається?

Ні в якому разі ні. Розв’язання достатньо тривіальне: створення ієрархічної структури, в якій кожний новий рівень може створюватися виходячи з своїх оцінок “функції розстановки” і стійкості, причому процес принципово можна зробити автоматичним за наступною схемою.

Перш за все на підставі вже наявних апріорних відомостей ідентифікуються моделі основних компонентів, тобто користувача, механізму обробки запитів, механізму доступу тощо.

Далі при поповненні банку розв’язується задача стійкості для уточненої моделі і обмежується число зв’язків між об’єктами.

При цьому в разі досягнення верхньої межі числа зв’язків проводиться автоматична генерація наступного чи наступних рівнів ієрархії інформаційного банку, які може бути і не мають смислового відокремлення, але необхідні для забезпечення стійкості системи.

У пропонованій моделі можливі і витонченіші постановки, вже відомі в практиці створення систем регулювання, наприклад, задача максимальної швидкодії і задача максимальної чутливості.

Останні, зокрема, призводять до якісно дуже цікавого вирішення – до системи, в якій реорганізація зв’язків відбувається не лише під впливом акта поповнення інформаційної бази, але і під впливом потоку запитів. Рішення напрошується за аналогією зі системами управління, що використовують шумові компоненти вхідного сигналу для підтримки коефіцієнта посилення на межі стійкості.

Ubi rerum testimonia adsunt, quid opus est verbis?

{95. У вільному перекладі з латинської: “Коли дані говорять самі за себе, навіщо програма?”}