5.4. Частотна оцінка

Звернемо увагу на наступні дві обставин, що є центральними для всіх подальших міркувань.

По-перше, система типу інформаційно-довідкової для задач управління повинна володіти інтелектуальними властивостями лише на деяких відрізках часу, протягом яких відбуваються модифікації інформаційної бази (знань), що еквівалентно усвідомленню системою нової функції розстановки. У кожному акті спілкування користувача зі системою з метою отримання інформації інтелектуальні властивості системи, що структуруються, не є строго необхідними.

Виходячи з конкретної постановки задачі для системи чи систем заданого типу, можна виділити відрізки часу статичні, тобто ті, на яких система нічим не відрізняється від скінченого автомата, і динамічні, тобто такі, на яких відбувається реорганізація системи, зокрема – реорганізація структури інтелектуальної бази, перевизначення інформаційних зв’язків.

По-друге, якщо система реалізована коректно на рівні програм і її поведінка кінцево-розпізнавана, зовсім не обов’язково, щоб її відповіді були завжди безпомилкові. Право на помилку давно визнане за інтелектуальними системами. У всякому разі, абсолютна повнота і правильність відповідей не повинні виходити з постановки задач створення як просто інформаційно-довідкової, так і інтелектуальної системи. І та і інша користуються інформацією від зовнішнього світу, яка може бути невизначеною чи суперечливою і, крім того, ці системи мають логіку своїх вирішень, що базуються на скінченному числі відомих ситуацій.

Це означає, з одного боку, що ми можемо припустити появу помилок у відповідях із частотою, що не перевищує деякого заданого рівня. Частотна оцінка використовується тут по суті задачі, бо на будь-якому скінченному числі актів спілкування зі системою ми маємо справу зі скiнченним числом об’єктів (ситуацій) і скінченою апроксимацією функції розстановки, так що використання граничного переходу до статистичних оцінок за ймовірністю представляється тут некоректним.

З іншого боку, у міру накопичення інформаційної бази і роботи з нею, вид функції розстановки по суті завдання створення високорівневої системи, очевидно, повинен змінюватися настільки суттєво, що різні реалізації її, що належать різним статичним інтервалам, можуть не належати до однієї рекурсивної множини і ця приналежність не може бути встановлена ніяким скінченним алгоритмом.

У цьому сенсі в теорії ІСУ доводиться мати справу з реалізацією скінченої апроксимації функції розстановки, яка по суті не є рекурсивною, а може бути і такою, що рекурсивно-перераховує (тобто не є множиною значень деякої рекурсивної функції).

Виходячи з сказаного, можна запропонувати наступну постановку задачі. На кожному інтервалі часу існування інформаційної бази наявна реалізація функції розстановки у вигляді часткового ефективного оператора Т, n-ку частково-рекурсивних функцій, що є, від n змінних, причому з n рівностей, принаймні m, істинні і, істинні лише у тому випадку, коли визначені і ліва і права частини рівності і вони рівні. Питання про практичну здійсненність доповнюваної інформаційної бази, що модифікується, приймає в цьому випадку наступний вигляд: чи існують ефективні реалізації оператора Т в частотному сенсі? Зрозуміло, що точна реалізація оператора Т зовсім не зобов’язана бути ефективною. З іншого боку, очевидно, що кожна скінчена сукупність об’єктів бази даних (тобто після кожного акту поповнення) рекурсивно-перечислима, але не обов’язково тим же способом, що і після попереднього поповнення.

Приведене формулювання відповідає постановці задачі про частотне рішення проблеми входження в множину, що рекурсивно-перераховує, запропоноване в [25] і що має позитивне вирішення при сформульованому обмеженні – допущенні деякого рівня помилок. Отже, проблема формально вирішувана.

Отже, формально можлива побудова абстрактних конструкцій, що реалізують необчислювані в звичному сенсі об’єкти {94. Цей матеріал викладається на основі нашої роботи [4], написаної ще в кінці 70-х років і опублікованої в 1982 р. Сьогодні все більше учених починають говорити про “необчислювану суть” саме в тій спрямованості, яка і викладена у вказаній роботі.}. Далі, не входячи в подробиці теорії частотних обчислень, сформулюємо лише остаточний результат щодо меж складності формальних конструкцій, що реалізують об’єкти, які цікавлять нас.

1. Для формальної конструкції S і бажаної післяумови R назвемо найслабшою передумовою таку передумову , щоS, розпочинаючи роботу в , закінчить роботу в стані, що задовольняєR, S; при початковому стані, не задовольняючому R, S завершує роботу в не передбачуваному стані, зокрема може не прийти до завершення (зациклюється).

2. Найслабшою вільною передумовою назвемо таку передумову, починаючи роботу в якій,S завершує роботу одним з перерахованих нижче способів. При цьому для кожного з варіантів завершення існує наступна характеризація множини початкових станів:

a) =

тобто S приходить до істинності R;

b)

тобто S приходить до істинності

c) =

тобто S не приходить до правильного завершення;

d)

тобто S приходить до завершення, але за початковим станом не можна визначити, чи буде завершення задовольняти R;

e) &

тобто якщо система прийде до скінченого стану, то він задовольняє R, проте завершимість не гарантується початковим станом;

f)

тобто якщо система прийде до скінченого стану, то він задовольняє , завершимість не гарантується початковим станом;

g)

тобто за початковим станом не можна визначити, чи завершиться робота S, а при завершенні – чи задовольнятиметься R або .

Таким чином , гарантує лише, що система не завершить роботу з “неправильною відповіддю”, причому не виключається можливість не завершення роботи при запуску з.

3. Якщо конструкція S може мати виходом n умов , то

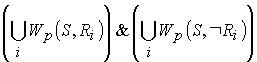
є опис скінченого автомата, представляючого (моделюючого) S.

Скориставшись приведеною термінологією, вкажемо:

• якщо гранично обчислюване в частотному сенсі, то апроксимація такої конструкції може бути побудована за скінченне число кроків. Інакше кажучи, поведінка будь-якої сукупності конструкцій такого роду не може бути складнішою, ніж поведінка контекстно-вільного об’єкта;

• якщо 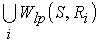гранично обчислюване в частотному сенсі, то апроксимація S може бути побудована за скінченне число кроків, проте оцінка числа кроків невичислима.

Таким чином, можлива реалізація скінченних програм (структур), що моделюють в частотному сенсі нерекурсивні об’єкти, і існують дві межі складності формальної конструкції: нижня межа, при якій поведінка конструкції тривіальна і така, що зводиться до контекстно-вільної моделі, верхня межа - поведінка незводима до скінченої моделі, але скінченно-модельована в частотному сенсі.