
- •Содержание
- •Введение
- •Изображение куба
- •I этап. Определение линии горизонта и точки зрения. Компоновка изображения на плоскости листа.
- •II этап. Линейно-конструктивный рисунок куба в перспективе.
- •I этап. Определение линии горизонта и точки зрения. Компоновка изображения на плоскости листа.
- •II этап. Линейно-конструктивный рисунок куба в перспективе.
- •I этап. Определение линии горизонта и точки зрения. Компоновка изображения на плоскости листа.
- •II этап. Линейно-конструктивное изображение куба в перспективе.
- •Изображение четырехгранной призмы
- •I этап. Определение линии горизонта и точки зрения. Компоновка изображения на плоскости листа.
- •II этап. Линейно-конструктивный рисунок четырехгранной призмы в перспективе.
- •I этап. Определение линии горизонта и точки зрения. Компоновка изображения на плоскости листа бумаги.
- •II этап. Линейно-конструктивный рисунок четырехгранной призмы в перспективе.
- •Изображение окружности в перспективе
- •Изображение конуса
- •I этап. Определение линии горизонта и точки зрения. Компоновка изображения на плоскости листа бумаги.
- •II этап. Линейно-конструктивное построение конуса в перспективе.
- •I этап. Определение линии горизонта и точки зрения. Компоновка изображения на плоскости листа бумаги.
- •II этап. Линейно-конструктивное построение конуса в перспективе.
- •Изображение пирамиды
- •I этап. Определение линии горизонта и точки зрения. Компоновка изображения на плоскости листа.
- •II этап. Линейно-конструктивный рисунок пирамиды в перспективе.
- •I этап. Определение линии горизонта и точки зрения. Компоновка изображения на плоскости листа.
- •II этап. Линейно-конструктивный рисунок пирамиды в перспективе.
- •Изображение цилиндра
- •I этап. Определение линии горизонта и точки зрения. Компоновка изображения на плоскости листа.
- •II этап. Линейно-конструктивный рисунок цилиндра в перспективе.
- •I этап. Определение линии горизонта и точки зрения. Компоновка изображения на плоскости листа.
- •II этап. Линейно-конструктивный рисунок цилиндра в перспективе.
- •Иображение многогранных призм
- •I этап. Определение линии горизонта и точки зрения. Компоновка изображения на плоскости листа.
- •II этап. Линейно-конструктивное изображение шестигранной призмы в перспективе.
- •I этап. Определение линии горизонта и точки зрения. Компоновка изображения на плоскости листа.
- •II этап. Линейно-конструктивный рисунок призмы в перспективе.
- •Изображение шара
- •I этап. Определение линии горизонта и точки зрения. Компоновка изображения на плоскости листа.
- •II этап. Линейно-конструктивный рисунок шара в перспективе.
- •Литература
I этап. Определение линии горизонта и точки зрения. Компоновка изображения на плоскости листа бумаги.
Необходимо определить основные характерные особенности данного геометрического тела, понять трехмерную величину предмета и мысленно представить его изображение на двухмерной плоскости листа бумаги. Следует помнить то, что форма предмета меняется в зависимости от того, с какой точки зрения на него смотреть.
II этап. Линейно-конструктивный рисунок четырехгранной призмы в перспективе.
При построении четырехгранной призмы в перспективе следует помнить, что основаниями такой призмы являются квадраты. Боковыми гранями – одинаковые по размеру прямоугольники. Соотношение между основаниями и боковыми гранями четырехгранной призмы определяет ее пропорции. Рисуя призму в вертикальном или горизонтальном положении можно вести работу по принципу построения куба, а затем удлинить его ребра по вертикали или горизонтали, найдя пропорциональные отношения граней и ребер призмы. Определяя размеры горизонтально расположенной призмы, необходимо помнить о сокращении отрезков, лежащих на горизонтальной прямой.
Для проверки перспективного построения четырехгранной призмы в основании ее плоскости (прямоугольника или квадрата) проводят диагонали. Из точки их пересечения подымают вверх вертикальную линию – центральную ось призмы. Затем проводят диагонали в верхней плоскости грани призмы. Точка их пересечения должна располагаться на центральной вертикальной оси призмы. Перспективное построение вертикальных граней призмы проверяется так же способом проведения диагоналей. Линия, соединяющая точки пересечения диагоналей должна идти в одном перспективном направлении с горизонтальными ребрами призмы.
Для изображения видимых поверхностей формы призмы (контурные линии) толщина линии усиливается, а поверхности, невидимые в натуре выполняются более тонкой линией. Элементы формы первого плана изображения выполняются плотной, выразительной линией, а элементы, уходящие в даль – линией, более тонкой и слабой.
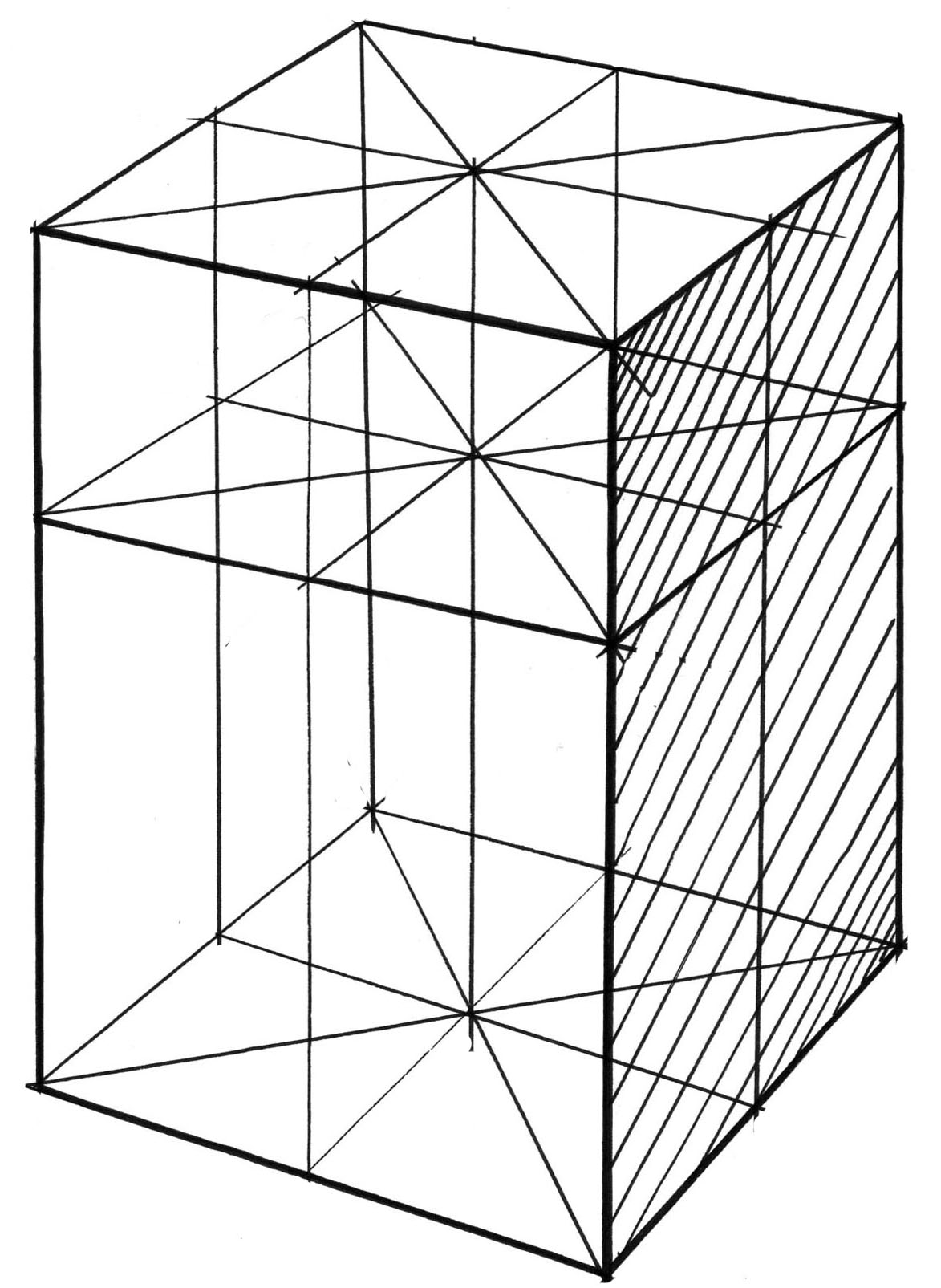
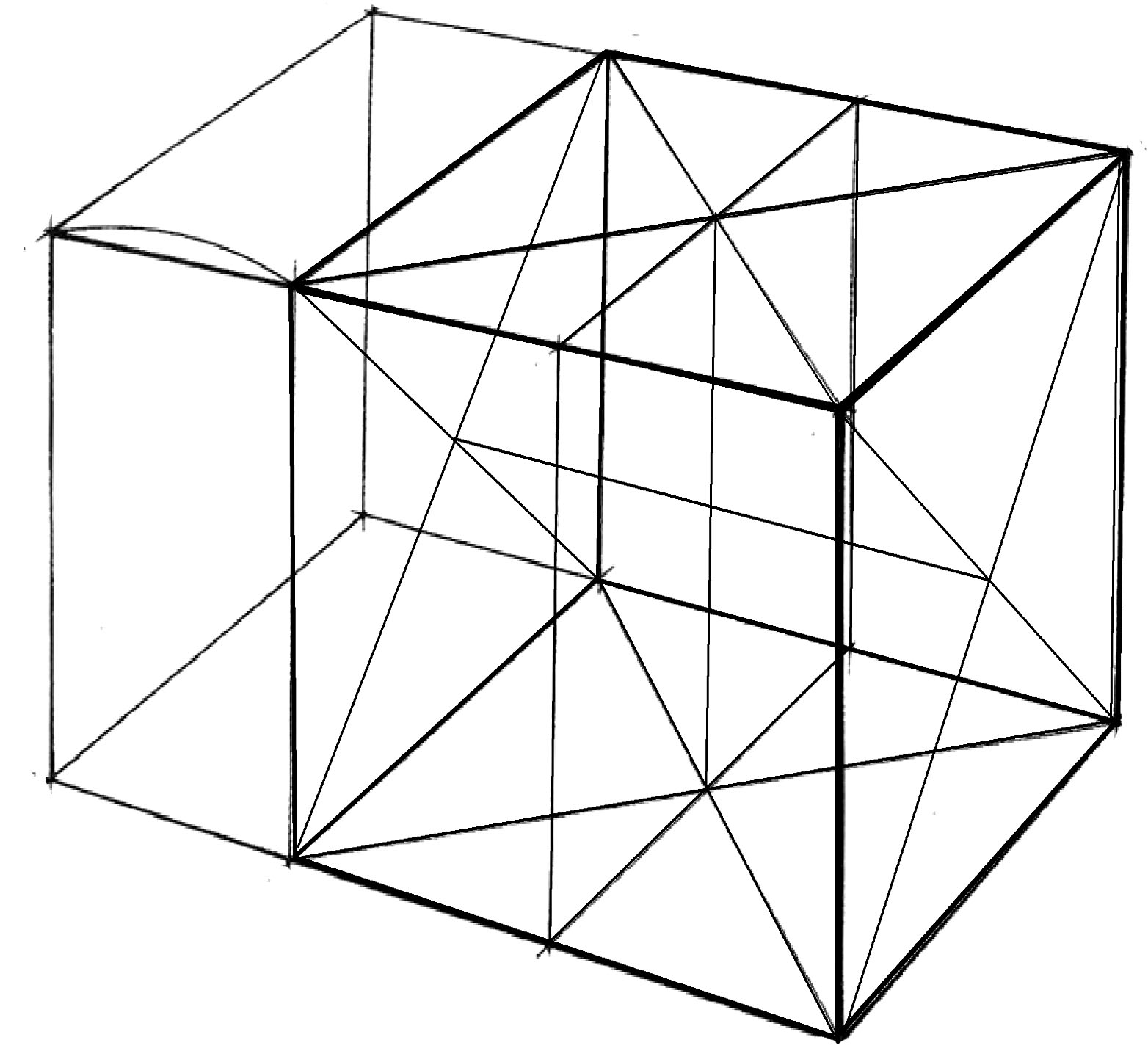
Рис. 10. Линейно- конструктивный рисунок четырехгранной призмы по представлению в горизонтальном и вертикальном положении.
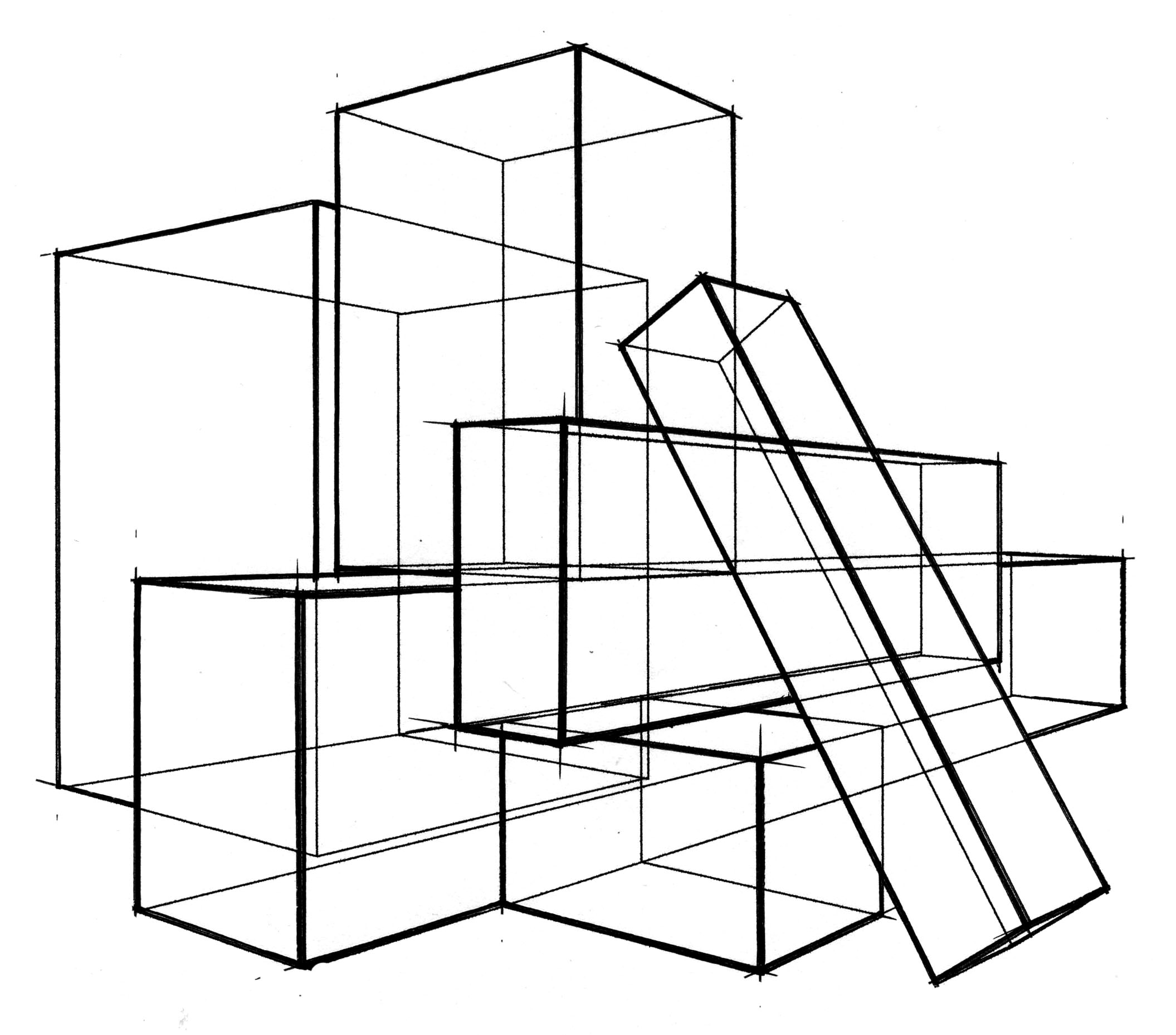
Рис. 11. Композиция из линейно-конструктивных изображений призм
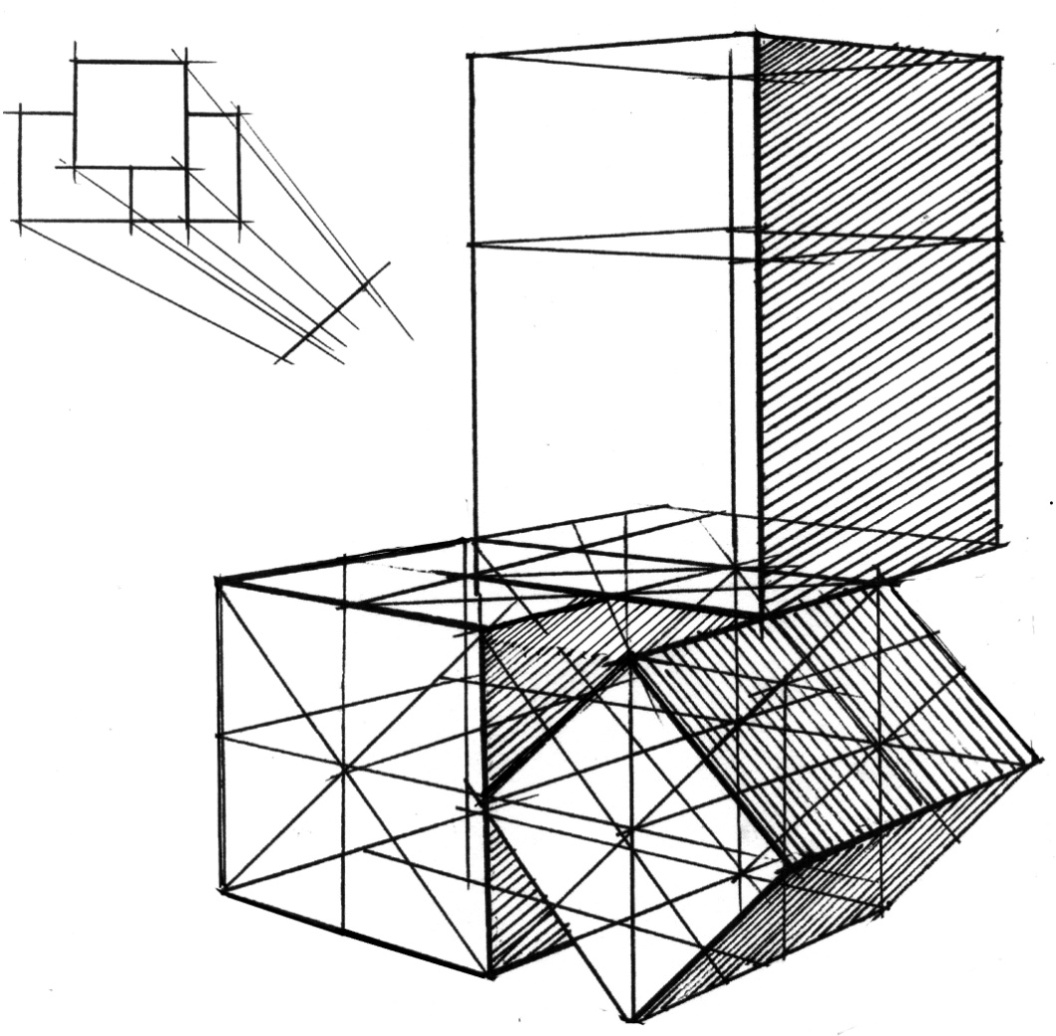
Рис.12. Композиция из линейно-конструктивных изображений призм.
Изображение окружности в перспективе
Цель: Изучение перспективных и конструктивных закономерностей изображения окружности в перспективе.
Задачи:
изучить схемы и способы изображения окружности в перспективе;
передать форму, конструкцию и пропорции окружности в перспективе;
приобрести навыки и умения изображения окружности по памяти и по представлению;
Материалы: бумага (формат А 4, А 3), карандаш, резинка.
Задание №1 Линейно-конструктивный рисунок окружности в перспективе
Методические рекомендации к выполнению задания:
Наибольшую трудность при рисовании конуса или цилиндра тел вращения, представляет изображение круглых оснований, поэтому необходимо вначале познакомиться с перспективой горизонтально и вертикально расположенной окружности.
Окружность в перспективе изображается как эллипс (рис.). Эллипс – это такая замкнутая овальная линия, которая строится на двух взаимно перпендикулярных осях. Две оси эллипса – большая и малая – всегда перпендикулярные прямые и пересекаются в центре эллипса. Отношение малой оси эллипса к большой называется раскрытием эллипса. Эллипс является нециркульной кривой в отличие от овала, применяемого для изображения окружности в аксонометрических проекциях.
Рисунок эллипса следует начинать с изображения его осей. Для окружности, лежащей в горизонтальной плоскости, большая ось эллипса будет всегда горизонтальной прямой, малая – вертикальной. От центра эллипса нужно отложить равные расстояния по большой оси, их сумма определяет размер диаметра окружности. На малой оси откладывается отрезок, который определяет раскрытие окружности в перспективном сокращении в соответствии с пропорциональным соотношением к размеру большего диаметра окружности (максимальной ширины по горизонтали). При этом следует помнить, что центр эллипса и центр окружности – две разные точки. Диаметр окружности, являющийся малой осью эллипса, делится точкой центра окружности на два разных по величине отрезка: ближний к зрителю – больше дальний – меньше (по закону перспективного сокращения), а точка центра окружности по горизонтали делит диаметр – большую ось эллипса – ровно пополам. Следует обратить внимание, что даже самые узкие эллипсы не имеют изломов на концах большой оси. Поэтому при изображении окружности в перспективе, нельзя ограничиваться дугами двух окружностей различных радиусов.
На рис. 16 изображен в перспективе ряд горизонтально расположенных окружностей. Изображение в перспективе окружности имеют вид замкнутых овальных линий. Проследив за их формой, увидим, что по мере приближения к горизонту их малая ось уменьшается и окружность, совпадающая с линией горизонта, изображается в виде прямой горизонтальной линии. По мере возвышения над линией горизонта, видимые замкнутые овалы приближаются по форме к окружности.
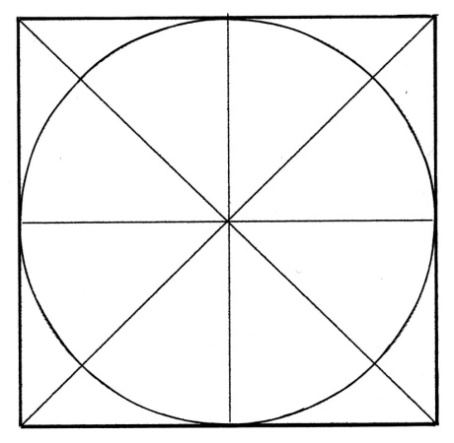
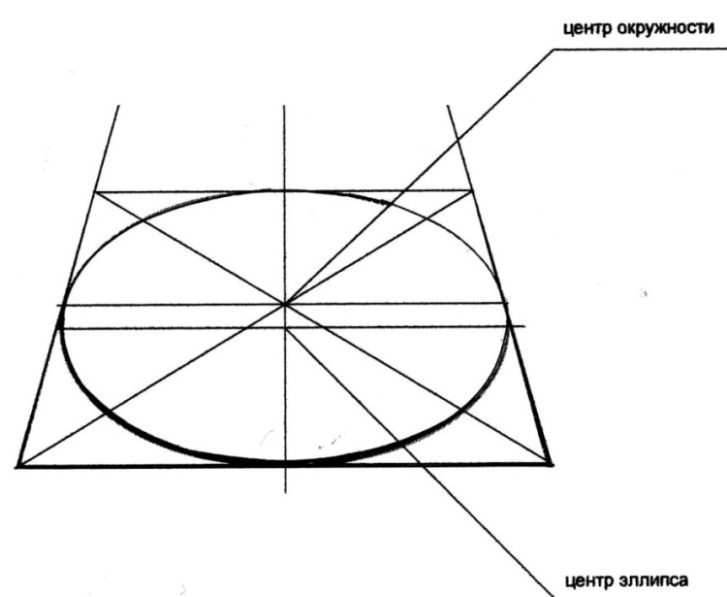
Рис. 13. Изображение квадрата
описанного вокруг окружности Рис. 14. Изображение квадрата описанного вокруг окружности в перспективе
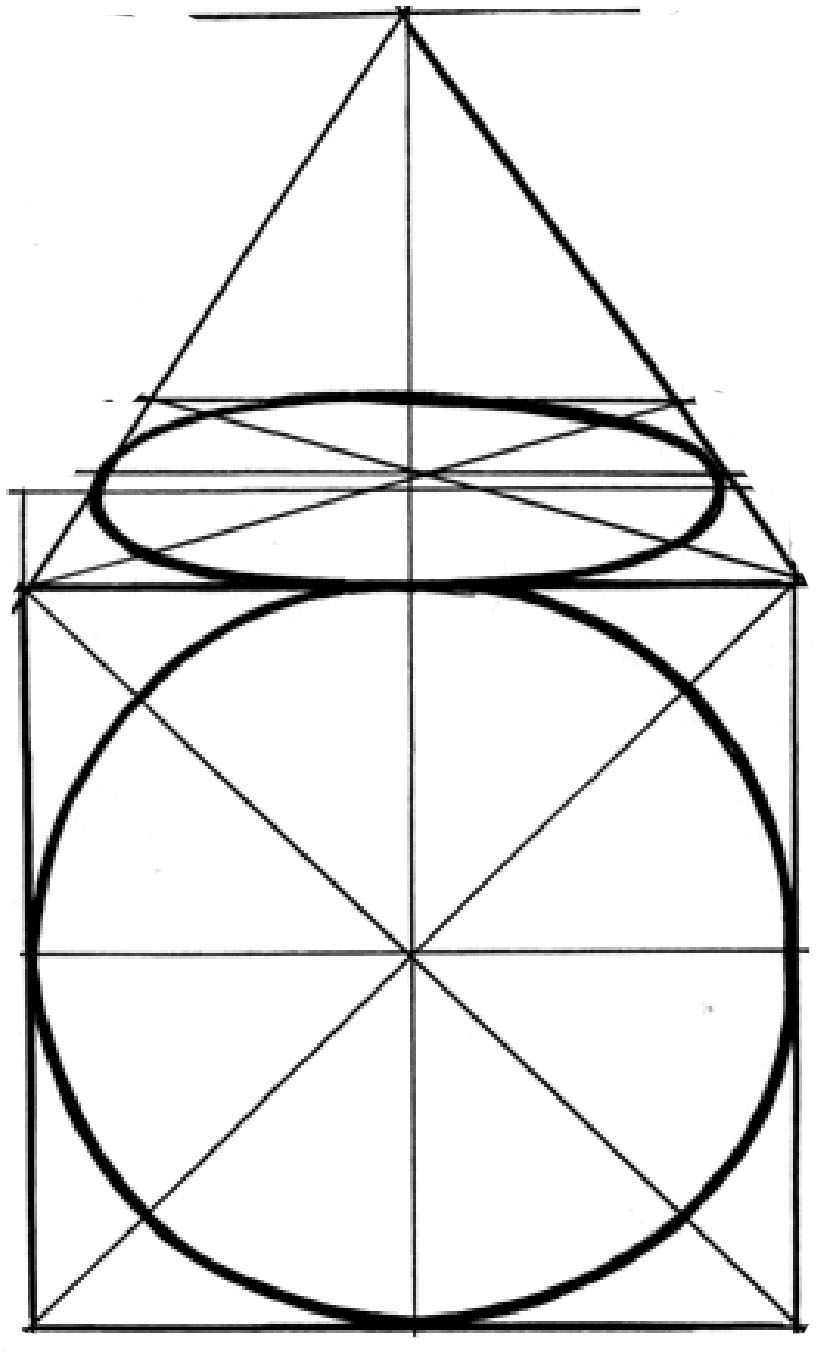
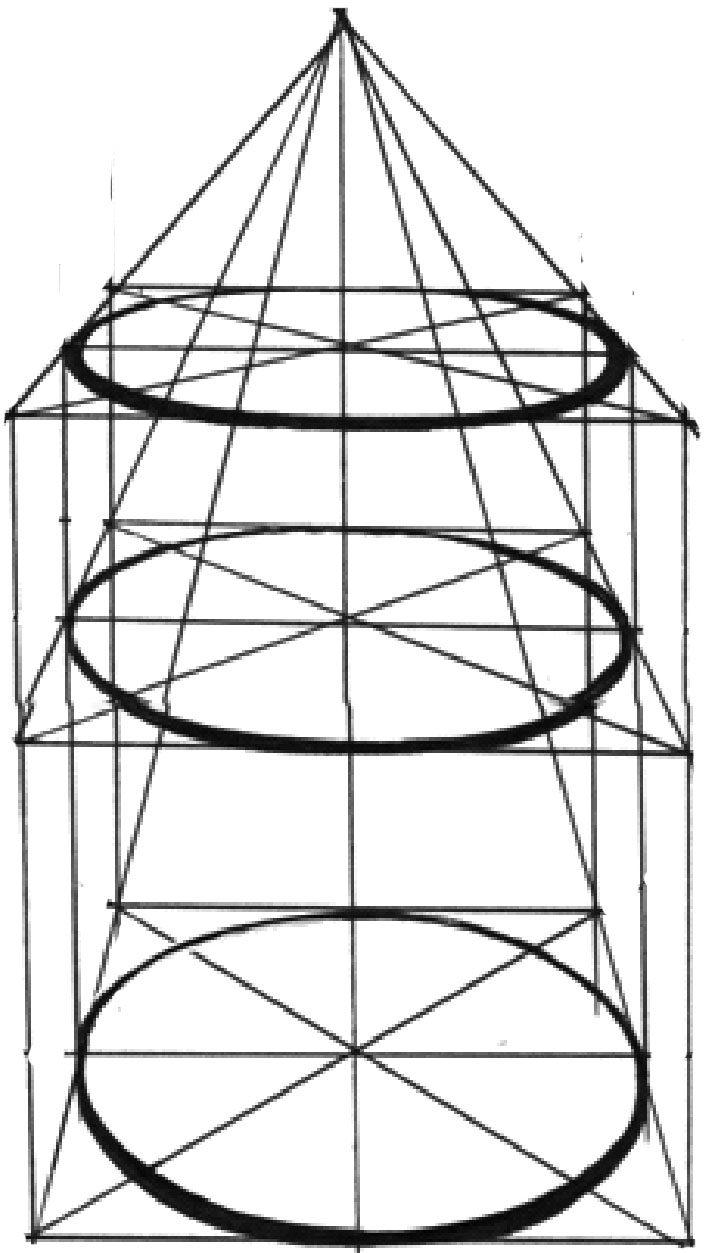
Рис. 15. Перспективное изображение Рис. 16. Перспективное сокращение окружности
окружности относительно линии горизонта
Задание №2. Построить окружность в перспективе способом вписывания ее в квадрат.
Методические рекомендации к выполнению задания:
Для изображения окружности в квадрате необходимо, прежде всего, правильно построить в перспективе квадрат, который находится в горизонтальном или вертикальном положении. Затем определить пропорциональное соотношение его образующих элементов. Найти положение осей и точки, задающие его размеры. При выполнении данного задания нужно учесть следующее:
окружность, вписанная в квадрат, в перспективе имеет форму эллипса.
квадрат и вписанный в него эллипс имеют общий центр – точку пересечения диагоналей квадрата;
кривая эллипса касается сторон квадрата, а точки касания делят стороны квадрата пополам.
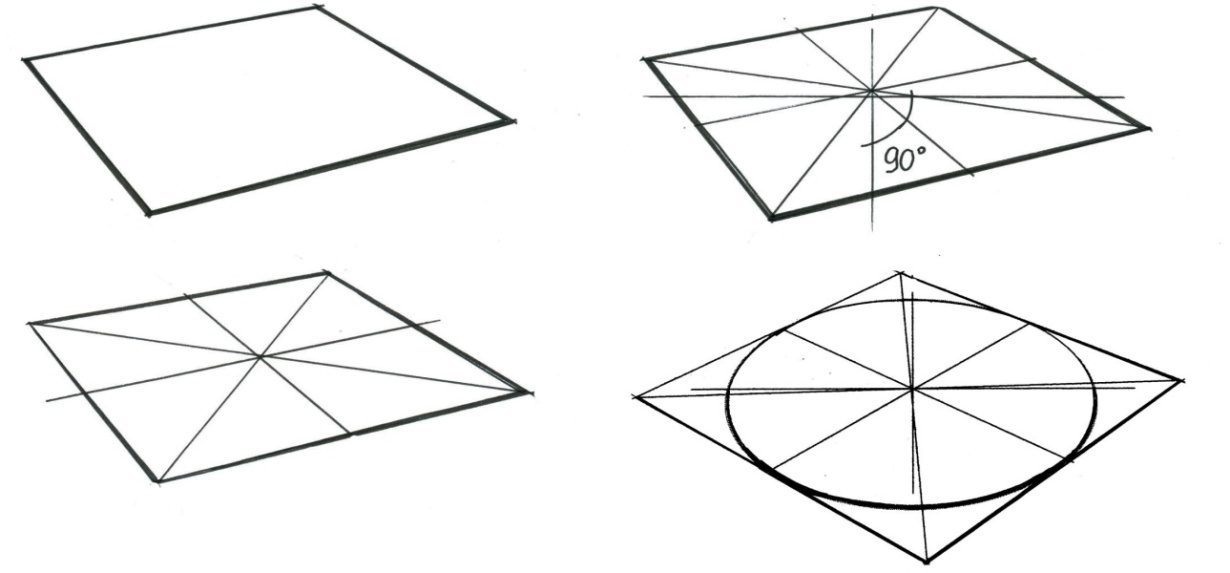
Рис. 17. Этапы построения изображения окружности в перспективе в горизонтальной плоскости способом вписывания ее в квадрат.
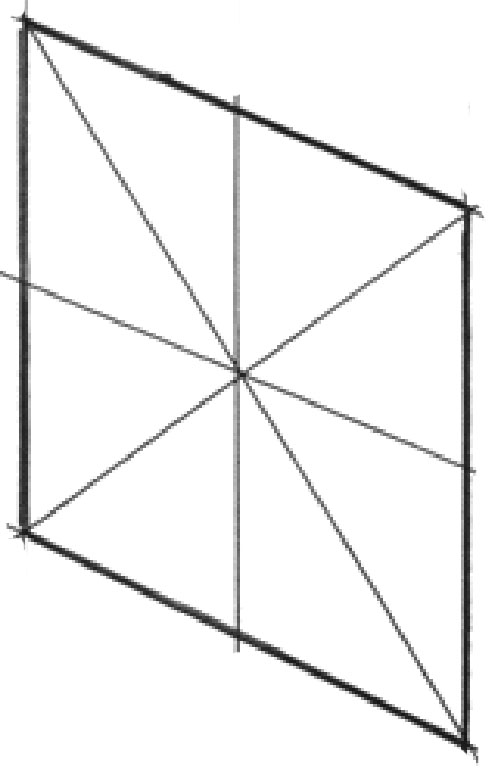
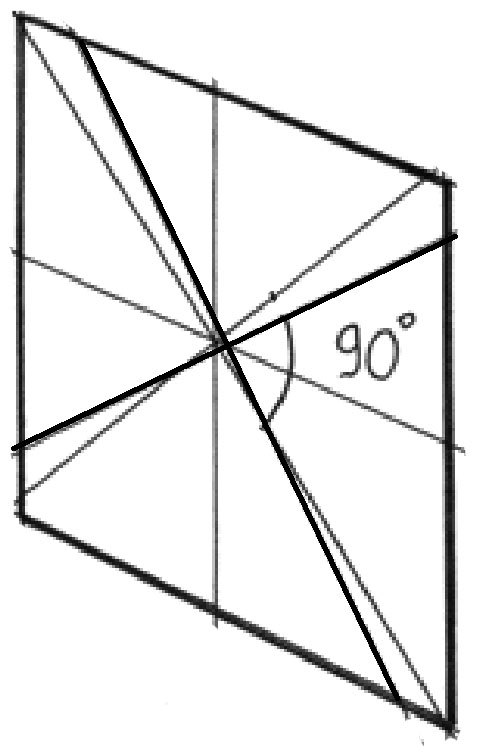
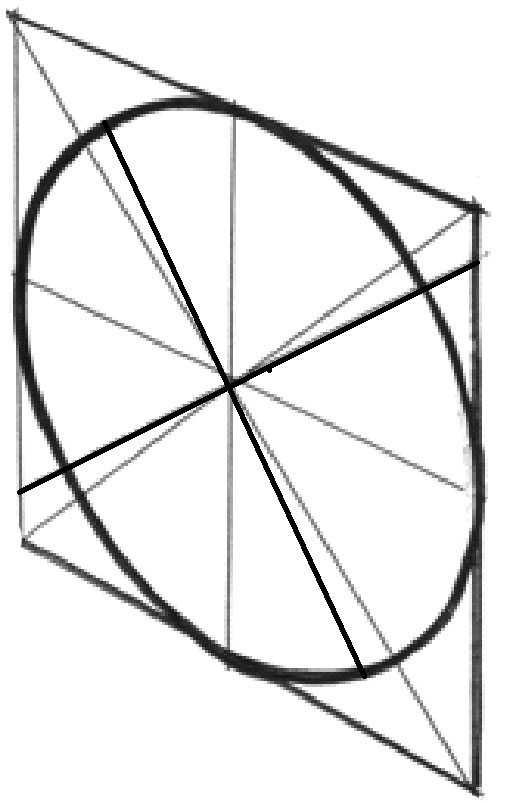
Рис. 18. Этапы построения изображения окружности в перспективе в вертикальной плоскости способом вписывания ее в квадрат.
Задание №3. Построить квадрат вокруг окружности в перспективе.
Методические рекомендации к выполнению задания:
Определить расположение эллипса относительно линии горизонта. Наметить пропорциональное соотношение малой и большой оси эллипса. Построить эллипс на основе взаимно перпендикулярных осей. При этом следует помнить, что малая ось эллипса делится точкой центра окружности на два разных по величине отрезка: ближний – больше, а дальний – меньше (по закону перспективного сокращения), а большая ось эллипса – ровно пополам. Из точек схода на горизонте провести прямые, касательные к эллипсу. Во фронтальной перспективе две стороны квадрата будут параллельны линии горизонта. Затем следует соединить вершины квадрата диагоналями. Точка пересечения диагоналей квадрата должна совпадать с точкой пересечения осей эллипса.
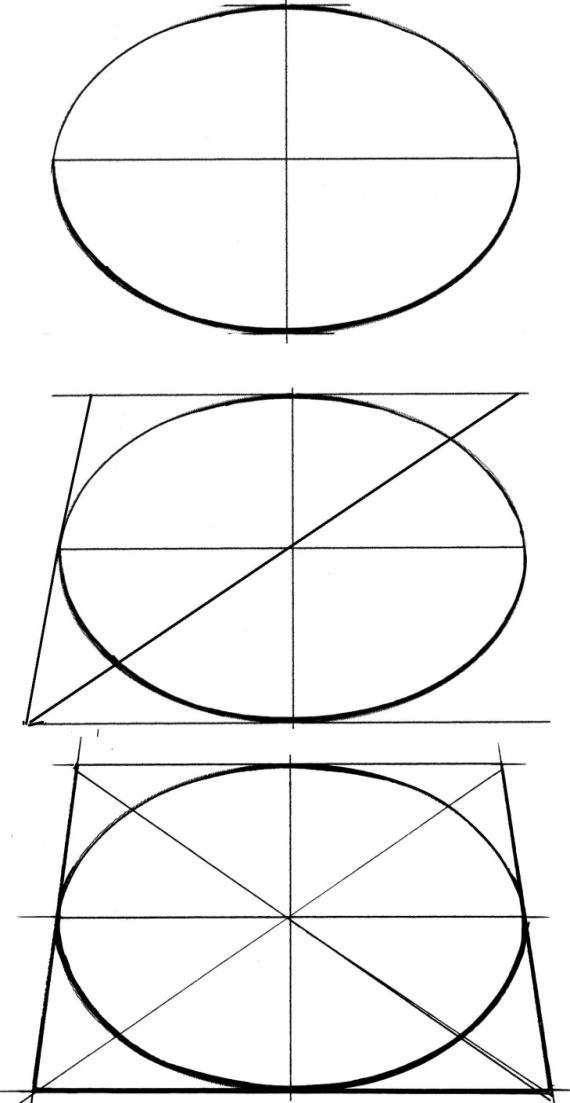
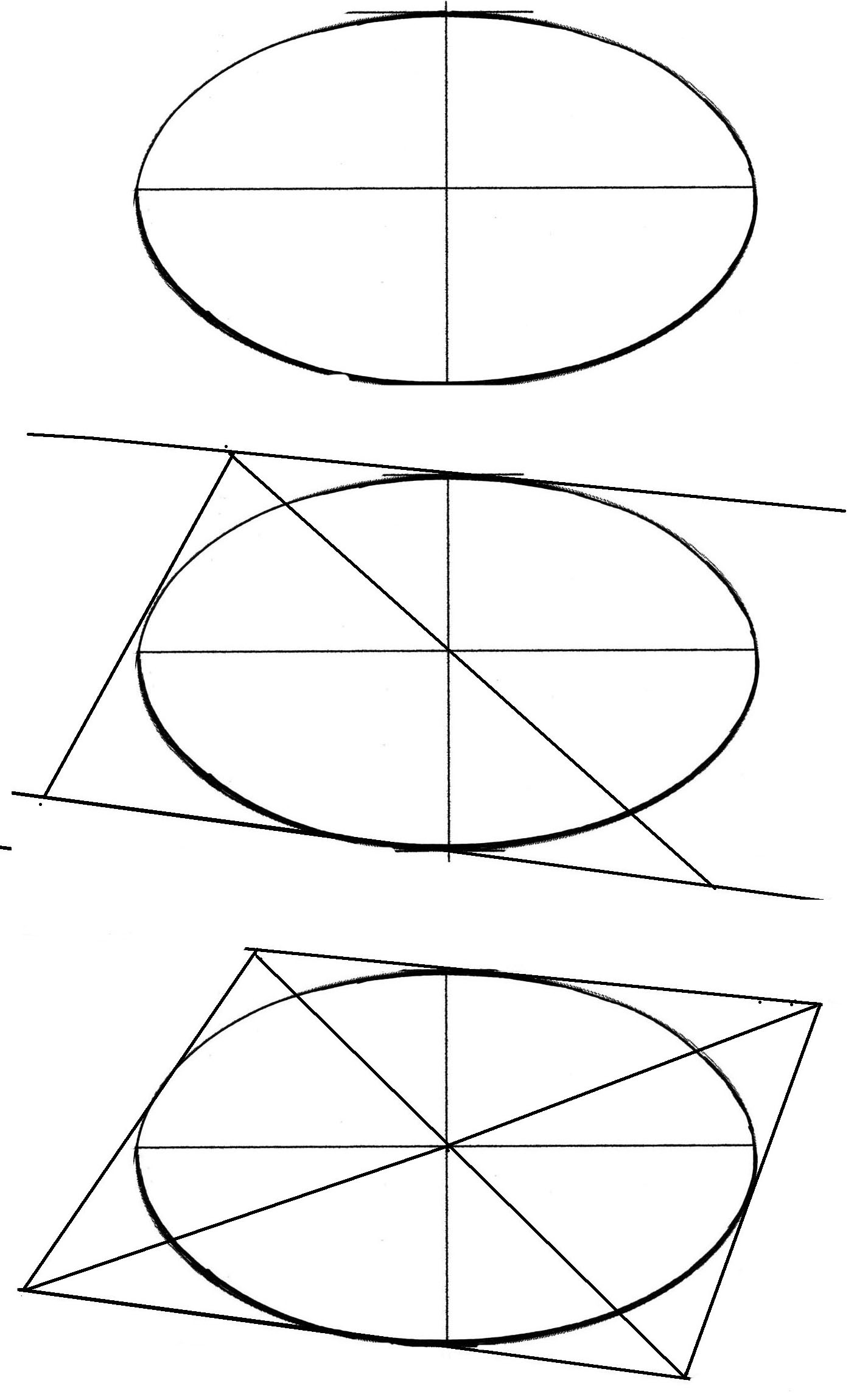
Рис. 19. Последовательность построения изображения квадрата вокруг окружности в перспективе в горизонтальной плоскости.
