К теме 2.7. Гипотезы прочности и их применение

1. Чем характеризуется общее напряженное состояние в любой точке деформируе-

мого тела?

2. Какие площадки и напряжения называются главными?

3. Как обозначается главное напряжение?

4. Что такое гипотезы прочности и каково их назначение?

5. Что такое эквивалентное напряжение?

6. Каковы условия прочности по гипотезам наибольших касательных напряжений и

потенциальной энергии формоизменения?

7. Как производится расчет валов на прочность при совместном действии изгиба и

кручения?

8. Как определяется суммарный изгибающий момент и эквивалентный момент?

К теме 2.8. Устойчивость сжатых стержней

1. Что называется продольным изгибом?

2. Что называется критической силой?

3. Какова формула Эйлера для критической силы при различных случаях закрепле-

ния стержня?

4. Каковы пределы применимости формулы Эйлера?

5. Как производится проверочный расчет сжатого стержня на устойчивость?

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ

КОНТРОЛЬНОЙ РАБОТЫ № 1

В рекомендованных учебниках [1], [2], [3] учащиеся найдут достаточное число примеров задач подобных тем, которые включены в контрольную работу. Поэтому ниже даны краткие методические указания для решения задач контрольных работ.

Первую задачу необходимо решать после изучения темы 1.1.2.1. В задачах этого типа рассматривается равновесие плоской системы сходящихся сил и требуется определить реакции двух шарнирно соединенных между собой стержней, удерживающих два груза. Таким образом к шарниру В, в каждой задаче приложены четыре силы, из которых две неизвестны.

Существует три метода решения задач:

1. аналитический;

2. графоаналитический;

3. графический.

Для задач этого типа универсальным методом является аналитический.

Алгоритм решения задач на равновесие:

1. Выделяют объект равновесия, т.е. тело или точку, равновесие которых в данной

задаче следует рассмотреть.

2. К выделенному объекту равновесия прикладывают заданные силы.

3. Выделенную точку или тело освобождают от связей и вместо них прикладывают

реакции связей (аксиома 6).

4. Выбирают координатные оси и составляют уравнения равновесия, используя условия равновесия системы сходящихся сил на плоскости ΣFix = 0; ΣFiу = 0

5. Решают составленные уравнения и определяют реакции стержней.

1. Найденные неизвестные величины проверяют с помощью уравнений равновесия,

не использованных при их определении, либо решить задачу графически.

Пример 1. К кронштейну АБС в точке В подвешены два груза F₁=3кН, F₂=1кН, как указано на схеме 1. Стержень кронштейна АВ образует с вертикальной стенкой угол α= 30⁰, стержень ВС – угол β= 60⁰. Пренебрегая трением на блоке Д, определить усилия в стержнях АВ и ВС.

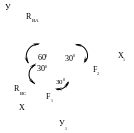
Выделяем в качестве объекта равновесия узел В. Прикладываем к нему заданные силы F, F₂. При этом сила F₂ будет приложена к узлу В горизонтально, так как передается через неподвижный блок Д, который изменяет направление силы, но не влияет на ее величину. Освободим узел В от связей, т.е. отбросим стержни АВ и ВС и приложим их реакции R_ВА, R_ВС. Эти реакции направлены от узла В, как показано на рисунке 1.б., это соответствует предположению, что оба стержня АВ и ВС растянуты. Выбираем координатные оси таким образом, чтобы одна из них прошла по реакции. Находим углы наклона сил к осям х и у.

Составляем уравнения равновесия для плоской системы сходящихся сил:

ΣFix = 0;

R_ВС + F₁ cos 60⁰ – F₂ cos 30⁰ = 0;

ΣFiу = 0;

R_ВА - F₁ cos 30⁰ – F₂ cos 60⁰ = 0

Решаем полученную систему уравнений:

R_ВС = -F₁ cos 60⁰ +F₂ cos 30⁰ = -3·0,5 + 1·0,867 = - 0,633 кН

Знак минус перед численным значением реакции R_ВС показывает, что стержень ВС в действительности не растянут, а сжат.

Из второго уравнения определяем:

R_ВА = F₁ cos 30⁰ + F₂ cos 60⁰ = 3·0,867 + 1·0,5 = 3,1 кН

Знак плюс перед численным значением показывает что стержень 1, как и предполагалось, растянут силой R_ВА = 3,1 кН

Решение задачи следует обязательно проверять. Лучшим способом проверки может быть либо решение с использованием иных координатных осей, либо решение другим методом, например графическим.

Выбираем оси координат х₁ и у₁ и составляем уравнение на любую из осей координат.

ΣFix₁ = 0;

F₂ - R_ВА cos 60⁰ - R_ВС cos 30⁰ = 0;

1 – 3,1·0,5 – (-0,633) ·0,867 = 0;

1 – 1,55 + 0,55 = 0;

0 = 0

Вторую задачу следует решать после изучения темы 1.1.2.2.

Во всех задачах требуется определить реакции опор балок. Учащимся необходимо приобрести навыки определения реакций опор, так как с этого начинается решение задач по сопротивлению материалов и деталям машин.

Алгоритм решения задачи:

1. Изобразить балку вместе с нагрузками;

2. Выбрать расположение координатных осей, совместив ось Х с балкой, а ось У

направив перпендикулярно оси Х;

3. Произвести необходимые преобразования заданных активных сил: равномерно

распределенную нагрузку по закону прямоугольника – ее равнодействующей, приложенной в середине участка распределения нагрузки;

4. Освободить балку от опор, заменив их действие реакциями опор, направленными

вдоль выбранных осей координат.

5. Составить уравнения равновесия статики таким образом и в такой последова-

тельности, чтобы решением каждого из этих уравнений было определение одной из неизвестных реакций опор;

6. Проверить правильность найденных опорных реакций по уравнению, которое не

было использовано для решения задачи.

Пример 2. Определить реакции опор балки.

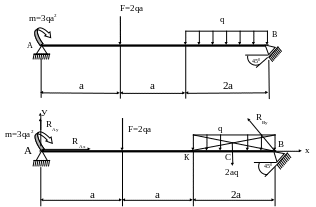
1. Изображаем балку с действующими на нее нагрузками.

2. Изображаем оси координат.

3. Равнодействующая 2аq равномерно распределенной нагрузки, приложенная в

точке пересечения диагоналей прямоугольника (рис. 2а), переносится по линии своего действия в середину участка КВ, в точку С.

4. Отбрасываем опорные закрепления и заменяем их действия реакциями (рис. 2б).

5. Составляем уравнения статики и определяем неизвестные реакции опор.

ΣMa=0;

m+Fa+2a·3a·q-R_By·4a·cos45⁰=0;

R_By=(m+Fa+2a·3a·q) / 4a·cos45⁰=(3qa²+2q·a²+6q·a²) / 4a·0,7071=3,89qa

ΣMв=0;

m+R_Ay·4a-F·3a-2aq·a=0;

R_Ay=(-m+F·3a+2a²q)/4a=(-3qa²+2qa·3a+2a²q)/4a=1,25qa;

ΣF_ix=0;

R_Ax - R_By·cos45⁰=0;

R_Ax=R_By·cos45⁰=3,89qa·0,7071=2,75qa

6. Проверка

ΣF_iу=0;

R_Ay-F-q·2a+R_By·cos45⁰=0;

1,25qa-2qa-2qa+3,89qa·0,7071=0;

0=0

Третью задачу следует решать после изучения темы 1.1.2.2.

Алгоритм решения задачи:

1. Изобразить на рисунке тело, равновесие которого рассматривается, с действую-

щими на него активными и реактивными силами и выбрать систему координат.

2. Определить значения сил F₂, Fr₂;

3. Составить шесть уравнений равновесия.

4. Решить уравнения и определить реакции опор.

Пример 3. На вал (рис. 3а) жестко насажены шкив 1 и колесо 2.

Определить силы F₂, Fr₂=0,4 F₂, а так же реакции опор А и В, если F₁=100Н.

1. Изображаем вал со всеми действующими на него силами и выбираем оси коор-

динат (рис. 3б). Схемы (2а, б).

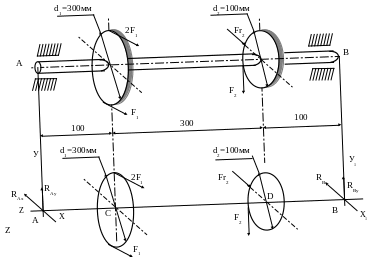
2. Определяем F₂ и Fr₂ из условия равновесия тела, имеющего неподвижную ось: (F₁·d₁ /2) - (F₂·d₂ /2) = 0;

F₂=F₁·d₁/d₂;

F₂=F₁·d₁/0,1=100·0,3/0,1=300H

Fr₂=0,4F₂=0,4·300=120Н

3. Составляем шесть уравнений равновесия

ΣМ_ix=0;

-R_By ·АВ + F₂·АВ=0; (1)

ΣМ_iу=0;

3F₁·AC+Fr₂·AD-R_Bx·AB=0; (2)

ΣМix₁=0;

R_Ay·AB-F₂·DB=0; (3)

ΣМiу₁=0;

R_Ax·AB-3F₁·CB-Fr₂·DB=0; (4)

ΣF_ix=0;

-R_Ax+3F₁+Fr₂-R_Bx=0; (5)

ΣF_iу=0;

R_Ay-F₂+ R_Bу=0; (6)

4. Решением уравнения (1), (2), (3), (4) и определяем реакции опор.

Из (1):

R_Bу= F₂·AD/АВ=300·0,4/0,5=240Н;

Из (2):

R_Bx=(3F₁·АС+ Fr₂·AD)/АВ=(3·100·0,1+120·0,4)/0,5=156Н;

Из (3):

R_Ay= F₂·DB/АВ=300·0,1/0,5=69Н;

Из (4):

R_Ax=(3F₁·СВ+ Fr₂· DB)/АВ=(3·100·0,4+120·0,1)/0,5=264Н

5. Проверяем правильность найденных реакций опор. Используем уравнение (5).

ΣF_ix=0;

3F₁+ Fr₂- R_Ax-R_Bx=0;

300+120-264-156=0;

0=0

Следовательно, реакции R_Ax и R_Bx определены верно.

Используем уравнение (6):

ΣF_iу=0;

R_Ay-F₂+ R_Bу=0;

60-300+240=0;

0=0

Четвертую задачу следует решать после изучения темы 2.4.

Кручение – это такой вид деформации бруса, при котором в его поперечных сечениях возникает единственный внутренний силовой фактор – крутящий момент обозначенный Т.

Для того, чтобы брус подвергался кручению он должен быть нагружен парами сил, плоскости действия которых перпендикулярны к его продольной оси. Моменты этих пар будем называть скручивающими моментами и обозначать буквой «Те».

Во всех случаях будем считать, что алгебраическая сумма скручивающих моментов равна 0, т.е. брус находится в равновесии. Применяя метод сечений и рассматривая равновесия оставленной части, приходим к выводу, что внутренние системы, возникающие в поперечном сечении бруса должны дать момент (крутящий момент), уравновешивающий внешние моменты, приложенные к оставленной части.

Крутящий момент, возникающий в произвольном поперечном сечении бруса, численно равен алгебраической сумме скручивающих моментов приложенных к оставленной части.

Знак крутящего момента не имеет физического смысла, но для определенности при построении эпюр условимся о следующем правиле знаков.

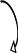
Будем считать крутящий момент положительным, если для наблюдателя, смотрящего на проведенное сечение, он представляется направленным по часовой стрелке и отрицательным против часовой стрелки.

График, показывающий закон изменения крутящих моментов по длине бруса, называется эпюрой крутящих моментов.

Алгоритм решения задачи:

1. Определить значение скручивающих моментов ( подводимого к шкиву 1 и

снимаемых со шкивов 2, 3, 4 ) если они не заданы по условию задачи.

2. Построить эпюры крутящих моментов.

3. Определить диаметры каждого участка ступенчатого вала из условия прочно

сти. Окончательно принимаемые значения должны быть округлены до ближайших стандартных по ГОСТ 6636-69.

4. Вычертить в масштабе эскиз ступенчатого вала.

5. Построить эпюру углов поворота сечения относительно левого торца вала.

6. Определить полный угол закручивания.

Пример 4. На ступенчатом валу (рис. 5) жестко закреплены четыре шестерни. Ве-

дущая шестерня сообщает валу вращающий момент Те₁=1200Нм;

Другие шестерни передают вращающие моменты на валы, параллельные первому Те₂ =400Нм; Те₃ =600Нм; Те₄ =200Нм. Требуется построить эпюру крутящих моментов ступеней вала и полный угол закручивания с построением эпюры углов поворота сечений относительно левого торца вала. Допускаемое напряжение

τ_adm=32 МПа; ℓ₁=120мм; ℓ₂=180мм; ℓ₃=100мм; G=8·10¹⁰Па.

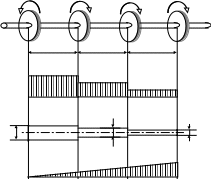
Те₁ Те₂ Те₃ Те₄

ℓ₁ ℓ₂ ℓ₃

1200 800

200

Эп. «Т»(Нм)

^{0 0}

d₂ d₃

d₁

0,196

Эп. «φ» (град) 0,081

0,293

Поскольку скручивающие моменты по условию задачи заданы, строим эпюру крутящих моментов.

1. Для построения эпюры крутящих моментов определяем величины крутящих

моментов на каждом участке вала. Для этого воспользуемся правилом: крутящий момент в любом сечении вала численно равен алгебраической сумме внешних скручивающих моментов, действующих по одну сторону от выбранного сечения. Рассмотрим действие внешних моментов слева от сечения.

В сечении 1-1 Т₁ = Те₁ = 1200 Нм;

в сечении 2-2 Т₂ = Те₁ – Те₂ = 1200 – 400 = 800 Нм;

в сечении 3-3 Т₃ = Те₁ – Те₂ – Те₃ = 1200 – 400 – 600 = 200 Нм;

Эпюра крутящих моментов для вала показана на рис. 4.

2. Диаметры вала на каждом их участке определяем по формуле

d ≥ )