Совместные действия изгиба и кручения стержня

На практике деформации кручения часто сопутствует изгиб. Как правило, при работе вал изгибается собственным весом, весом шкивов, давлением на зубья шестерен, натяжением ремней и т.д. Сочетание изгиба с кручением имеет место в пространственных рамах, коленчатых валах и других элементах конструкций.

В предыдущих разделах рассматривались такие частные случаи слож­ного сопротивления (косой изгиб, внецентренное растяжение или сжатие), при которых в поперечных сечениях бруса возникали только нормальные напряжения, и, следовательно, имело место одноосное напряженное состо­яние. Это позволило при выводе расчетных формул использовать сечения произвольной формы.

В случае изгиба с кручением от крутящего момента в поперечных сечениях бруса возникают касательные напряжения, которые рассчитываются по разному для круглых и прямоугольных брусьев. Вследствие этого, рассматривать расчет сечений произвольной формы не представляется возможным.

Кручение с изгибом – частный случай сложного сопротивления, который может рассматриваться как сочетание чистого кручения и поперечного изгиба.

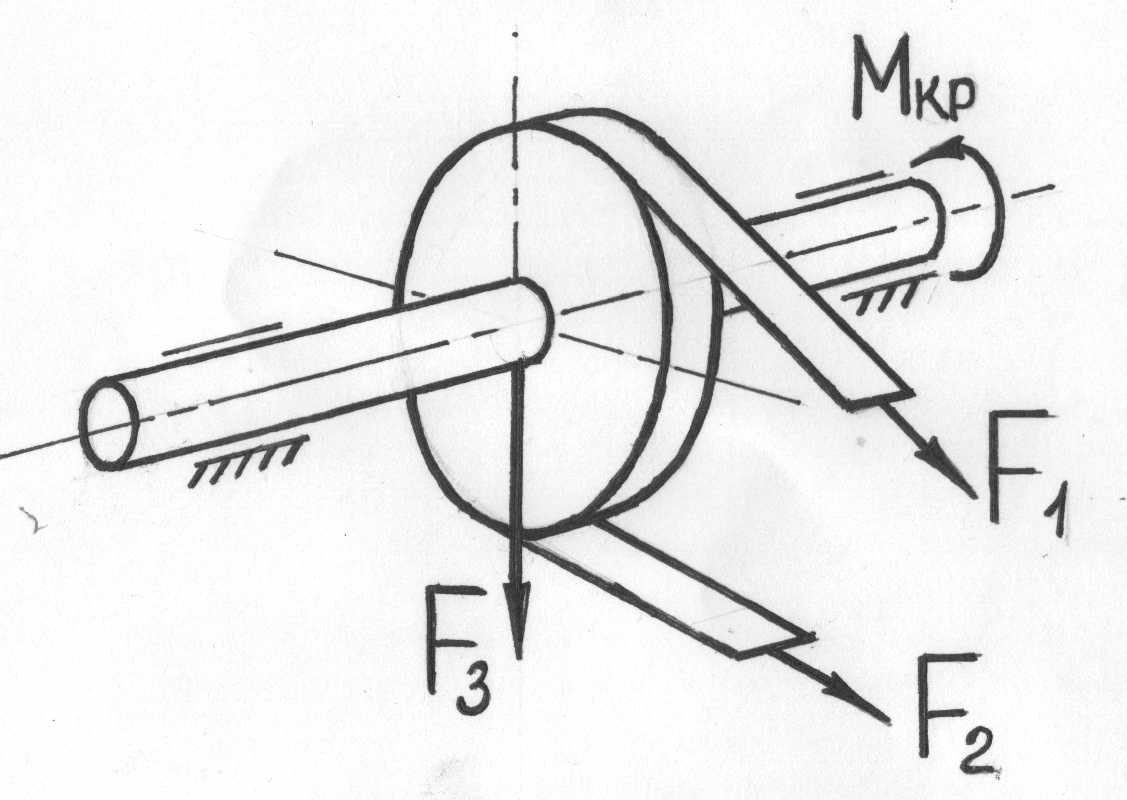
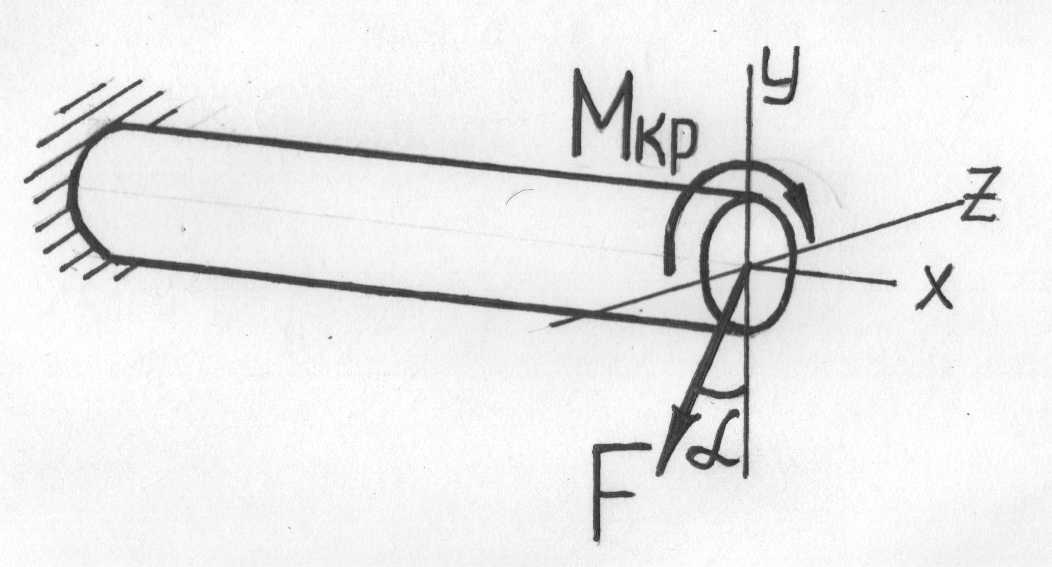
Рис.7.28

Определение внутренних усилий и напряжений при кручении с изгибом

Для определения внутренних усилий воспользуемся методом сечений:

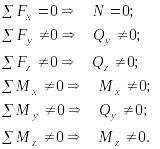
Обычно две составляющие поперечной силы (Q_y, Q_z) и изгибающего момента (M_y, M_z) приводят к их полным результирующим

Заметим, что часто поперечной силой пренебрегают (для достаточно длинных валов) и рассматривают кручение с изгибом как совместное действие крутящего (M_x, M_кр, T) и изгибающего (M_и) моментов.

Расчет валов круглого (кольцевого) поперечного сечения на кручение с изгибом

Исследуем этот вид деформации стержня на примере расчета вала кругового (кольцевого) поперечного сечения на совместное действие изгиба и кручения (рис. 7.29).

Рис.7.29

Примем следующий порядок расчета.

1. Разлагаем все внешние силы на составляющие

P_1x, P_2x,..., P_nx и P_1y, P_2y,..., P_ny.

2. Строим эпюры изгибающих моментов M_ч и M_y. от этих групп сил.

У кругового и кольцевого поперечного сечений все центральные оси главные, поэтому косого изгиба у вала вообще не может быть, следовательно, нет смысла в каждом сечении иметь два изгибающих момента M_x, и M_y, а целесообразно их заменить результирующим (суммарным) изгибающим моментом (рис.7.30)

,

который вызывает прямой изгиб в плоскости его действия относительно нейтральной оси п—п, перпендикулярной вектору М_изг. Эпюра суммарного момента имеет пространственное очертание и поэтому неудобна для построения и анализа. Поскольку все направления у круга с точки зрения прочности равноценны, то обычно эпюру М_изг спрямляют, помещая все ординаты в одну (например, вертикальную) плоскость. Обратим внимание на то, что центральный участок этой эпюры является нелинейным.

Рис.7.30

3. Строится эпюра крутящего момента М_z.. Эпюра крутящих моментов строится так же, как и при чистом кручении.

4. Находится опасное сечение вала.

Опасное сечение вала будем искать, как и прежде, по эпюрам внутренних усилий. При построении эпюр внутренних усилий при кручении с изгибом необходимо иметь ввиду следующие правила:

- эпюры крутящего момента M_x, а также эпюры составляющих поперечной силы Q_y, Q_z и изгибающего момента M_y, M_z строятся по той же процедуре, что и ранее;

- результирующая поперечная сила Q может не лежать в плоскости действия результирующего изгибающего момента M_и, а потому между ними уже не будет соблюдаться зависимость Журавского (dM/dx=Q), а, следовательно, и правила проверки эпюр, введенные для плоского изгиба;

- эпюра полного изгибающего момента будет прямой только на тех участках, где M_y и M_z ограничены прямыми с общей нулевой точкой, на участках, где такая общая точка отсутствует эпюра M_и будет описываться вогнутой кривой и строится по точкам (связано с тем, что вектор M_и в разных сечениях имеет различное направление).

Опасное сечение при кручении с изгибом устанавливается из совместного анализа эпюр крутящего M_x и полного изгибающего M_и моментов. Если в сечении вала постоянного диаметра с наибольшим изгибающим моментом М действует наибольший крутящий момент М_кр, то это сечение является опасным.

Если же такого явного совпадения нет, то опасным может оказаться сечение, в котором ни М ни М_кр не являются наибольшими. Еще больше осложняется задача при валах переменного диаметра; у таких валов наиболее опасным может оказаться такое сечение, в котором действуют значительно меньшие изгибающие и крутящие моменты, чем в других сечениях.

В случаях, когда опасное сечение не может быть установлено непосредственно по эпюрам М и М_кр , необходимо проверить прочность вала в нескольких предположительно опасных сечениях.

5. После установления опасного сечения вала в нем находят опасные точки. В сечении возникают одновременно нормальные напряжения от изгибающего момента и касательные напряжения от крутящего момента и поперечной силы. В валах круглого сечения, длина которых во много раз больше диаметра, величины наибольших касательных напряжений от поперечной силы относительно невелики и при расчете прочности валов на совместное действие изгиба и кручения не учитываются.

Наибольшие напряжения изгиба возникают в точках k и k^/, наиболее удаленных от нейтральной оси (рис. 7.31),

.

где W_изг — момент сопротивления при изгибе.

В этих же точках имеют место и наибольшие касательные напряжения кручения

,

где W_р— момент сопротивления при кручении.

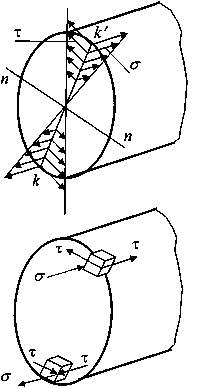Рис.7.31

Как видно из рис. 7.31, в данном случае имеет место плоское напряженное состояние и расчет на прочность должен вестись по одной из гипотез прочности. Для пластичных материалов применяют гипотезу наибольших касательных напряжений (III) или энергетическую гипотезу (IV).

Условие прочности по III гипотезе записывается в виде

. (44)

В рассматриваемом случае

,

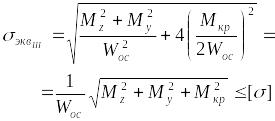или

, (45)

где - эквивалентный момент по третьей гипотезе прочности.

Условие прочности по IV гипотезе прочности записывается в виде

. (46)

В рассматриваемом случае

,

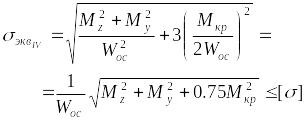или

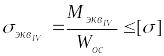, (47)

где - эквивалентный момент по четвертой гипотезе прочности.

Для хрупких материалов может быть использована гипотеза прочности Мора, которая для пластичных материалов приводится к третьей гипотезе, а для очень хрупких – к первой гипотезе

. (48)

Аналогичный расчет проводится и для кольцевого сечения.

Пример 9.

Стальной вал круглого поперечного сечения передает мощность N=14,7 кВт при угловой скорости =10,5 рад/с. Величина наибольшего изгибающего момента, действующего на вал M_и=1,5 кНм. Исходя из условий прочности по III и IV теориям прочности, определить необходимый диаметр вала, если =80 МПа.

Решение.

Условие прочности при одновременном действии изгиба и кручения по III гипотезе прочности

.

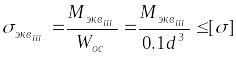Находим величину передаваемого валом крутящего момента

.

Эквивалентный момент по третьей гипотезе прочности равен

а диаметр вала

,

или =63,5 мм.

Условие прочности при одновременном действии изгиба и кручения по IV гипотезе прочности

.

Эквивалентный момент по четвертой гипотезе прочности равен

,

а диаметр вала

,

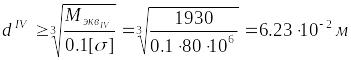или =62,3 мм.

Таким образом, расчет по энергетической теории прочности дал более экономичный размер сечения, чем по критерию наибольших касательных напряжений.

Расчет брусьев прямоугольного сечения на кручение с изгибом

Рассмотрим брус прямоугольного сечения, нагруженный таким образом, что в его поперечных сечениях действуют изгибающие моменты M_z и M_y, а также крутящий момент M_x (рис. 7.32).

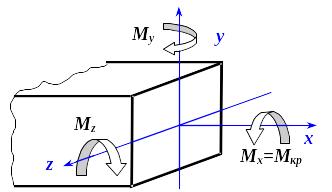
Рис. 7.32

Чтобы проверить прочность бруса, нужно в опасном сечении найти опасную точку, вычислить для нее эквивалентное напряжение (по одной из теорий прочности) и сопоставить его с допускаемым напряжением.

Для нахождения опасной точки сечения построим эпюры напряжений от всех силовых факторов (рис. 7.33).

Эпюры нормальных и касательных напряжений наглядно показывают, что, в отличие от круглого сечения, точки, в которых имеют место максимальные нормальные и максимальные касательные напряжения, не совпадают. В следствие этого, условие прочности составляют, как минимум для трех наиболее опасных точек поперечного сечения.

Опасной точкой по нормальным напряжениям является точка С, в которой от M_y и от M_z положительны, или точка A, в которой от M_y и от M_z также одного знака, но отрицательны. Касательные напряжения от крутящего момента в этих точках равны нулю. Таким образом, в этих точках имеет место линейное напряженное состояние.

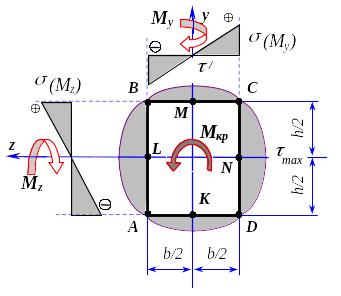
Рис.7.33

Опасной точкой по касательным напряжениям является точка N (или L), лежащая в середине длинной стороны прямоугольника. Кроме того, в этой точке действуют максимальные нормальные напряжения от изгибающего момента M_y.

Следует отметить, что в точке M (или K), расположенной в середине короткой стороны также действуют касательные напряжения (несколько меньшие ) и максимальные нормальные напряжения от M_z.

Таким образом, в точках поперечного сечения N, M, (L, K) имеет место плоское напряженное состояние, которое обуславливает использование гипотез прочности при расчетах на прочность. Для пластичных материалов применяют III (наибольших касательных напряжений) и IV (энергетическую) гипотезы прочности.

Составим условия прочности для трех предположительно опасных точек поперечного сечения

т. C: ; .

т. N: ; , .

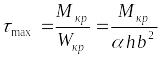т. M: ; , .

Расчетная формула по четвертой гипотезе прочности

.

Для хрупких материалов может быть использована гипотеза прочности Мора, которая для пластичных материалов приводится к третьей гипотезе, а для очень хрупких – к первой гипотезе

.

Расчет балок переменного сечения

Подбор сечений балок равного сопротивления

Все предыдущие расчеты относились к балкам постоянного сечения. На практике мы имеем часто дело с балками, поперечные размеры которых меняются по длине либо постепенно, либо резко.

Ниже рассмотрено несколько примеров подбора сечения и определения деформаций балок переменного профиля.

Так как изгибающие моменты обычно меняются по длине балки то, подбирая ее сечение по наибольшему изгибающему моменту, мы получаем излишний запас материала во всех сечениях балки, кроме того, которому соответствует . Для экономии материала, а также для увеличения в нужных случаях гибкости балок применяют балки равного сопротивления. Под этим названием подразумевают балки, у которых во всех сечениях наибольшее нормальное напряжение одинаково и должно быть равно допускаемому.

Условие, определяющее форму такой балки, имеет вид

и

.

Здесь М(х) и W(x) — изгибающий момент и момент сопротивления в любом сечении балки; W(х) для каждого сечения балки должен меняться пропорционально изгибающему моменту.

Эти условия справедливы и для сечения с наибольшим изгибающим моментом; если обозначить — момент сопротивления балки в сечении с наибольшим изгибающим моментом , то можно написать:

(49)

Покажем ход вычислений на примере. Рассмотрим балку пролетом l, защемленную концом А и нагруженную на другом конце силой Р (рис.7.27). Выберем сечение этой балки в виде прямоугольника; задачу о надлежащем изменении момента сопротивления можно решать, меняя высоту или ширину балки или тот и другой размер вместе.

Рис.7.34

Пусть высота балки будет постоянной , а ширина переменной . Момент сопротивления в сечении на расстоянии х от свободного конца будет , а изгибающий момент ; момент сопротивления опорного сечения , a наибольший изгибающий момент в опорном сечении . В расчете имеют значения лишь абсолютные величины М(х) и .

По формуле (7.40) получаем:

откуда

т. е. ширина меняется по линейному закону в зависимости от х. При ширина равна .

Вид балки в фасаде и плане показан на рис.7.34. Такое очертание балки получается, если учитывать ее прочность только по отношению к нормальным напряжениям; ширина в сечении В обращается в нуль.

Однако необходимо обеспечить прочность и по отношению к касательным напряжениям. Наименьшая ширина балки, требуемая этим условием, определится из уравнения

или, так как

.

Таким образом, исправленное очертание балки предопределяет минимальный размер ширины и утолщение свободного края консоли.