§ 4. Равномерное прямолинейное движение

1. Дополните предложение, вставляя пропущенные слова.

Движение точечного тела называют равномерным прямолинейным, если скорость тела ______________________________.

Закон равномерного прямолинейного движения тела вдоль оси X имеет вид _______________________, где — ______________________________,

а υ_x — ___________________________________________________________.

Если направление скорости точечного тела, движущегося равномерно прямолинейно в трёхмерном пространстве, не совпадает ни с одной из трёх координатных осей, то зависимости его координат от времени имеют вид: x(t) = __________, y(t) = __________, z(t) = _____________, где ___________ __________________________________________________________________.

Путь S, пройденный телом при равномерном прямолинейном движении за время t, равен ______________________________________, где υ — ______________________________________.

2.Отметьте знаком  （галочкой） правильные утверждения.

Примером равномерного прямолинейного движения относительно Земли может быть:

движение камня, брошенного горизонтально; □

движение пассажира, стоящего неподвижно на эскалаторе метро; □

движение электрички от одной станции до другой; □

движение трамвая с постоянной скоростью; □

падение подлетающей к Земле капли дождя в безветренную погоду. □

3. Точечные тела А и В движутся вдоль оси Х так, что их координаты изменяются по законам: а) х_А(t) = 1 + t; б) х_В(t) = 5 – 2t, где x измеряют в метрах, a t — в секундах.

Постройте графики движения тел. Определите по графикам: а) координаты тел в моменты времени 0; 2 и 4 с; б) моменты времени, в которые координаты тел равны 2 и 4 м; в) встретятся ли эти тела (если да, то в какой точке и в какой момент времени)?

Ответ: а) х_А(0) = ______; х_А(2) = ______; х_А(4) = ______;х_В(0) = ______;

х_В(2) = ______; х_В(4) = ______;

б) t_А(2) = ______; t_А(4) = ______; t_В(2) = ______; t_В(4) = ______;

в) х_встр = _____________; t_встр = _____________.

4. На рис. 8 показаны графики движения двух тел вдоль оси X. Определите начальные координаты и проекции скоростей этих тел на эту ось. Запишите законы движения тел.

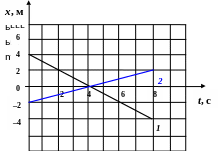
Рис. 8

Ответ: х₁₀ = ______ х₂₀ = _______ v_1х = ________ v_2х = ________

Закон движения тела 1 х₁(t) = __________________

закон движения тела 2 x₂(t) = __________________

5. Точечное тело движется по плоскости XY. На рис. 9 показаны графики зависимости его координат х и y от времени t. Запишите закон движения этого тела в проекциях на координатные оси. Определите модуль скорости этого тела. Постройте траекторию движения тела за первые 5 с.

Рис. 9

Ответ: закон движения тела: х(t) = ___________ y(t) = _____________

Модуль скорости тела v = _______ м/с.

§ 5. Решение задач кинематики равномерного прямолинейного движения. Графический и аналитический способы решения.

Графический способ решения

Задача 1. Из пунктов А и В, находящихся на расстоянии 300 км, одновременно выезжают навстречу друг другу два автомобиля со скоростями, модули которых υ  = 50 км/ч и υ = 100 км/ч. Определите графическим способом время t_в встречи автомобилей и расстояние l от пункта А до места встречи.

Решение.

Шаг 0. Выбор модели.

Будем пренебрегать размерами _____________ и считать, что пункты А и В расположены на одной прямой.

Шаг 1. Выбор системы отсчёта.

В качестве тела отсчёта выберем _________________. За начало отсчёта примем пункт А, в котором находился первый автомобиль в начальный момент времени. Координатную ось X направим __________________________.

Часы (секундомер) включим в начальный момент времени t = 0, соответствующий _____________________.

Шаг 2. Определение начальных координат тел.

В выбранной системе отсчёта начальная координата первого автомобиля равна ____________, а второго — ________________

Шаг 3. Определение проекций скоростей тел на координатную ось.

В выбранной системе отсчёта проекция скорости первого автомобиля на ось X равна __________, а второго автомобиля на ось X равна ______________

Шаг 4. Построение графиков движения тел.

Строим координатную сетку, состоящую из оси времени t (в часах) и оси координаты X (в километрах). Отметим на оси X начальные координаты обоих автомобилей.

Строим графики движения. Так как движение автомобилей равномерное, графики представляют собой _____________________________

Шаг 5. Получение ответа, анализ решения.

Из построения видно, что графики движения автомобилей пересекаются в точке (х_в = ______ км, t_в = _____ ч). Следовательно, в момент времени t_в = ___ (т. е. через _______ после включения секундомера) координаты обоих автомобилей станут равными: ____________________

Таким образом, мы получили ответы на вопросы «Где и когда автомобили встретятся».

Ответ: Машины встретятся на расстоянии l = ________ км от пункта А спустя время t_в = _____ ч после начала движения.

Аналитический способ решения

Задача 2. С Ярославского вокзала вышла электричка, идущая со скоростью, модуль которой υ_э = 60 км/ч. В том же направлении спустя время t₁ = 30 мин вышел скоростной поезд «Спутник», идущий со скоростью, модуль которой υ_с = 90 км/ч. Через какое время t_в после начала движения «Спутника» догонит электричку? На каком расстоянии S от вокзала это произойдёт?

Решение.

Шаг 0. Выбор модели.

Будем считать поезда ________________________________.

Шаг 1. Выбор системы отсчёта.

В качестве тела отсчёта выберем _____________, за начало отсчёта примем ___________________. Координатную ось X направим от ___________________ вдоль путей в направлении ______________________. Часы включим в момент _________________.

Шаг 2. Определение начальных координат тел.

В выбранной системе отсчёта начальная координата «Спутника» _____________________, а электрички — ________________________

Шаг 3. Определение проекций скоростей тел на координатную ось.

В выбранной системе отсчёта направления скоростей обоих поездов совпадает с ____________________ оси X. Поэтому их проекции на ось X ________________ и равны ____________, ____________ соответственно.

Шаг 4. Запись законов движения тел.

Законы движения равномерно движущихся первого и второго поездов с учётом полученных данных имеют вид:

____________________________________________________________

Шаг 5. Запись условия задачи в виде уравнения.

В условии задачи сказано, что в искомый момент времени t_в «Спутник» догнал электричку, т. е. в этот момент времени их координаты стали равными: _______________________________________

Шаг 6. Сведение полученных уравнений в систему и присвоение им названий.

_________________________(2) (закон движения электрички)

_________________________(2) (закон движения «Спутника»)

_________________________(3) (условие встречи)

Шаг 7. Решение системы.

Подставив (1) и (2) для момента времени t = t_в в (3), получим: _________________________________________________________________

Отсюда: t_в = __________, S = _____________

Шаг 8. Анализ полученного результата и расчёт ответа.

Проверка размерности полученных результатов.

[t_в] = _____________ и [S] = _______________.

Таким образом, с точки зрения размерности полученный результат _______________________________________.

Исследуем, как будут изменяться полученные значения S и t_в при изменениях величин, входящих в полученные зависимости.

Если разность модулей скоростей поездов υ – υ стремится к нулю, то _____________. Если увеличивать скорость «Спутника» υ при неизменном υ , то ___________________. Если уменьшать скорость электрички υ при неизменном υ , то ____________________.

Полученные выводы _____________ здравому смыслу и жизненному опыту, т. е. полученные ответы __________ физический смысл.

Проводим численный расчёт, подставив в полученное выражение числовые данные: ________________, ________________

Ответ: Поезда встретятся через t_в = _____ ч на расстоянии S = ______ км от станции.

Задача 3. Пешеход и велосипедист движутся навстречу друг другу со скоростями, модули которых равны 2 м/с и 10 м/с соответственно. Расстояние между ними в начальный момент времени равно 240 м. Найдите графическим и аналитическим способами место и время встречи пешехода и велосипедиста.

Решение.

Задача 4. Колонна длиною L, состоящая из физкультурников, которые следуют друг за другом на равных расстояниях, движется с постоянной по модулю скоростью U. Навстречу им бежит тренер со скоростью, модуль которой равен V (V > U). Каждый спортсмен, с которым поравнялся тренер, мгновенно разворачивается и продолжает движение с прежней по модулю скоростью. Определите длину перестроившейся колонны во главе с тренером.