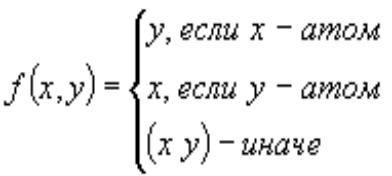Вложенные лямбда-вызовы.

((lambda (x)	((nlambda (x)
((lambda (y)	((lambda (y)
(cons x y)	(cons x y)
)	)
(cdr '(a b c))	(cdr '(a b c))
)	)
)	)
(car '((d e f)))	(car '((d e f)))
)	)

X→(d e f)	X→ (car '((d e f)))
Y→(b c)	Y → (cdr '(a b c))
Результат : ((d e f) b c)	Результат : ((car '((d e f))) cdr '(a b c))

Именованные функции.

Лямбда-выражение есть не имеющий имени механизм, соответствующий используемому в алгоритмических языках определению функции. Для многократного вызова одной и той же функции, но с различными фактическими параметрами функцию необходимо именовать подобно именованию данных посредством функции SET. Дать имя и определить новую функцию можно с помощью функции DEFUN :

(defun <имя> <лямбда-выражение>)

Вызов именованной функции :

(<имя> <список фактических параметров>)

Пример описания и вызова именованной функции :
(defun f1 (list1 list2)	Вызов функции :
((lambda (x y)	(f1 ‘(1 2) ‘(3 4))
((atom x) y)	Результат : 4
((atom y) x)
(cons x y))
(car list1)(cadr list2)))

Современная сокращенная нотация записи именованных функций.

Функция DEFUN соединяет символ имени функции с лямбдавыражением, после чего символ начинает представлять (именовать) определенные этим лямбда-выражением вычисления.

В современной нотации для удобства исключены внешние скобки лямбда-выражения и сам символ LAMBDA :

(defun <имя> (<список формальных параметров>) <тело функции>)

Пример (сокращенная запись для f1) : (defun f2 (list1 list2)

((atom (car list1))(cadr list2)) ((atom (cadr list2)) (car list1)) (cons (car list1) (cadr list2)))

Функции и ветвление.

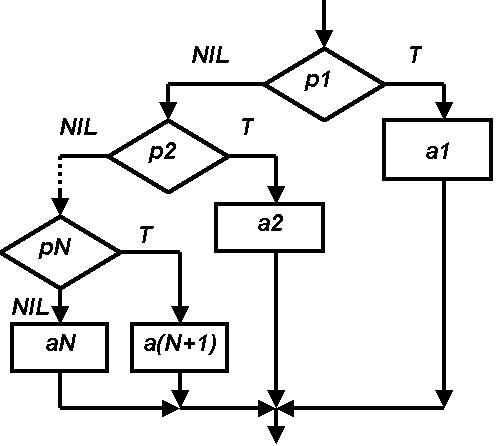
Для разветвления вычислений в Лиспе служит функция COND. Синтаксическая форма COND позволяет управлять вычислениями на основе определяемых предикатами условий.

	Структура условной	Алгоритмический аналог :
	формы :	Алгоритмический аналог :
	формы :
	(cond (p1 a1)
	(p2 a2)
	. . .
	(pN aN)
	a(N+1)
	)
	*Примечание.
	Предикатами pi и
	результирующими
	выражениями ai могут быть
	произвольные формы.

<<< < Предыдущая 12 / 32 3 > Следующая >>>