20) Алгоритм перевода правильных дробей из одной системы счисления в другую.
А) из 10 в любую
- умножить исходную дробь в десятичной системе счисления на основание новой системы счисления, выделить целую часть – она будет первой цифрой новой дроби; отбросить целую часть
- для оставшейся дробной части операцию с выделением целой и дробных частей повторять пока в дробной части не окажется 0 или не будет достигнута желаемая точность конечного числа; появляющиеся при этом целые будут цифрами новой дроби
- записать дробь в виде последовательности цифр и после 0 с разделителем в порядке получения пункта 1 или 2
Б) из любого основания в 10
В этом случае рассчитывается полное значение числа по формуле, причем коэффициенты ai принимают десятичное значение в соответствии с таблицей.
Пример 3.10. Выполнить перевод из двоичной системы счисления в десятичную числа 0,11012. Имеем:
0,11012 = 1*2-1 + 1*2-2 + 0*2-3 +1*2-4 = 0,5 + 0,25 + 0 + 0,0625 = 0,8125.
Расхождение полученного результата с исходным для получения двоичной дроби числом вызвано тем, что процедура перевода в двоичную дробь была прервана.
Таким образом, 0,11012 = 0,8125.
21) Алгоритм перевода целых чисел из одной системы счисления в другую.
А) из 10 основания в другое
Любая позиционная система счисления характеризуется основанием
q - количество знаков или символов, используемых для изображения числа в данной системе
X
10→Xq
Пример:
2510→X3
X = 2213
Б) из любого основания в 10
1023→X10
X = (30*2)+(32*1)+(31+0) = 2+9 = 1110
22) Система счисления. Позиционные и непозиционные системы.
Система счисления это способ представления любого числа с помощью алфавита, символов, называемых цифрами.
Делятся на:
- позиционные
- непозиционные
В непозиционных системах счисления выдаются знаки, которыми записываются ряд основных чисел, а остальные числа получаются как результат сложения или вычитания.
В позиционных системах счисления любое число записывается в виде последовательности цифр, конкретное значение которых зависит от позиции занимаемой каждой из них в числе.
Примеры: десятичная, двоичная, шестнадцатиричная.
23) Основные логические операции.
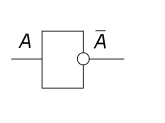
1. Отрицание (инверсия), от латинского inversio -переворачиваю:
соответствует частице НЕ, словосочетанию НЕВЕРНО, ЧТО;
обозначение: не A, A, -A;
таблица истинности:
вход |
выход |
А |
В |
1 |
0 |
0 |
1 |
Инверсия логической переменной истинна, если сама переменная ложна, и, наоборот, инверсия ложна, если переменная истинна.
пример: A = {На улице идет снег}.
A={Не верно, что на улице идет снег}
A={На улице не идет снег};
логическая схема (инвертор):
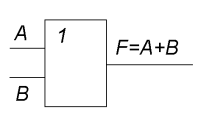
2. Логическое сложение (дизъюнкция), от латинского disjunctio - различаю:
соответствует союзу ИЛИ;
обозначение: +, или, or, V;
таблица истинности:
выход |
вход |
|
А |
В |
С (F) |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
Дизъюнкция ложна тогда и только тогда, когда оба высказывания ложны.
пример: F={На улице светит солнце или дует сильный ветер};
логическая схема (дизъюнктор)
3. Логическое умножение (конъюкция), от латинского conjunctio -связываю:
соответствует союзу И
(в естественном языке: и А, и В
как А, так и В
А вместе с В
А, не смотря на В
А, в то время как В);
обозначение: Ч, •, &, и, ^, and;
таблица истинности:
вход |
выход |
|
А |
В |
С (F) |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
Конъюкция истинна тогда и только тогда, когда оба высказывания истинны.
Например: F={На улице светит солнце и дует сильный ветер};
логическая схема (конъюктор):
4. Импликация (логическое следование), от латинского implicato - тесно связываю:
соответствует речевому обороту ЕСЛИ....ТО
(в естественном языке: если А, то В
В, если А
В необходимо для А
А достаточно для В
А только тогда, когда В
В тогда, когда А
Все А есть В;
обозначение: →;
таблица истинности:
вход |
выход |
||
A |
B |
C |
|
0 |
0 |
0 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
0 |
|
Импликация истинна всегда, за исключением случая, когда А истинно, а В ложно.
пример:
F=A→B
5. Эквиваленция (равнозначность), от латинского aequivalens - равноценные:
соответствует речевым оборотам
ЭКВИВАЛЕНТНО:
необходимо и достаточно для
тогда и только тогда, когда;
обозначение: =, ↔;
таблица истинности:
вход |
выход |
|
A |
B |
A↔B |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
Эквиваленция истинна тогда и только тогда, когда оба высказывания одновременно либо истинны, либо ложны.
пример: Я пойду гулять тогда и только тогда, когда выучу все уроки.