
- •Конспект лекций
- •Раздел I. Множества, функции, отношения. Лекция № 1. Множества и операции над ними.
- •1. Основные понятия теории множеств.
- •2. Операции над множествами и их свойства.
- •3. Векторы и прямые произведения.
- •Лекция № 2. Соответствия и функции.
- •Лекция № 3. Отношения и их свойства.
- •Лекция № 4. Основные виды отношений.
- •Раздел II. Введение в общую алгебру. Лекция № 5. Элементы общей алгебры.
- •1. Свойства бинарных алгебраических операций.
- •2. Алгебраические структуры.
- •Лекция № 6. Различные виды алгебраических структур.
- •Раздел III. Введение в логику. Лекция № 7. Элементы математической логики.
- •Булевы функции.
- •Лекция № 8. Логические функции.
- •Лекция № 9. Булевы алгебры.
- •Лекция № 10. Булевы алгебры и теория множеств.
- •Лекция № 11. Полнота и замкнутость.
- •Лекция № 12. Язык логики предикатов.
- •Лекция № 13. Комбинаторика.
- •Лекция № 15. Маршруты, цепи и циклы.
- •Лекция № 16. Некоторые классы графов и их частей.
Лекция № 12. Язык логики предикатов.
Предикаты.
Определение. Предикатом![]() называется функция
называется функция![]() ,
где
,
где![]() произвольное множество, а
произвольное множество, а![]() определённое ранее двоичное множество
определённое ранее двоичное множество![]() .
.
Иначе говоря,
![]() местным
предикатом, определённым на множестве
местным
предикатом, определённым на множестве![]() называется двузначная функция от
называется двузначная функция от![]() аргументов из произвольного множества
аргументов из произвольного множества![]() .
Множество
.
Множество![]() называетсяпредметной областьюпредиката, переменные
называетсяпредметной областьюпредиката, переменные![]() -предметными переменными. В принципе,
можно определить предикат как функцию
-предметными переменными. В принципе,
можно определить предикат как функцию![]() ,
то есть допустить, что переменные
принимают значения из различных множеств
– в некоторых случаях это оказывается
удобным.
,
то есть допустить, что переменные
принимают значения из различных множеств
– в некоторых случаях это оказывается
удобным.
Для любых
![]() и
и![]() существует взаимно однозначное
соответствие между
существует взаимно однозначное
соответствие между![]() местными
отношениями и
местными
отношениями и![]() местными
предикатами на множестве
местными
предикатами на множестве![]() ,
определяемое следующим образом. Каждому
,
определяемое следующим образом. Каждому![]() местному
отношению
местному
отношению![]() соответствует предикат
соответствует предикат![]() такой, что
такой, что![]() тогда
и только тогда, когда
тогда
и только тогда, когда![]() ;
всякий предикат
;
всякий предикат![]() определяет отношение
определяет отношение![]() такое, что
такое, что![]() тогда и только тогда, когда
тогда и только тогда, когда![]() .
При этом
.
При этом![]() задаётобласть истинностипредиката.
задаётобласть истинностипредиката.
Всякой функции
![]() можно поставить в соответствие
можно поставить в соответствие![]() местный предикат
местный предикат![]() такой, что
такой, что![]() тогда и только тогда, когда
тогда и только тогда, когда![]() .
Поскольку функция должна быть однозначной,
то это соответствие требует, чтобы для
любого
.
Поскольку функция должна быть однозначной,
то это соответствие требует, чтобы для
любого![]() выполнялось
выполнялось![]() .
Поэтому обратное соответствие (от
предиката к функции) возможно только
при выполнении указанного условия.
.
Поэтому обратное соответствие (от
предиката к функции) возможно только
при выполнении указанного условия.
В дальнейшем, в случаях, не вызывающих
разночтения, будем употреблять одинаковые
обозначения для предикатов и соответствующих
им отношений. При этом, помимо функциональных
обозначений вида
![]() ,
для двухместных предикатов будем
пользоваться обозначениями вида
,
для двухместных предикатов будем
пользоваться обозначениями вида![]() ,
которые употреблялись ранее для бинарных
отношений.
,
которые употреблялись ранее для бинарных
отношений.
Пример 1.
а) Предикат
![]() является двухместным предикатом,
предметной областью которого могут
служить любые множества действительных
чисел. Высказывание
является двухместным предикатом,
предметной областью которого могут
служить любые множества действительных
чисел. Высказывание![]() истинно, а высказывание
истинно, а высказывание![]() ложно. Если вместо одной из переменных
подставить число, то получится одноместный
предикат:
ложно. Если вместо одной из переменных
подставить число, то получится одноместный
предикат:![]() и так далее.
и так далее.
б) Великая теорема Ферма (до сих пор не
доказанная) утверждает, что для любого
натурального числа
![]() не существует натуральных чисел
не существует натуральных чисел![]() ,
которые удовлетворяли бы равенству
,
которые удовлетворяли бы равенству![]() .
Этому равенству можно поставить в
соответствие предикат
.
Этому равенству можно поставить в
соответствие предикат![]() ,
истинный тогда и только тогда, когда
оно выполняется.
,
истинный тогда и только тогда, когда
оно выполняется.
в) В описаниях вычислительных процедур
и, в частности, в языках программирования,
часто встречаются указания типа
“повторять цикл до тех пор, пока
переменные
![]() и
и![]() не станут равными или прекратить
вычисление цикла после ста повторений”.
Если обозначить через
не станут равными или прекратить
вычисление цикла после ста повторений”.
Если обозначить через![]() счётчик повторений, то описанное здесь
условие примет вид
счётчик повторений, то описанное здесь
условие примет вид![]() ,
а само указание в целом описывается
выражением: “повторять, если
,
а само указание в целом описывается
выражением: “повторять, если![]() ”.
”.
Кванторы.
Пусть
![]() предикат, определённый на множестве
предикат, определённый на множестве![]() .
Высказывание “для всех
.
Высказывание “для всех![]()
![]() истинно” обозначается
истинно” обозначается![]() или
или![]() .
Здесь множество
.
Здесь множество![]() входит в обозначение, но когда оно ясно
из контекста пишут просто
входит в обозначение, но когда оно ясно
из контекста пишут просто![]() .
Знак
.
Знак![]() называется квантором общности.
называется квантором общности.
Высказывание “существует такое значение
![]() ,
что
,
что![]() истинно” обозначается
истинно” обозначается![]() или
или![]() .
Знак
.
Знак![]() называетсяквантором существования.
Переход от предиката
называетсяквантором существования.
Переход от предиката![]() к выражениям вида
к выражениям вида![]() или
или![]() называетсясвязываниемпеременной
называетсясвязываниемпеременной![]() ,
а такженавешиванием кванторана
переменную
,
а такженавешиванием кванторана
переменную![]() (или на предикат
(или на предикат![]() ).
Переменная, на которую навешен квантор,
называетсясвязанной, несвязанная
переменная называетсясвободной.
).
Переменная, на которую навешен квантор,
называетсясвязанной, несвязанная
переменная называетсясвободной.
Смысл связанных и свободных переменных
в предикатах принципиально различен.
Свободная переменная – это обычная
переменная, которая может принимать
различные значения из множества
![]() ;
выражение
;
выражение![]() - переменное высказывание, зависящее
от значения
- переменное высказывание, зависящее
от значения![]() .
Выражение
.
Выражение![]() не зависит от переменной
не зависит от переменной![]() и имеет вполне определённое значение.
Это, в частности, означает, что
переименование связанной переменной,
то есть переход от выражения
и имеет вполне определённое значение.
Это, в частности, означает, что
переименование связанной переменной,
то есть переход от выражения![]() к выражению
к выражению![]() и наоборот не меняет истинности выражения.
Переменные, являющиеся, по существу,
связанными, встречаются не только в
логике. Например, в выражениях
и наоборот не меняет истинности выражения.
Переменные, являющиеся, по существу,
связанными, встречаются не только в
логике. Например, в выражениях![]() или
или![]() переменная
переменная![]() связана: при фиксированной функции
связана: при фиксированной функции![]() первое выражение равно определенному
числу, а второе становится функцией от
пределов интегрирования.
первое выражение равно определенному
числу, а второе становится функцией от
пределов интегрирования.
Навешивать кванторы можно и на многоместные
предикаты и вообще на любые логические
выражения, которые при этом заключаются
в скобки. Выражение, на которое навешивается
квантор
![]() или
или![]() называется областью действия квантора.
Все вхождения переменной в это выражение
являются связанными. Навешивание
квантора на многоместный предикат
уменьшает в нём количество свободных
переменных и превращает его в предикат
от меньшего числа переменных.
называется областью действия квантора.
Все вхождения переменной в это выражение
являются связанными. Навешивание
квантора на многоместный предикат
уменьшает в нём количество свободных
переменных и превращает его в предикат
от меньшего числа переменных.
Пример 2.
а) Пусть
![]() предикат “
предикат “![]() чётное число”. Тогда высказывание
чётное число”. Тогда высказывание![]() истинно на любом множестве чётных чисел
и ложно, если множество
истинно на любом множестве чётных чисел
и ложно, если множество![]() содержит хотя бы одно нечётное число.
Высказывание
содержит хотя бы одно нечётное число.
Высказывание![]() истинно
на любом множестве, содержащем хотя бы
одно чётное число и ложно на любом
множестве нечётных чисел.
истинно
на любом множестве, содержащем хотя бы
одно чётное число и ложно на любом
множестве нечётных чисел.
б) Рассмотрим двухместный предикат
![]() на множествах
на множествах![]() с отношением нестрогого порядка. Предикат
с отношением нестрогого порядка. Предикат![]() есть одноместный предикат от переменной
есть одноместный предикат от переменной![]() .
Если
.
Если![]() множество неотрицательных чисел, то
этот предикат истинен в единственной
точке
множество неотрицательных чисел, то
этот предикат истинен в единственной
точке![]() .
Предикат
.
Предикат![]() (можно записать
(можно записать![]() ) высказывание истинное на множестве,
состоящем из одного элемента и ложное
на всяком другом множестве. Высказывание
) высказывание истинное на множестве,
состоящем из одного элемента и ложное
на всяком другом множестве. Высказывание![]() утверждает, что в множестве
утверждает, что в множестве![]() имеется максимальный элемент (для любого
имеется максимальный элемент (для любого![]() существует такой
существует такой![]() ,
что
,
что![]() ).
Оно истинно на любом конечном множестве
целых чисел. Высказывание
).
Оно истинно на любом конечном множестве
целых чисел. Высказывание![]() утверждает, что для любого элемента
утверждает, что для любого элемента![]() имеется элемент
имеется элемент![]() ,
не меньший его. Оно истинно на любом
непустом множестве ввиду рефлексивности
отношения
,
не меньший его. Оно истинно на любом
непустом множестве ввиду рефлексивности
отношения![]() .
Последние два высказывания говорят о
том, что перестановка кванторов меняет
смысл высказывания и условие его
истинности.
.
Последние два высказывания говорят о
том, что перестановка кванторов меняет
смысл высказывания и условие его
истинности.
Истинные формулы и эквивалентные соотношения.
При логической (истинностной) интерпретации формул логики возможны три основные ситуации.
Если в области
 для формулы
для формулы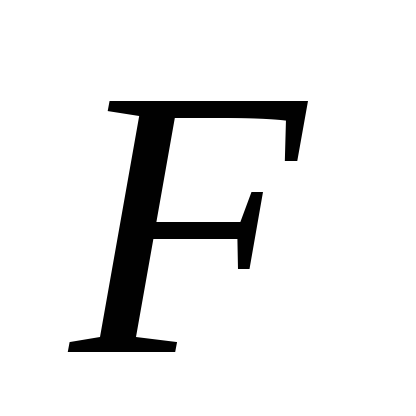 существует такая подстановка констант
вместо всех переменных, что
существует такая подстановка констант
вместо всех переменных, что становится истинным высказыванием, то
эта формула называется выполнимой в
области
становится истинным высказыванием, то
эта формула называется выполнимой в
области 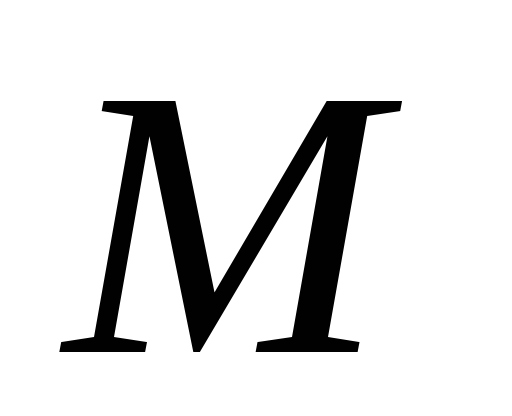 .
Если существует область
.
Если существует область ,
в которой формула
,
в которой формула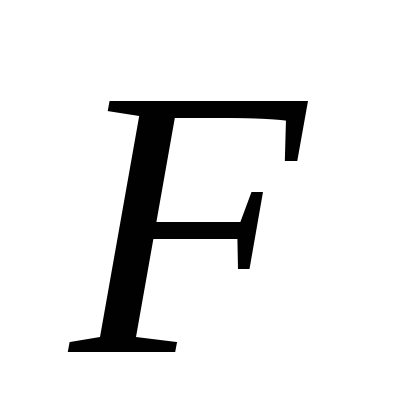 выполнима, то формула называется просто
выполнимой. Пример выполнимой формулы
-
выполнима, то формула называется просто
выполнимой. Пример выполнимой формулы
- .
.Если формула
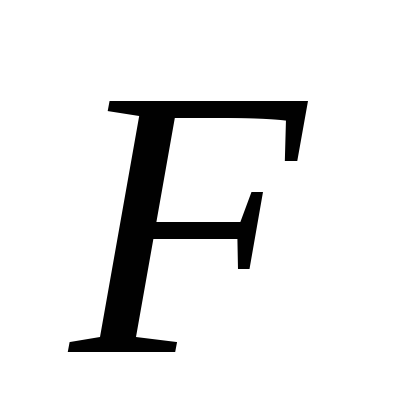 выполнима в области
выполнима в области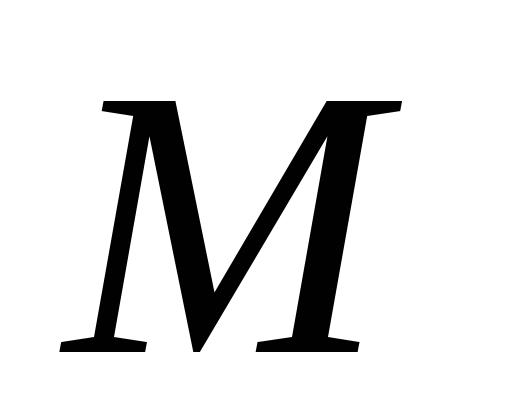 при любых подстановках констант, то
она называетсятождественно истинной
в области
при любых подстановках констант, то
она называетсятождественно истинной
в области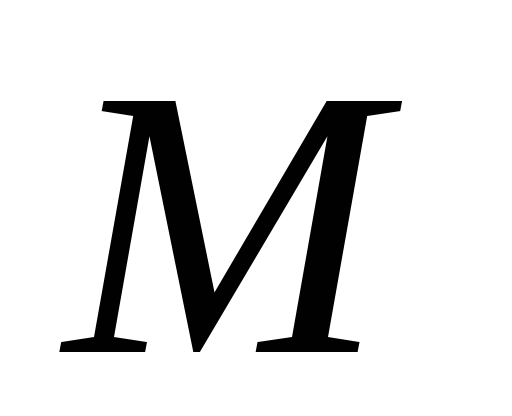 .
Формула, тождественно истинная в любых
множествах называется просто
тождественно истинной, илиобщезначимой,
илитавтологией. Например, формула
.
Формула, тождественно истинная в любых
множествах называется просто
тождественно истинной, илиобщезначимой,
илитавтологией. Например, формула тождественна для всех множеств, состоящих
из одного элемента, а формула
тождественна для всех множеств, состоящих
из одного элемента, а формула является тавтологией.
является тавтологией.Если формула
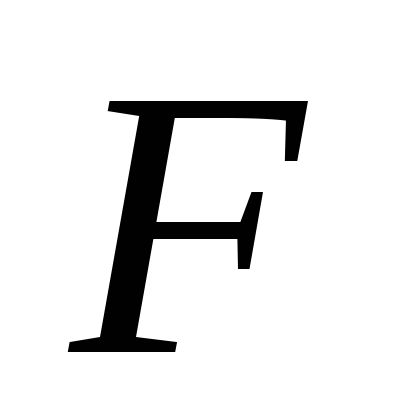 невыполнима в области
невыполнима в области при любых подстановках констант, то
она называетсятождественно ложной
в области
при любых подстановках констант, то
она называетсятождественно ложной
в области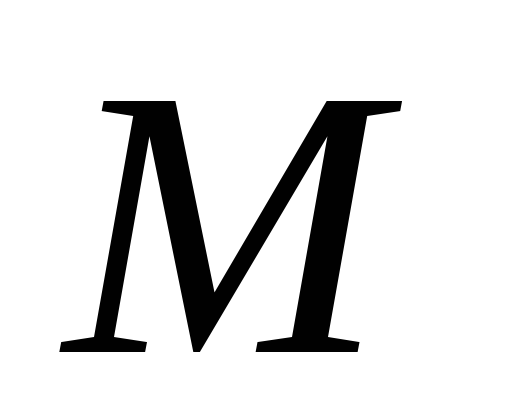 .
Формула, тождественно ложная в любых
множествах называется просто
тождественно ложнойилипротиворечивой.
Формула
.
Формула, тождественно ложная в любых
множествах называется просто
тождественно ложнойилипротиворечивой.
Формула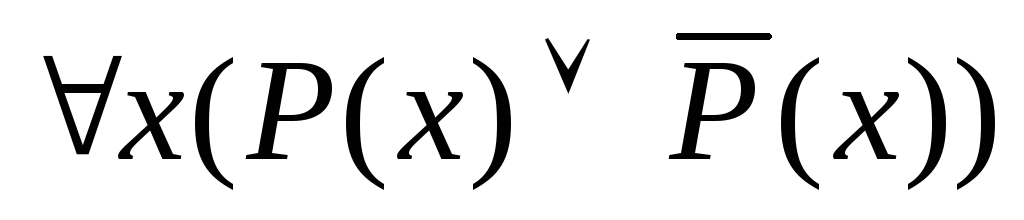 является противоречивой.
является противоречивой.
Определение.Формулы называютсяэквивалентными, если при любых подстановках одинаковых констант они принимают одинаковые значения. В частности, все тождественно истинные (и все тождественно ложные) формулы являются эквивалентными.
Отметим, что если формулы
![]() и
и![]() эквивалентны в соответствии с этим
определением, то формула
эквивалентны в соответствии с этим
определением, то формула![]() является тождественно истинной.
является тождественно истинной.
Замечание. Исследование формул логики предикатов имеет огромное значение потому, что эти формулы входят практически в любую формальную теорию. В связи с этим возникают две проблемы: получение истинных формул и проверка имеющихся формул на истинность. Поскольку предикатные переменные имеют, в общем случае, бесконечное множество значений, то установить истинность формул простым перебором значений на всех наборах переменных, как это иногда делалось для логических функций, просто невозможно. В связи с этим, приходится использовать различные косвенные приёмы.
Пример 3.Рассмотрим соотношение![]() .
Пусть для некоторого предиката
.
Пусть для некоторого предиката![]() и области
и области![]() левая часть истинна. Тогда не существует
такого
левая часть истинна. Тогда не существует
такого![]() ,
для которого
,
для которого![]() истинно.
Следовательно, для любых значений
истинно.
Следовательно, для любых значений![]()
![]() ложно, то есть
ложно, то есть![]() и правая часть истинна. Если же левая
часть ложна, то всегда существует
и правая часть истинна. Если же левая
часть ложна, то всегда существует![]() ,
для которого
,
для которого![]() истинно и, следовательно, правая часть
ложна.
истинно и, следовательно, правая часть
ложна.
Аналогично доказывается истинность
соотношения
![]()
Большое значение имеют следующие свойства, которые могут быть доказаны способом, рассмотренным в примере 3.
Дистрибутивность квантора
 относительно конъюнкции:
относительно конъюнкции:
![]() .
.
Дистрибутивность квантора
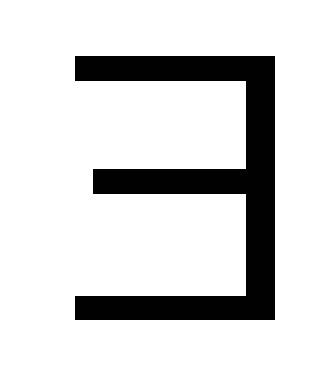 относительно дизъюнкции:
относительно дизъюнкции:
![]() .
.
Если же
кванторы
![]() и
и![]() поменять местами, то получатся соотношения,
верные только в одну сторону:
поменять местами, то получатся соотношения,
верные только в одну сторону:
3)
![]() ,
,
4)
![]() .
.
В таких
случаях говорят, что левая часть является
более сильным утверждением, чем правая,
поскольку она требует для своего
выполнения более жёстких условий. Так,
например, в соотношении 3 в левой части
требуется, чтобы оба предиката были
истинны для одного и того же значения
![]() ,
тогда как в правой части они могут быть
истинны при различных значениях
переменной. Пример случая, когда
соотношения 3 и 4 в обратную сторону
неверны:
,
тогда как в правой части они могут быть
истинны при различных значениях
переменной. Пример случая, когда
соотношения 3 и 4 в обратную сторону
неверны:![]() “
“![]() чётное число”,
чётное число”,![]() “
“![]() нечётное число”.
нечётное число”.
Пусть
![]() некоторое переменное выражение, не
содержащее переменной
некоторое переменное выражение, не
содержащее переменной![]() .
Тогда выполняются соотношения:
.
Тогда выполняются соотношения:
5)
![]() .
.
6)
![]() .
.
7)
![]() .
.
8)
![]() .
.
Эти соотношения
означают, что формулу, не содержащую
переменной
![]() ,
можно выносить за область действия
квантора, связывающего эту переменную.
,
можно выносить за область действия
квантора, связывающего эту переменную.
Доказательства в логике предикатов.
Метод доказательства формул, содержащих
переменные, путём непосредственной
подстановки в них констант называется
методом интерпретаций или методом
моделей. Подстановка констант позволяет
интерпретировать формулу как осмысленное
утверждение об элементах конкретного
множества. Поэтому такой метод, выясняющий
истинность формулы путём обращения к
её возможному смыслу называется
семантическим (смысловым). Метод
интерпретаций удобен для доказательства
выполнимости формул или их неэквивалентности,
поскольку и в том, и в другом случае
достаточно найти одну подходящую
подстановку. Он удобен также для
исследования истинности формул на
конечных областях. Дело в том, что если
область
![]() конечна, то кванторы переходят в конечные
формулы логики высказываний:
конечна, то кванторы переходят в конечные
формулы логики высказываний:
![]() ,
,![]() .
.
Заменяя все кванторы по этим соотношениям, любую формулу логики предикатов можно перевести в формулу, состоящую из предикатов, соединённых логическими операциями. Истинность такой формулы на конечной области проверятся конечным числом подстановок и вычислений. Методы рассуждений, использующие только конечные множества конечных объектов, называются финитными.
Для бесконечных же областей, в общем случае, при доказательстве тождественной истинности формул метод интерпретации связан с большими трудностями. Поэтому для построения множества истинных формул в логике предикатов выбирается иной путь. Это множество порождается из неких исходных формул (аксиом) с помощью формальных процедур - правил вывода. Используются лишь формальные (а не содержательные), внешние свойства последовательности символов, образующих формулы, причём эти свойства полностью описываются правилами вывода. Множества, порождённые таким формальным методом, называются формальными.
Назад, в начало конспекта.
