1.10. Интегрирующий множитель

Определение. Если уравнение не является уравнением в полных дифференциалах и существует функция – такая, что после умножения на неё обеих частей уравнения получающееся дифференциальное уравнение

становится уравнением в полных дифференциалах, т.е. , то функция называется интегрирующим множителем исходного уравнения.

В случае, когда уравнение является уравнением в полных дифференциалах, полагают .

Если найден интегрирующий множитель µ, то интегрирование данного уравнения сводится к умножению обеих его частей на µ и нахождению общего интеграла полученного уравнения в полных дифференциалах.

Если µ есть непрерывно дифференцируемая функция от x и y, то имеем тождество:

.

Из этого тождества следует, что интегрирующий множитель µ удовлетворяет уравнению с частными производными 1-го порядка:

. (10.1)

Если заранее известно, что , где ω – заданная функция от x и y, то уравнение (10.1) сводится к обыкновенному (и притом линейному) уравнению с неизвестной функцией µ от независимой переменной ω:

, (10.2)

где

,

т.е. указанная дробь является функцией только переменной ω.

Решая уравнение (10.2), находим интегрирующий множитель

, .

В частности, уравнение имеет интегрирующий множитель, зависящий только от x ( ) или только от y ( ), если выполнены соответственно следующие условия:

,

или

, .

2. Дифференциальные уравнения 2-го порядка

2.1. Методы понижения порядка уравнения

Дифференциальное уравнение 2-го порядка имеет вид:

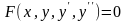
. (1.1)

Общим решением уравнения (1.1) является семейство функций, зависящее от двух произвольных постоянных 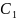и : (или 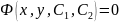– общий интеграл дифференциального уравнения 2-го порядка). Задача Коши для дифференциального уравнения 2-го порядка (1.1) состоит в отыскании частного решения уравнения, удовлетворяющего начальным условиям: при . Необходимо заметить, что графики решений уравнения 2-го порядка могут пересекаться в отличие от графиков решений уравнения 1-го порядка. Однако решение задачи Коши для уравнений 2-го порядка (1.1) при довольно широких предположениях для функций, входящих в уравнение, единственно, т.е. всякие два решения с общим начальным условием совпадают на пересечении интервалов, на которых определены уравнения.

Получить общее решение или решить задачу Коши для дифференциального уравнения 2-го порядка аналитически удаётся далеко не всегда. Однако в некоторых случаях удаётся понизить порядок уравнения с помощью введения различных подстановок. Разберем эти случаи.

1. Уравнения, не содержащие явно независимой переменной . Пусть дифференциальное уравнение 2-го порядка имеет вид:

, (1.2)

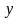
т.е. в уравнении (1.1) явно не присутствует независимая переменная . Это позволяет принять за новый аргумент, а производную 1-го порядка принять за новую функцию . Тогда

Таким образом, уравнение 2-го порядка для функции , не содержащее явно , свелось к уравнению 1-го порядка 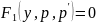для функции . Интегрируя это уравнение, получаем общий интеграл или , а это есть дифференциальное уравнение 1-го порядка для функции . Решая его, получаем общий интеграл исходного дифференциального уравнения (1.2), зависящий от двух произвольных постоянных:

Пример 1. Решить дифференциальное уравнение при заданных начальных условиях:

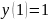
Решение. Так как в исходном уравнении в явном виде отсутствует аргумент , то примем за новую независимую переменную, а – за . Тогда и уравнение для функции приобретает вид:

Последнее уравнение является дифференциальным уравнением с разделяющимися переменными, а значит

.

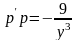
Отсюда следует 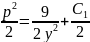, т.е. .

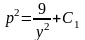
Так как при начальном условии и , то подставляя эти данные в последнее равенство, получаем, что и , откуда . В результате для функции имеем уравнение с разделяющимися переменными, решая которое получаем . Используя начальные условия, получаем, что . Следовательно, частный интеграл уравнения, удовлетворяющий начальным условиям, имеет вид:

2. Уравнения, не содержащие явно искомой функции . Пусть дифференциальное уравнение 2-го порядка имеет вид: , т.е. в уравнение явно не входит искомая функция . В этом случае вводят подстановку . Тогда и уравнение 2-го порядка для функции становится уравнением 1-го порядка для функции . Проинтегрировав его, получаем дифференциальное уравнение 1-го порядка для функции :

Решая последнее уравнение, получаем общий интеграл заданного дифференциального уравнения зависящий от двух произвольных постоянных:

Пример 2. Найти общее решение уравнения: .

Решение. В данное уравнение 2-го порядка явно не входит искомая функция , следовательно, делаем замену: и В результате чего получаем дифференциальное уравнение 1-го порядка для функции :

или

.

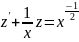Полученное уравнение является линейным уравнением. Решая его, получаем:

или

.

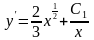
Итак, для функции получили дифференциальное уравнение с разделяющимися переменными:

,

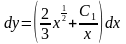
откуда следует общее решение исходного уравнения:

.

3. Порядок степени понижается, если удаётся преобразовать его к такому виду, что обе части уравнения становятся полными производными по x от каких-нибудь функций.

Например, рассмотрим уравнение . Разделяя обе части на получаем

.

Следовательно, порядок уравнения понижен.