Министерство Образования и Науки Российской Федерации
Уфимский Государственный Авиационный Технический Университет
Кафедра высокопроизводительных
вычислительных технологий и систем
Курсовая работа
по предмету: «Численные методы»
на тему: «Решение задачи Дирихле для линейного эллиптического уравнения с переменными коэффициентами методом переменных направлений»
Выполнил: студент группы ПМ 322
И.С. Муратов
Проверил: И.И. Голичев
Уфа 2007г.
Постановка задачи
Методом переменных направлений решить задачу Дирихле для уравнения
,
(1)
(2)
в
области
,
где
–
граница квадрата
.
,
,
,
– точное
решение задачи (1), (2).
Разностная аппроксимация задачи
Задача
Дирихле состоит в следующем. Требуется
найти непрерывную на
функцию
,
удовлетворяющую на открытом квадрате
уравнению (1) и обращается в
на границе квадрата.
Функции
достаточно гладкие, удовлетворяющие
условиям
,
(3)
Задача
Дирихле (1), (2) имеет единственное решение
.
Положим
,
,
,
.
Построим сетки
(
–
множество узлов, лежащих на
)
Заменим исходную дифференциальную задачу (1), (2) разностной задачей.
(4)
на
,
(5)
,
,
.
Введём обозначения:
(6)
(7)
Метод переменных направлений для задачи Дирихле
Напишем для задачи (4), (5) двухслойную разностную схему переменных направлений или дробных шагов
(8)
(9)
.
В
разностной схеме (8), (9) шаг
по времени делится на два полушага.
Разностное уравнение (8) отвечает первому
полушагу, в нём величины
и
считаются уже известными (в частности,
),
а неизвестные имеют верхний индекс
.
Правая часть задана. Перепишем разностное
уравнение (8), предварительно умножив
его на
,
следующим образом:
(10)
и присоединим к разностному уравнению краевые условия
(11)
Разностная
задача (10), (11) распадается на
независимых трёхточечных разностных
краевых задач, отвечающих каждому
фиксированному значению
,
.
Разностная краевая задача (10), (11) решается
методом прогонки при каждом
отдельно. Прогонка осуществляется по
индексу
,
то есть в направлении оси
.
После
того как найдены все неизвестные
на промежуточном слое с номером
,
переносим их в разностном уравнении
(9), соответствующем второму полушагу,
вправо. Это разностное уравнение
переписываем в виде
,
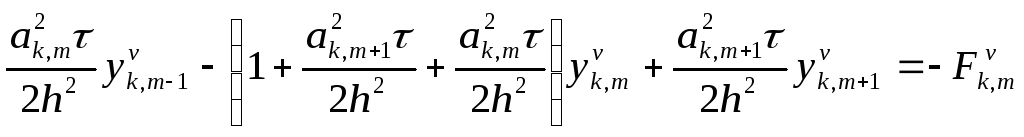(12),
где
известно, и присоединяем к уравнению (12) краевые условия
(13)
Задача
(12), (13) тоже распадается на
независимых трёхточечных разностных
краевых задач, отвечающих каждому
фиксированному
,
.
Каждая такая задача решается методом
прогонки. Прогонка осуществляется
теперь уже по индексу
,
то есть в направлении оси
.
Алгоритм решения задачи Дирихле
-
Начальные условия
– натуральное
число,
шаг по
и по
.
–
начальное приближение. Полагаем
-
Прогонка в направлении оси
Решим
методом прогонки при каждом фиксированном
систему уравнений (10)
,
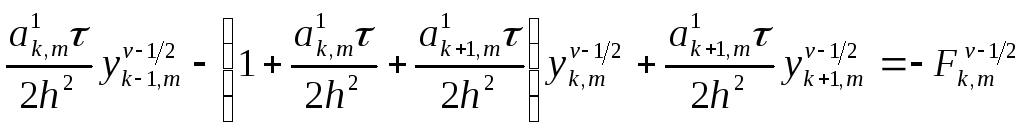Где
известно. Обозначим
,
тогда уравнение (10) мложно записать в виде:
(10*)
Прогонка
осуществляется при каждом фиксированном
.
Прямой ход прогонки
Вычислим
коэффициенты
.
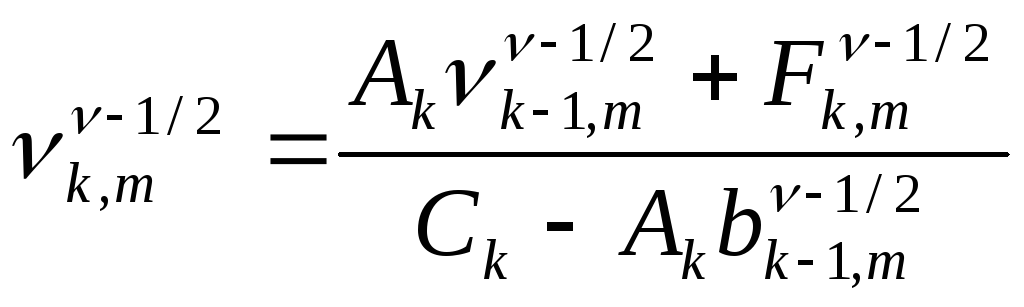
После
того, как будут вычислены коэффициенты
вычислим
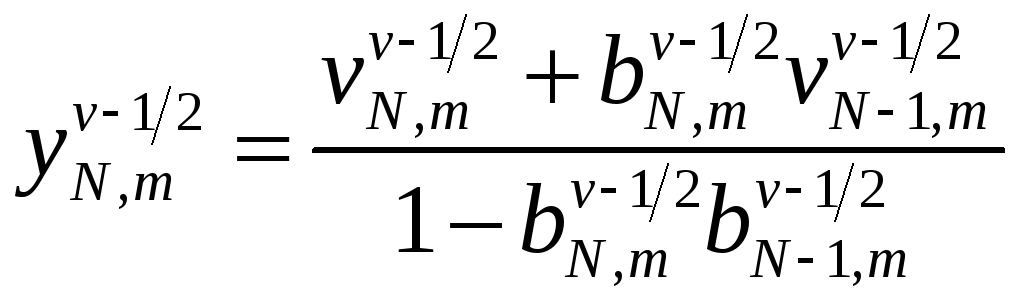
Так
как
,
то получаем
.
Обратный ход прогонки
После
того как будут найдены все
найдём все неизвестные
по формуле
Таким
образом вычисляются
в силу граничных условий.
-
Прогонка в направлении оси
Решим
методом прогонки при каждом фиксированном
систему уравнений (12)
,
где
известно из предыдущих вычислений.
Обозначим
и перепишем систему уравнений (12) в виде:
(12*)
Прогонка
осуществляется при каждом фиксированном
.
Прямой ход прогонки
Вычислим
коэффициенты
.
После
того, как будут вычислены коэффициенты
вычислим
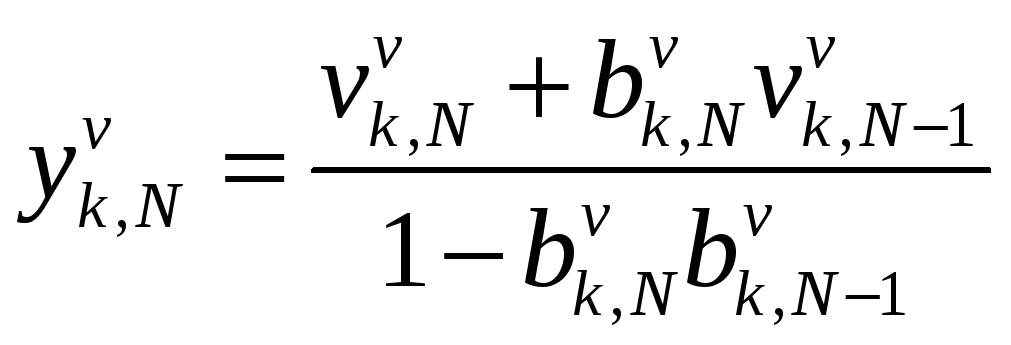
Так
как
,
то получаем
.
Обратный ход прогонки
После
того как будут найдены все
найдём все неизвестные
по формуле
Таким
образом вычисляются
известно из начальных условий.
Результат
В результате выполнения курсовой работы была написана программа на языке C++ реализующая решение задачи Дирихле Методом переменных направлений. Метод сошёлся на третьем временном шаге.
(
,
)-узлы
сетки.
-значение
функции на предпоследнем временном
слое.
-значение
функции на последнем временном слое.
-
точное решение функции.
0 0 0 0 0 0 1 0 0 0 0 2 0 0 0 0 3 0 0 0
1 0 0 0 0 1 1 0.007709 0.007858 0.0081 1 2 0.013724 0.013972 0.0144 1 3 0.01799 0.018304 0.0189
2 0 0 0 0 2 1 0.013896 0.014095 0.0144 2 2 0.024746 0.025076 0.0256 2 3 0.03245 0.032872 0.0336
3 0 0 0 0 3 1 0.018433 0.018618 0.0189 3 2 0.032846 0.033154 0.0336 3 3 0.043094 0.043496 0.0441
4 0 0 0 0 4 1 0.021234 0.021375 0.0216 4 2 0.037873 0.038108 0.0384 4 3 0.049721 0.05004 0.0504
5 0 0 0 0 5 1 0.022248 0.022333 0.0225 5 2 0.039728 0.039875 0.04 5 3 0.052195 0.05241 0.0525
6 0 0 0 0 6 1 0.021442 0.021479 0.0216 6 2 0.038346 0.038414 0.0384 6 3 0.050421 0.050544 0.0504
7 0 0 0 0 7 1 0.018805 0.018808 0.0189 7 2 0.033689 0.033704 0.0336 7 3 0.04434 0.044398 0.0441
8 0 0 0 0 8 1 0.014339 0.014326 0.0144 8 2 0.025741 0.025733 0.0256 8 3 0.033916 0.033942 0.0336
9 0 0 0 0 9 1 0.008061 0.008049 0.0081 9 2 0.014505 0.014497 0.0144 9 3 0.019135 0.01915 0.0189
10 0 0 0 0 10 1 0 0 0 10 2 0 0 0 10 3 0 0 0
0 4 0 0 0 0 5 0 0 0 0 6 0 0 0 0 7 0 0 0
1 4 0.02049 0.02085 0.0216 1 5 0.02126 0.02164 0.0225 1 6 0.02031 0.020697 0.0216 1 7 0.01769 0.01804 0.0189
2 4 0.03699 0.03747 0.0384 2 5 0.03839 0.03892 0.04 2 6 0.03670 0.037257 0.0384 2 7 0.03198 0.03251 0.0336
3 4 0.04914 0.04962 0.0504 3 5 0.05102 0.05157 0.0525 3 6 0.04879 0.049384 0.0504 3 7 0.04252 0.04311 0.0441
4 4 0.05672 0.05712 0.0576 4 5 0.05890 0.05938 0.06 4 6 0.05632 0.056879 0.0576 4 7 0.04907 0.04965 0.0504
5 4 0.05956 0.05986 0.06 5 5 0.06185 0.06225 0.0625 5 6 0.05913 0.059612 0.06 5 7 0.05148 0.05201 0.0525
6 4 0.05756 0.05776 0.0576 6 5 0.05976 0.06006 0.06 6 6 0.05709 0.057501 0.0576 6 7 0.04966 0.05013 0.0504
7 4 0.05063 0.05076 0.0504 7 5 0.05255 0.05278 0.0525 7 6 0.05016 0.050496 0.0504 7 7 0.04357 0.04397 0.0441
8 4 0.03874 0.03882 0.0384 8 5 0.04019 0.04036 0.04 8 6 0.03832 0.038575 0.0384 8 7 0.03322 0.03353 0.0336
9 4 0.02186 0.02191 0.0216 9 5 0.02266 0.02277 0.0225 9 6 0.02158 0.02173 0.0216 9 7 0.01866 0.01885 0.0189
10 4 0 0 0 10 5 0 0 0 10 6 0 0 0 10 7 0 0 0
0 8 0 0 0 0 9 0 0 0 0 10 0 0 0
1 8 0.013415 0.013708 0.0144 1 9 0.007513 0.007694 0.0081 1 10 0 0 0
2 8 0.024272 0.024721 0.0256 2 9 0.013606 0.01389 0.0144 2 10 0 0 0
3 8 0.032276 0.032788 0.0336 3 9 0.018093 0.018426 0.0189 3 10 0 0 0
4 8 0.037231 0.037751 0.0384 4 9 0.020857 0.021204 0.0216 4 10 0 0 0
5 8 0.039021 0.039517 0.04 5 9 0.021831 0.02217 0.0225 5 10 0 0 0
6 8 0.037586 0.038038 0.0384 6 9 0.020987 0.021303 0.0216 6 10 0 0 0
7 8 0.032912 0.033305 0.0336 7 9 0.01833 0.018607 0.0189 7 10 0 0 0
8 8 0.025032 0.025342 0.0256 8 9 0.013895 0.014114 0.0144 8 10 0 0 0
9 8 0.014021 0.014207 0.0144 9 9 0.007751 0.007881 0.0081 9 10 0 0 0
10 8 0 0 0 10 9 0 0 0 10 10 0 0 0