
- •Министерство образования российской федерации.
- •Содержание комплекса.
- •Часть первая. Программа по дисциплине “Численные методы”.
- •Примерный тематический план дисциплины “Численные методы”.
- •Справочная литература.
- •Часть вторая. Конспект лекций по дисциплине “Численные методы”.
- •Лекция №1. Решение нелинейных уравнений. Метод половинного деления.
- •Лекция № 2. Метод итераций для одного уравнения с одним неизвестным.
- •Лекция № 3. Аппроксимация функций. Метод наименьших квадратов.
- •Лекция № 4. Интерполирование функций. Формула Лагранжа.
- •Лекция № 5. Интерполирование функций кубическими сплинами.
- •Лекция № 6. Численное дифференцирование.
- •Лекция № 7. Численное интегрирование.
- •Лекция № 8. Численные методы безусловной оптимизации.
- •Понятие о численном решении задачи Коши.
- •Часть третья. Вопросы к зачёту по дисциплине “Численные методы”.
- •Часть четвёртая. Примеры практических заданий к зачёту по дисциплине “Численные методы”.
- •Часть пятая. Варианты практических заданий зачёту по численным методам.
- •Варианты заданий для практической работы.
- •Задача № 2.
- •Задача № 3.
- •Задача № 4.
- •Задача № 5.
- •Задача № 6.
- •Задача № 7.
- •Задача № 8.
- •Задача № 10
- •Список используемой литературы:
Задача № 7.
Тема:Решение систем нелинейных уравнений с двумя неизвестными методом простых итераций.
F1(x1,x2)
= 0 F2(x1,x2)
= 0![]() методом простых итераций с точностью= 0,01.
методом простых итераций с точностью= 0,01.
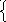
У казание
по выполнению:прежде, чем начать
выполнение задачу необходимо определить
приближённое значение корня данного
уравнения. Это можно сделать графически
или построить таблицу значений функций
на некотором, достаточно обширном,
диапазоне значений аргументов. Описанные
действия можно выполнить с применением
компьютера и электронной таблицыMsExcel. СредствамиMsExcelможно построить в
одной системе координат гладкие графики
функций, соответствующие уравнениям
системы, и с их помощью определить вектор
начального приближения к корню заданной
системы уравнений. Далее, необходимо
преобразовать начальную систему
уравнений к виду:
казание
по выполнению:прежде, чем начать
выполнение задачу необходимо определить
приближённое значение корня данного
уравнения. Это можно сделать графически
или построить таблицу значений функций
на некотором, достаточно обширном,
диапазоне значений аргументов. Описанные
действия можно выполнить с применением
компьютера и электронной таблицыMsExcel. СредствамиMsExcelможно построить в
одной системе координат гладкие графики
функций, соответствующие уравнениям
системы, и с их помощью определить вектор
начального приближения к корню заданной
системы уравнений. Далее, необходимо
преобразовать начальную систему
уравнений к виду:
Д ля
этого необходимо определить частные
производные в точке х0:
ля
этого необходимо определить частные
производные в точке х0:







 F1
;
F1
;
F2
;
F2
.
F1
;
F1
;
F2
;
F2
.
x1 x=x0 x2 x=x0 x1 x=x0 x2 x=x0
Полученные значения частных производных подставляем в системы линейных уравнений (получаем две независимых системы линейных уравнений, каждая из которых содержит две неизвестных):
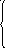
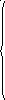 1 +11
1 +11![]() +12
+12![]() = 0
= 0
11![]() +12
+12![]() = 0
= 0
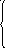 21
21![]() +22
+22![]() = 0
= 0
1 + 21![]() +22
+22![]() = 0
= 0
Из данных систем уравнений находим неизвестные 11,12,21,22. После чего определяем функцииG1(x1,x2) иG2(x1,x2), которые имеют вид:
G1(x1,x2) = х1+11F1(x1,x2) +12F2(x1,x2)
G2(x1,x2) = х2+21F1(x1,x2) +22F2(x1,x2)
После чего, по полученным итерационным формулам выполняются необходимые вычисления для решения данной задачи. Указанная точность вычислений считается достигнутой, если максимальная из разностей (взятой по модулю) координат векторов - корней уравнения, полученных в двух соседних итерациях, по модулю не превышает заданного :
max|xj i+1-xj i)| <,j-номер координаты вектора,i,i+1 – номера итераций.
j=1,2
Результаты выполнения данной задачи определяются правильно выполненной проверкой метода на сходимость и преобразованием уравнений:
 G1(x1,x2)
=x1к виду
G1(x1,x2)
=x1к виду
G2(x1,x2) =x2.
В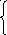 ариант
1.
ариант
1.
 х1>0
х1>0
Вариант 2.

![]() x1<0
x1<0
В ариант
3.
ариант
3.
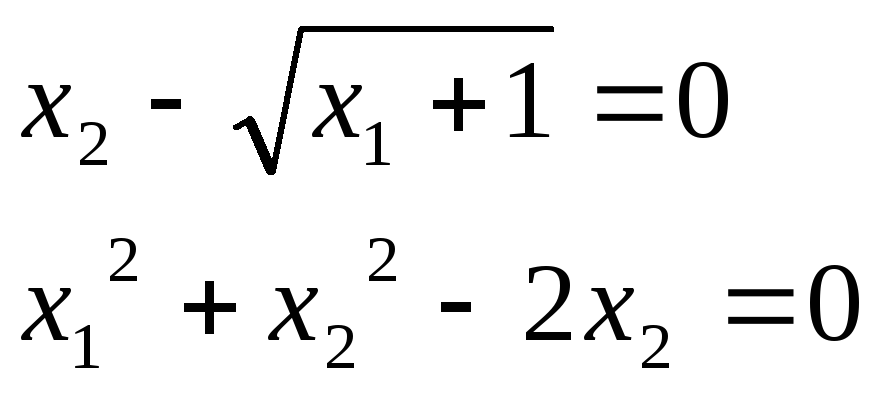 x1 >0
x1 >0
Вариант 4.

 x2<0
x2<0
В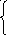 ариант
5.
ариант
5.
![]() x1<0
x1<0
Вариант 6.
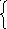
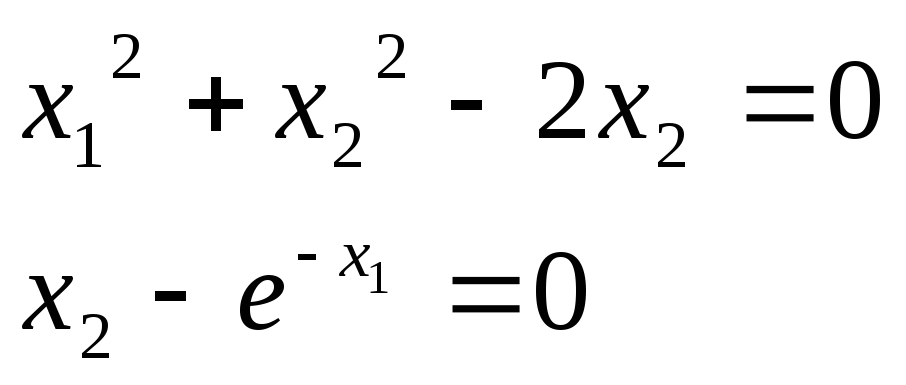 x1>0
x1>0
Вариант 7.

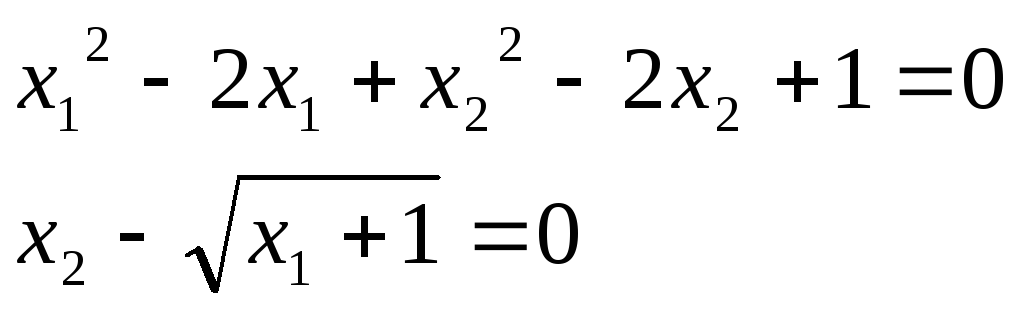 x1>0
x1>0
Вариант 8.

![]() x2>0
x2>0
Вариант 9.
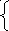
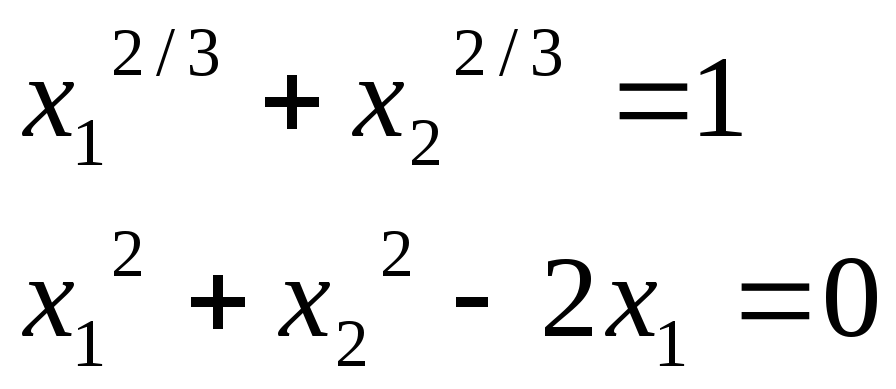 x2>0
x2>0
Вариант 10.

![]() x1>0
x1>0
Задача № 8.
Для функции F(x)
найти значение производной в точках
х01= =1,6 ( х02= 1,8) с шагомh1= 0,1;a1=10 иh2
= 0,05;a2=20 с помощью
формулы:F(x0) .
Найти погрешность решения, используя
формулу:
.
Найти погрешность решения, используя
формулу:![]() .
Погрешность найденного решения не
должна превышать=0.01.
.
Погрешность найденного решения не
должна превышать=0.01.
Для вариантов 1-5 найти значение производной в точке х01= 1,6;
для вариантов 6-10 – в точке х02= =1,8.
Вариант 1. Вариант 2. Вариант 3.
F(x) = 2sin x F(x) = -3 cos x F(x) = tg x
Вариант 4. Вариант 5. Вариант 6.
F(x) = - ctg x F(x) = 4ln x F(x) = sin x
Вариант 7. Вариант 8. Вариант 9.
F(x) = -cos x F(x) =2 tg x F(x) = ln x
Вариант 10.
F(x) = 3ctg x
Задача № 9.
Найти решение задачи Коши для дифференциального уравнения первого порядка на равномерной сетке отрезка [a,b] один раз с шагомh= 0,2, другой – с шагом 0,1 методами Эйлера, Эйлера-Коши и классическим методом Рунге – Кутта. Оценить погрешность численного решения по принципу Рунге. Сравнить численное решение с точным.
Указание по выполнению:для выполнения задания использовать следующие итерационные формулы:
метод Эйлера:р=1 – порядок метода, xi– узлы сетки отрезка [a,b],h– шаг разбиения;xi = xi-1+ h, yi = yi-1 + hf (xi-1, yi-1), i=1, 2, …., m.
метод Эйлера-Коши:р=2 – порядок метода, xi– узлы сетки отрезка [a,b],h– шаг разбиения;xi = xi-1+ h, yi = yi-1 + ∆ yi-1; ∆ yi-1=
 ;
i = 1,2,…,m
;
i = 1,2,…,m
![]()
![]()
3) метод
Рунге-Кутта:р=4 – порядок метода,
xi– узлы сетки
отрезка [a,b],h– шаг разбиения;xi
= xi-1+
h, yi
= yi-1
+ ∆
yi-1;
∆ yi-1=
![]() ;
;
i
= 1,2,…,m;
![]()
![]() ,
,
![]() ,
,
![]() .
.
Для оценки
погрешности найденного решения задачи
Коши используют принцип Рунге (правило
Рунге): εi
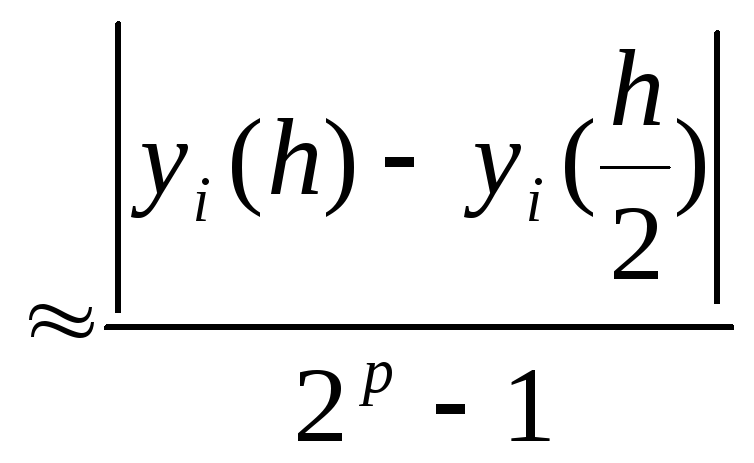
![]()
Вариант 1.
x=1![]()
 y = 0, 1
x
2,
y = 0, 1
x
2,
![]()
Вариант 2.
x=0![]()
 y = 1, 0
x
1,
y = 1, 0
x
1,
![]()
Вариант 3.
x=1![]()
 y = 0, 1
x
2,
y = 0, 1
x
2,
![]()
Вариант 4.
x=0![]()
 , y = 1,
0
x
1,
, y = 1,
0
x
1,
![]()
Вариант 5.
x=1![]()
 y = 1, 1
x
2,
y = 1, 1
x
2,
![]()
Вариант 6.
x=1![]()
 y = 0, 1
x
2,
y = 0, 1
x
2,
![]()
Вариант 7.
x=1![]()
 y = 0, 1
x
2,
y = 0, 1
x
2,
![]()
Вариант 8.
x=0![]()
 y = 0, 0
x
1,
y = 0, 0
x
1,
![]()
Вариант 9.
x=0![]()
 y = 0, 0
x
1,
y = 0, 0
x
1,
![]()
Вариант 10.
![]()
 y = -1, 0
x
1,
y = -1, 0
x
1,
![]()
x=0
