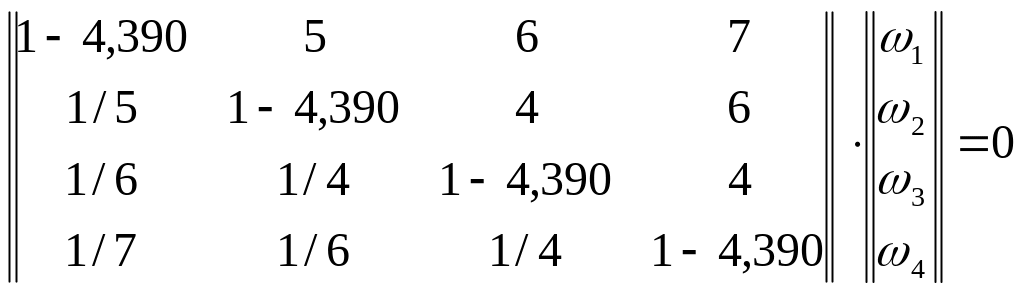Нечеткие отношения

Отношения могут быть заданы перечислением всех пар (u_i,u_j)UU, для которых выполняется отношение R: u₁ R u₂ (отношение R на множестве U).

Четкие отношения:

Нечеткое отношение R определяется как нечеткое подмножество , т. е.

R- отношение «близко к»

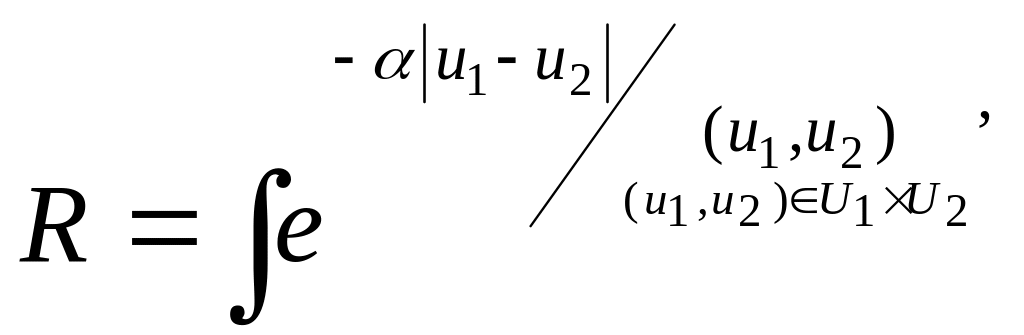
Нечеткое отношение – это нечеткое множество с векторной базовой переменной.

Билет №41

Понятие лингвистической переменной. Числовые и нечисловые лингвистические переменные. Нечеткие числа.

Отличие от численной переменной – её значениями являются не числа, а слова, предложения на естественном или формальном языках. Лингвистическое описание менее точное, чем количественное, тем не менее дает возможность приближенно описывать явления довольно сложные и не поддающиеся описанию в количественных переменных.

ЛП – понятие более высокого порядка, чем нечеткая переменная. Значениями ЛП являются нечеткие переменные (НП).

Определение ЛП:

Х- наименование ЛП;

Т – множество её значений (термов), являющихся наименованиями НП; областью определения каждой из переменных является множество U;

G – синтаксическая процедура (имеющая форму грамматики), порождающая название, исходя из терм-множества (конкретное название х, порожденное G, называется термом);

М – семантическая процедура, которая ставит в соответствие каждой нечеткой переменной её смысл М(х), т.е. нечеткое подмножество М(х) универсального множества U (функция принадлежности).

Пример 1.

Пример 2. Оценка стоимости выпускаемой продукции. Пусть max стоимость 5 тыс. руб.

ЛП=

T – {малая, небольшая, средняя, высокая};

G – процедура перебора элементов множества Т;

М – процедура экспертного опроса, позволяющая дать лингвистическую оценку стоимости.

ЛП – могут быть разделены на числовые и нечисловые. Числовые ЛП – переменная, для которой областью определения Х является подмножество множества действительных чисел R¹. Нечеткие переменные, соответствующие значениям числовой лингвистической переменной называются нечеткими числами. Если множество Х конечно или счётно, то нечеткие числа называются дискретными.

Пример нечисловой ЛП – переменная качества со значениями «удовлетворительное, высокое, невысокое».

К основным вопросам, возникающим при разработке и реализации моделей принятия решений при нечеткой исходной информации, можно отнести следующие:

• построение функций принадлежности нечетких множеств;

• выполнение операций над нечеткими числами;

• сравнение и упорядочение нечетких множеств и чисел;

• разработка моделей принятия решений.

Билет №42.

Арифметические операции над нечеткими числами, сравнение нечетких чисел.

Под нечетким числом будем понимать нечеткое множество с областью определения в виде интервала действительной оси R₁. Пусть А и В – два нечетких числа с носителями S_A =(a_1,a₂) и S_B =(b_1,b₂) соответственно: a₂>a₁ и b₂>b₁.

Согласно принципу обобщения нечеткое число определяется функцией принадлежности:

 = +, -, , /

x=ab

aS_A

bS_B

Первоначально принцип обобщения был введен как некоторый эвристический прием, затем он был получен дедуктивно, а его физический смысл был объяснен в рамках вероятностной интерпретации функции принадлежности.

Носитель S_D нечеткого числа D можно найти по правилам интервальной арифметики

S_D={x:x= ab, aS_A, bS_B}.

Очевидно, что в множестве S_AS_B для любого x S_AS_B , где операция  над носителями нечетких чисел А и В выполняется по правилам интервальной арифметики существует бесконечно много пар (а,b) таких, что x=ab.

Пусть и . Тогда получаем

В случае непрерывных нечетких чисел для вычисления результата выполнения арифметической операции разработано несколько алгоритмов (алгоритм перебора, алгоритм для кусочно-непрерывной функции принадлежности (требуется числовое решение нелинейных уравнений или ряда задач безусловной оптимизации)).

Другой способ вычисления может быть использован в случае треугольных функций принадлежности. Пусть Х - нечеткое число, определим левую , правую границы нечеткого числа и его вершину:

Можно доказать, что нечеткое число также определяется функцией принадлежности треугольного типа, границы и вершина которой находятся следующим образом , , .

Билет №43

Прямые методы построения функций принадлежности нечетких множеств

Во всех случаях функция принадлежности строится методами экспертного опроса. В прямых методах эксперты непосредственно указывают степень принадлежности для каждого элемента. Методы простые, но имеют высокую степень субъективизма. Для уменьшения степени субъективизма используют различные приемы, например:

1. усреднение по числу экспертов;

2. параметрическое представление функции принадлежности.

Рассмотрим более подробно второй прием.

Функции принадлежности треугольного типа:

 x1 x* x11

Левая и правая граница и вершина.

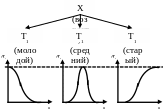
Колоколообразные функции принадлежности (например «Х приближенно равен K»):

 1 0,5 0 а k b

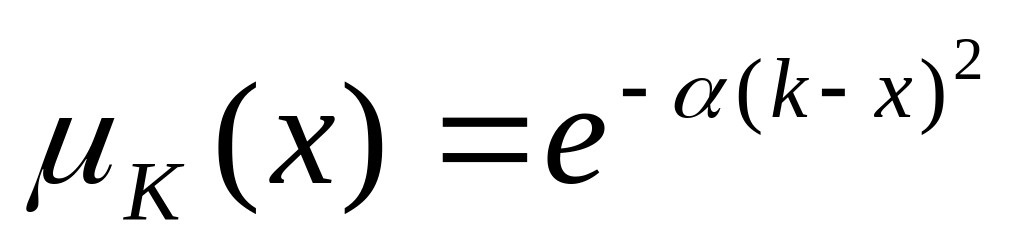
В косвенных методах значения функции принадлежности выбираются таким образом, чтобы удовлетворить заранее сформированным условиям (вычисляются по определенным правилам из информации экспертного опроса).

Метод равноделения (метод психологического шкалирования).

Пусть U – универсальное множество, а u_m и u_M элементы с min и max степенями принадлежностями. Для определенности примем , . Алгоритм метода:

1. найти среднюю по принадлежности точку интервала [u_m,u_М]: u_0,5 ;

2. найти среднюю по принадлежности точку интервала [u_0,5,u_М]: u_0,75;

3. найти среднюю по принадлежности точку интервала [u_m,u_0,5]: u_0,25;

4. найти среднюю по принадлежности точку интервала [u_0,25,u_0,75] для проверки согласованности, если это не u_0,5, то найденные точки изменяются до получения согласованности;

5. шаги 1-4 необходимо повторить для получения большого числа точек;

6. по набору точек 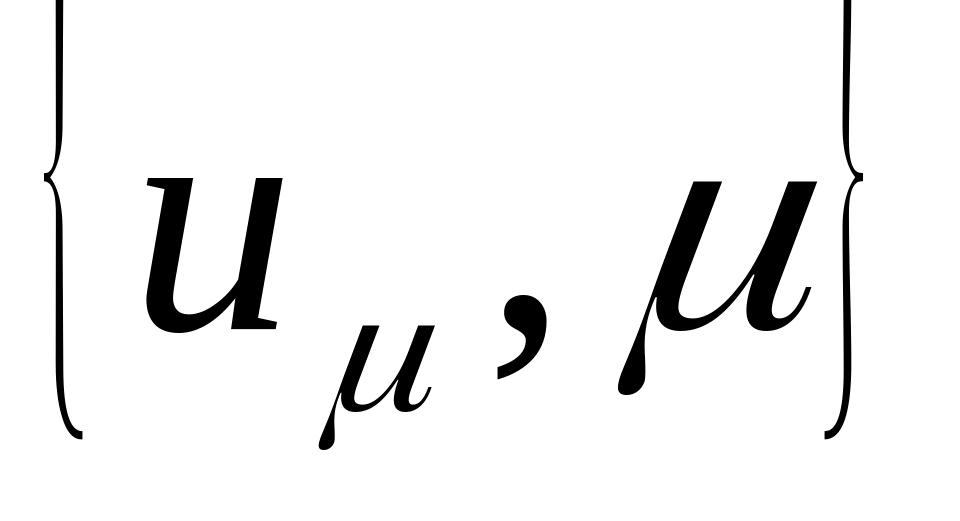определяется искомая функция принадлежности подходящим методом интерполяции.

Билет №44

Косвенные методы построения функций принадлежности нечетких множеств.

Метод попарного сравнения.

Обработка матрицы оценок, отражающих мнение эксперта об относительной принадлежности элементов множеству или степени выраженности у них свойств, формализуемого множеством. Потребуем, чтобы для всех элементов множества S выполнялось равенство .

Степень принадлежности будем определять посредством парных сравнений. Оценка элемента x_i по сравнению с x_j с точки зрения свойства S - . Для обеспечения согласованности примем . Итак, мы имеем матрицу оценок . Найдем собственный вектор матрицы А, решая уравнение , где  собственное значение матрицы А. Вычисленные значения принимаются за . Т.к. всегда выполняется равенство , то найденные значения тем точнее, чем ближе к n. Отклонения от n может служить мерой согласованности суждений экспертов при составлении матрицы оценок.

Нахождение собственного вектора и собственных чисел матрицы.

Иногда приходится рассматривать уравнения типа: , (15.1)

где  - неизвестный числовой вектор, высота которого равна порядку , а  неизвестное число. При любом  уравнение (15.1) обладает тривиальным решением , однако нас будут интересовать только такие , при которых эта система имеет нетривиальные решения, эти значения  называются собственными значениями матрицы А, а решения при таких значениях - её собственными векторами. Преобразуем (15.1), используя очевидное равенство: , тогда получаем (15.2). (15.2) представляет собой систему из n однородных алгебраических уравнений с n неизвестными. Для наличия нетривиального решения необходимо и достаточно, чтобы . Это уравнение называется характеристическим уравнением матрицы , оно служит для разыскания собственных значений  .

Раскрыв определитель, получим алгебраическое уравнение степени n (порядок матрицы А). Матрица прядка «n» имеет «n» собственных значений. Обычно выбирают максимальное по модулю значение.

Найдя какое либо собственное значение , мы можем соответственно собственные вектора найти из (2). Из этого уравнения вытекает, что при зафиксированной  сумма решений будет снова решением, произведение решения на число будет также решением уравнения. Значит, совокупность всех собственных векторов, отвечающих заданному собственному значению, образует линейное пространство (бесконечное число ненулевых решений, система обязательно зависима, т.е. одно уравнение является следствием остальных, одно из уравнений можно отбросить и задавать произвольные значения для одной из переменных). Для нахождения единственного собственного вектора используется замена одного из уравнений условием нормировки.

Пример. Оценка освещенности предмета в зависимости от расстояния до источника: предмет в 9, 15, 21 и 28 единицах длины.

Шкала для определения матрицы суждений

Оценка важности	Качественная оценка	Примечание
1	Одинаковая значимость	По данному критерию альтернативы имеют одинаковый ранг
3	Слабое превосходство	Соображения о предпочтении одной альтернативы перед другой малоубедительны
5	Сильное или существенное превосходство	Имеются надежные доказательства существенного превосходства одной альтернативы
7	Очевидное превосходство	Существуют убедительные свидетельства в пользу одной альтернативы
9	Абсолютное превосходство	В высшей степени убедительное превосходство
2,4,6,8	Промежуточные значения между соседними оценками

Эксперимент дал матрицу . Сначала находим . Для этого составляем уравнение . Эта неоднородная система имеет нетривиальное решение тогда и только тогда, когда определитель матрицы равен 0.

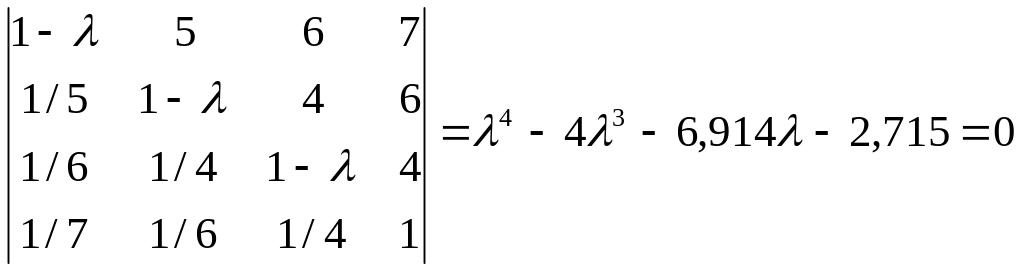
Следовательно

Система имеет только нулевое решение, для нахождения собственного вектора  используется замена одного из уравнений системы условием нормировки 1+2+3+4=1. Решая новую систему, получаем: 1=0,619, 2=0,235, 3=0,101, 4=0,045. (степень согласованности суждений экспертов).

Билет №45

Когнитивное моделирование сложных ситуаций.

С каждым днем возрастает число сложных и очень сложных крупномасштабных систем управления в социально-экономической, экологической, организационной, технической и других сферах. Эти задачи по своей сути являются слабоструктурированными, слабоформализуемыми, содержат многие противоречивые цели и критерии и требуют способов решения задач с нечеткими знаниями, целями и данными. Характерной чертой современных сложных объектов управления яв­ляется также многосвязанность. При решении задач оптимизации управления сложными многосвя­занными системами возникает дополнительная проблема большой раз­мерности. При их реше­нии возникают серьезные неопределенности, связанные с недостаточностью и нечеткостью наших знаний о проблеме, невозможностью учиты­вать реакцию окружающей среды, других лиц на предпринятые действия, а также неопределенности из-за нечетко определенных данных, критери­ев, целей и т.п.

Для выявления базисных социально-политических, экономических, экологических проблем и генерирования рекомендаций по методам управления сложными системами необходимо разработать компьютерные когнитивные модели для качественного моделирования ситуации. Качественные модели сложных и очень сложных систем достаточно эффективно строятся на основе мате­матического аппарата знаковых и взвешенных графов, которые позволя­ют формализовать взаимодействие основных положительных и отрица­тельных обратных связей, существующих между процессами, опреде­ляющими функционирование и развитие сложной социально-политичес­кой, экономической или экологической системы. При построении таких моделей может быть использована неполная, нечеткая и даже противоре­чивая информация.

Цель когнитивной струк­туризации состоит в формировании и уточнении гипотезы о функциони­ровании исследуемого объекта. Чтобы понять и проанализировать пове­дение сложной системы с помощью когнитивного подхода, строится структурная схема причинно-следственных связей. При этом элементы системы А и В , изображаемые на схеме в виде отдельных вершин гра­фа, соединяют ориентированной дугой, если элемент А связан с элемен­том В причинно-следственной связью: А—>В, где А - причина, В -следствие. Рассматриваемые причинно-следственные связи разделяют на положительные и отрицательные. Связь А —> В называется положи­тельной, если увеличение А ведет к увеличению (усилению) В и уменьшение А ведет к уменьшению (ослаблению) В при прочих рав­ных условиях. Отрицательный знак (-) над дугой А —> В означает, что связь отрицательна, т.е. при прочих равных условиях увеличение А при­водит к уменьшению (ослаблению) В. Подобные схемы причинно-следственных связей широко используются для анализа сложных систем в экономике, социологии, в политике, в технике. Такие схемы, интерпре­тирующие мнение, взгляды лица, принимающего решение, называются когнитивной картой. На математическом языке когнитивная карта называется знаковым (взвешенным) ориентированным графом (орграфом). Для определения изменений параметров вершин, с учетом влияния контуров обратной связи пользуются развитием импульсного процесса в знаковых и взвешенных орграфах, который устанавливает, как отклонения одной или нескольких переменных распространяются за не­которое время по структуре графа. Приобретая опыт в анализе знаковых графов, можно избавиться от целого ряда типичных ошибок, свойствен­ных несистемному мышлению. Нередко исследователь ошибочно пред­полагает, что каждое событие имеет только одну причину, не замечая важных обратных связей, как положительных, так и отрицательных.

Когнитивное или графовое моделирование сложных процессов позволяет дать качественные оценки протеканию процессов. Вершины графа соответствуют рассматриваемым процессам, направленные дуги графа отражают влияние процессов друг на друга, а степень такого влия­ния отображается путем приписывания соответствующего веса каждой дуге. Первоначально степень влияния отображается с помощью лингвистических переменных типа «сильно», «умеренно», «слабо» и т.п. В зави­симости от совокупности значений той или иной лингвистической пере­менной выбирают числовую шкалу соответствующей метрики; с помо­щью таких шкал качественным значениям переменных присваивают оп­ределенные числовые значения по соответствующим шкалам, в результа­те получаем взвешенный ориентированный граф.

Если графовая модель среды достаточно правдоподобна, то постав­ленные цели можно интерпретировать в терминах моделей как подмно­жество «благоприятных» ситуаций. Под допустимым решением будем понимать решение, переводящее систему в какую-либо благоприятную ситуацию и удерживающую ее в этой ситуации. Процесс такого перевода назовем управлением ситуациями, а переводимые ситуации - управляе­мыми ситуациями.