Построение моделей идентификации поисковыми методами

При нелинейной параметризации дело обстоит сложнее. Приходится решать систему нелинейных уравнений. Для этого можно использовать методы последовательного приближения.

Предположим, что y (функция отклика) – доля химического вещества А, оставшаяся к моменту времени x₁ в результате реакции типа А→В. Зависимая переменная y удовлетворяет дифференционному уравнению (известно из литературы): , где K – константа скорости. Решение этого уравнения при следующих начальных условиях: у=1 при х=0 имеет вид: у= exp (-К х₁); K зависит от абсолютной температуры х₂ следующим образом:

К= b₁ ехр (-b₂ / х₂) , b₁ – предэкпоненциальный множитель, b₂ – энергия активации. Модель процесса

(6.11)

нелинейна по параметрам b₁, b₂ .

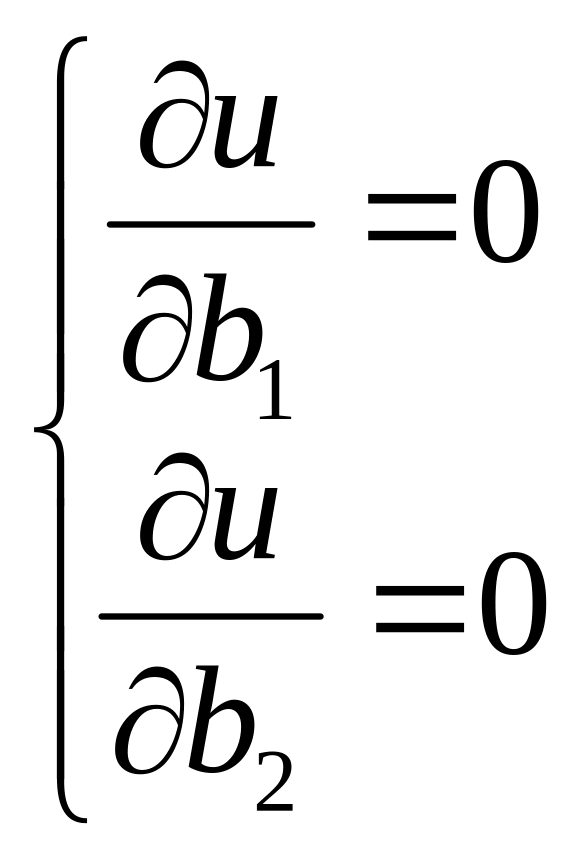
Если ввести то

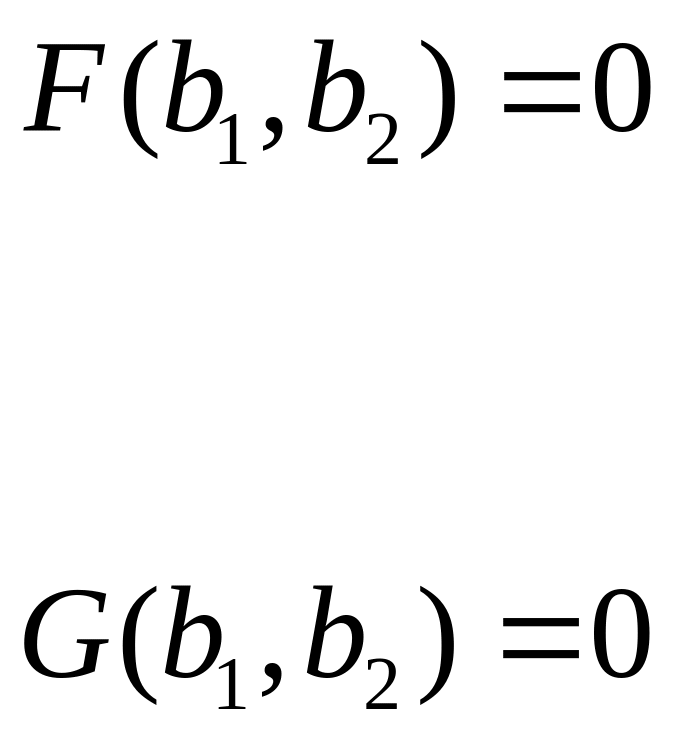
Начальные (нулевые) значения параметров b₁⁰,b₂⁰ могут быть получены методом линеаризации:

ln у = - b₁х₁ ехр ( -b₂ / х₂); ln у (- ln у) = ln b₁ - b₂ / х₂ + ln х₁ или

, где , , , .

Поисковые методы идентификации. В этих методах принятый критерий невязки (показатель качества идентификации) формируется из выходных характеристик объекта и его идентифицируемой модели и минимизируется с помощью численных методов. Итерационный процесс изменения вектора идентифицируемых параметров определяется используемым алгоритмом (методом) поиска и текущей ситуацией.

Билет №10

Математическое моделирование сложных неоднородных систем. Математические модели элементов систем.

При построении математических моделей сложных технических систем эффективным оказывается их последовательное расчленение на подсистемы (декомпозиция системы) с сохранением связей между выявленными подсистемами. Процедура декомпозиции осуществляется до получения таких подсистем, которые в условиях рассматриваемой задачи будут признаны достаточно простыми и удобными для непосредственного математического описания. Эти подсистемы, не подлежащие дальнейшей декомпозиции, называются элементами сложной системы.

Таким образом, в общем случае сложная система является многоуровневой иерархической конструкцией из взаимодействующих элементов, объединяемых в подсистемы различных уровней. Представление моделируемого объекта в виде многоуровневой системы называется его структуризацией. Математическая модель сложной системы образуется композицией (в рамках выделенной структуры) математических моделей элементов и взаимодействий между ними.

Построение простой и изящной математической модели, достаточно точно описывающей процесс функционирования сложной системы, требует немалого искусства. Необходимо знать типичные математические схемы.

Математические модели широкого класса детерминированных объектов (при описании которых влияние случайных факторов не учитывается), функционирующих в непрерывном времени, описываются чаще всего дифференциальными уравнениями в обыкновенных или частных производных.

Детерминированные объекты, функционирующие в дискретном времени, описываются математическими моделями, сводящимися к различным типам конечных автоматов.

Абстрактно конечный автомат представляет собой математическую схему, характеризующуюся 6 элементами:

1. конечным множеством X входных сигналов (входной алфавит);

2. конечным множеством Z внутренних состояний (алфавитом состояний);

3. конечным множеством Y (выходным алфавитом);

4. начальным состоянием z₀;

5. функцией переходов φ (x,z);

6. функцией выходов (z,y).

По числу состояний различают конечные автоматы с памятью и без памяти. Автоматы с памятью имеют более одного состояния, а автоматы без памяти (комбинационные или логические) обладают лишь одним состоянием.

По характеру отсчета дискретного времени конечные автоматы делятся на синхронные и асинхронные.

Билет №11

Математическая модель взаимодействия элементов сложной системы. Механизм обмена сигналами. Схема сопряжения элементов.

Взаимодействие элементов в процессе функционирования сложной системы рассматривается как результат совокупности воздействий каждого элемента на другие элементы. Воздействие представленное набором своих характеристик, часто называют сигналом, т.о. взаимодействие элементов сложной системы может быть рассмотрено в рамках механизма обмена сигналами. Сигналы передаются по каналам связи между элементами. Начало данного канала – выходной полюс, конец канала – входной полюс элемента. Идеальным каналом называется канал, в котором передача сигнала осуществляется мгновенно и без искажений. Полностью и правильно формализованная система имеет только идеальные каналы связей. Физические каналы связи не являются идеальными. Такие каналы связи необходимо рассматривать как самостоятельные элементы системы (электрические соединительные провода – отдельные резисторы), функционирование которых сводится к соответствующим задержкам и искажениям сигнала. При построении математической модели сложной системы необходимо учитывать взаимодействие её с внешней средой. Внешняя среда рассматривается как некоторая совокупность объектов, воздействующих на элементы сложной системы, а также испытывающих воздействия, поступающие от элементов сложной системы. Механизм обмена сигналами и формализованная схема взаимодействия элементов сложной системы между собой и с объектами внешней среды включает наборы следующих составляющих:

1. процесс формирования выходного сигнала соответствующим элементом системы;

2. определение адреса передачи для каждого выходного сигнала;

3. прохождение сигналов по каналам связи и компоновка входных сигналов для элементов системы, принимающих сигналы.

4. реагирование элементов на поступающие входные сигналы.

Первая и четвертая составляющие описываются в рамках математических моделей элементов. Третья составляющая связана с заменой реальных физических каналов идеальными. Вторая составляющая механизма обмена сигналами в сложной системе обеспечивает адресацию характеристик выходных сигналов и их компоновку во входные сигналы элементов, т.е. схему сопряжения элементов (иногда говорят структуру связности).

Схема сопряжения элементов системы. Пусть сложная система S содержит элементы C₁, C₂..C_N. Предположение 1. Элементарные сигналы передаются в системе по элементарным каналам: каждый l-ый элементарный канал, подключенный к выходу элемента С_j, способен передавать только элементарные сигналы y_l^(j), имеющие фиксированный индекс l. Внешнюю среду можно представить в виде фиктивного элемента C₀ системы S, вход которого содержит m₀ входных контактов X_i⁽⁰⁾, а выход r₀ выходных контактов Y_l⁽⁰⁾. Каждый С_j (в том числе и С₀) как элемент системы S в рамках принятых предположений о механизме обмена сигналами, достаточно характеризовать множеством входных контактов которые мы будем обозначать и множеством выходных контактов обозначаемым , где для простоты приняты обозначения m=m_j; r=r_j; j=0,1,..N.

Другими словами, математической моделью элемента С_j, используемой для формального описания сопряжения его с прочими элементами системой и внешней средой, является пара множеств: и . Для исключения неоднозначности введем предположение 2: ко входному контакту любого элемента системы подключается не более чем один элементарный канал; к выходному контакту может быть подключено любое конечное число элементарных каналов, при условии, что ко входу одного и того же элемента системы направляется не более чем один из упомянутых элементарных каналов.

Рассмотрим множество всех входных контактов всех элементов системы и внешней среды , а также всех выходных контактов . В силу второго предположения каждому входному контакту соответствует не более чем один выходной контакт , с которым он связан элементарным каналом. Поэтому можно ввести однозначный оператор =R( ) (7.4) с областью определения во множестве и областью значений во множестве , сопоставляющий входному контакту выходной контакт , связанный с ним элементарным каналом. Если в рассматриваемой системе к данному контакту не подключен никакой элементарный канал, то оператор (7.4) не определен на этом . Совокупность множеств и и оператора R будем называть схемой сопряжения элементов в системе S, а оператор R- оператором сопряжения. Оператор сопряжения можно задать в виде таблицы, в которой на пересечении строк с номерами элементов системы j и столбцов с номерами контактов i располагаются пары чисел (k,l), указывающие номер элемента k и номер контакта l, с которым соединен контакт .

i j	1	2	3	4	5
0	1,1	3,1	4,1	5,1	6,2
1	0,1
2	1,3	0,2	0,3
3	1,2	2,1
4	3,2	2,1	2,2
5	2,2
6	5,2	0,4

Другой способ задания оператора R получим, если столбцы и строки таблицы нумеровать двойными номерами (j,i) и (k,l) соответственно, а на пересечениях помещать 1 для контактов и , соединенных элементарным каналом и 0 в противном случае. Хотя таблицы такого рода громоздки, они не редко находят применение, т.к. представляют собой матрицы смежности ориентированных графов, вершинами которых являются контакты, а ребрами – элементарными каналы. Заметим, что соответствие между и , описываемое оператором R, не является взаимно однозначным (один и тот же выход может направляться на входы разных элементов). Рассмотрим сужение оператора R на множество , т.е. оператор R_j, определенный для данного элемента системы С_j (строка в таблице с номером j). Соответствие, описываемое оператором R_j для j=0,1,..N является взаимно однозначным, в силу второй части второго предположения. Поэтому существует однозначный обратный оператор R_j^-1, сопоставляющий каждому контакту из множества R( ) соответствующий контакт . Схема сопряжения, задаваемая множествами , и оператором R, содержит исчерпывающие сведения о соединениях элементов системы элементарными каналами.

Математическим описанием элементов сложной системы на единой концептуальной основе и построением соответствующей схемы сопряжения элементов исчерпывается проблема построения математической модели функционирования сложной системы.

Билет №12

Марковский случайный процесс. Классификация марковских процессов.

Для вычисления числовых параметров, характеризующих стохастические объекты, нужно построить некоторую вероятностную модель явления, учитывающую сопровождающие его случайные факторы. Для математического описания многих явлений, развивающихся в форме случайного процесса, может быть с успехом применен математический аппарат, разработанный в теории вероятностей для так называемых марковских случайных процессов. Поясним это понятие. Пусть имеется некоторая физическая система S, состояние которой меняется с течением времени (под системой S может пониматься что угодно: техническое устройство, ремонтная мастерская, вычислительная машина и т.д.). Если состояние S меняется по времени случайным образом, говорят, что в системе S протекает случайный процесс. Примеры: процесс функционирования ЭВМ (поступление заказов на ЭВМ, вид этих заказов, случайные выходы из строя), процесс наведения на цель управляемой ракеты (случайные возмущения (помехи) в системе управления ракетой), процесс обслуживания клиентов в парикмахерской или ремонтной мастерской (случайный характер потока заявок (требований), поступивших со стороны клиентов).

Случайный процесс называется марковским процессом (или «процессом без последствия»), если для каждого момента времени t₀ вероятность любого состояния системы в будущем (при t t₀) зависит только от её состояния в настоящем (при t= t₀) и не зависит от того, когда и каким образом система пришла в это состояние (т.е. как развивался процесс в прошлом). Пусть S техническое устройство, которое характеризуется некоторой степенью изношенности S. Нас интересует, как оно будет работать дальше. В первом приближении характеристики работы системы в будущем (частота отказов, потребность в ремонте) зависят от состояния устройства в настоящий момент и не зависят от того, когда и как устройство достигло своего настоящего состояния.

Теория марковских случайных процессов – обширный раздел теории вероятности с широким спектром приложений (физические явления типа диффузии или перемешивания шихта во время плавки в доменной печи, процессы образования очередей).