
- •Вопрос 1.Радиус-вектор.Вектор перемещения.
- •Вопрос 2.Скорость перемещения. Средняя и мгновенная скорости.
- •Вопрос 4.Ускорение.Модуль ускорения.
- •Вопрос 5.Неравномерное движение точки по криволинейной траектории.
- •Тема 5. Законы ньютона.
- •Вопрос 1. Инерциальные системы отсчета. Первый закон Ньютона.
- •Вопрос 2. Второй закон Ньютона.
- •Вопрос 3. Третий закон Ньютона.
- •Вопрос 4. Полный импульс системы.
- •Вопрос 5. Центр масс(центр инерции). Уравнение движения центра масс.
- •Тема 6. Закон сохранения импульса.
- •Вопрос 1. Замкнутая и незамкнутая системы в механике. Закон сохранения импульса.
- •Тема 7. Работа. Мощность. Энергия.
- •Вопрос 1. Определение элементарной работы, различные выражения.
- •Вопрос 2. Мощность, ее выражение через силу и скорость тела.
- •Вопрос 3. Кинетическая энергия и ее выражение через импульс тела.
- •Вопрос 4. Консервативные силы, их работа. Потенциальная энергия.
- •Вопрос 3. Получить выражение для момента инерции.
- •Вопрос 4. Основной закон динамики для вращения тела вокруг неподвижной оси.
- •Вопрос 5. Плоские движения твердого тела.
- •Вопрос 7. Кинетическая энергия при вращательном движении.
- •Тема 9. Закон сохранения момента импульса.
- •Вопрос 1. Получить закон сохранения момента импульса.
- •Тема 10. Силовые поля
- •Вопрос 1. Понятие поля. Поля консервативных сил.
- •Вопрос 2.Потенциальные кривые
- •Вопрос 4.Получить выражение потенциальной энергии
- •Тема 11.Принцип относительности в механике
- •Вопрос 1.Принцип относительности Галилея.
- •Вопрос 2. Постулаты специальной теории относительности(сто).
- •Вопрос 3. Сокращение длины.
- •Вопрос 4. Замедление времени.
- •Вопрос 5. Интервал между событиями.
- •Вопрос 6. Релятивистский закон сложения скоростей.
- •Вопрос 7. Кинетич. Энергия релятивистской частицы. Энергия покоя. Полная энергия.
- •Вопрос 8.Релятивистский Импульс.
- •Вопрос 9.Взаимосвязь массы и энергии в теории относительности.
- •Тема 12. Молекулярная физика.
- •Вопрос 1.Молекулярные системы.
- •Вопрос 2.Идеальный газ
- •Вопрос 3.Основные уравнения мкт
- •Вопрос 4.Средняя кинетическая энергия
- •Вопрос 5.Степени свободы молекул.
- •Тема 13.Классическая статика.
- •Вопрос 1.Распределение молекул по скоростям(Закон Максвелла).
- •Вопрос 2. Средняя арифметическая и средняя квадратичная скорости
- •Вопрос 3.Барометрическая формула. Закон Больцмана.
- •Тема 14. Явления переноса в газах
- •Вопрос 1.Столкновение молекул.
- •Вопрос 2.Диффузия.
- •Вопрос 3.Вязкость (внутреннее трение)
- •Вопрос 4.Теплопроводность
- •Тема 15. Основные понятия термодинамики
- •Вопрос 1. Основные понятия. Обратимые и необратимые процессы.
- •Вопрос 2. Первое начало термодинамики.
- •Вопрос 3.Изохорический процесс. Его можно осуществить, нагревая газ при закрепленном поршне. Подставим выражения для dQ и dU.
- •Вопрос 7.Работа.
- •Вопрос 8.Теплоемкость газов.
- •Тема 16.
- •Вопрос 1. Энтропия
- •Вопрос 2,3,4. Изобарический, изохорический, изотермический
- •Вопрос 6.Теперь мы можем сформулировать II начало термодинамики.
- •Вопрос 7. Круговые процессы (циклы)
- •Тема 18.Вопрос 1.Агрегатные состояния вещества
- •Тема 17.Вопрос 1. Реальные газы
- •Вопрос 2.Состояние реальных газов. Уравнение Ван-дер-Ваальса
- •Вопрос 3. Изотермы реального газа
- •Вопрос 4.Внутреняя энергия реального газа.Эффект джоуля-томсона.
- •Тема 18. Вопрос 2. Жидкости
- •Вопрос 3.
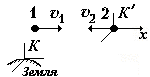
Вопрос 6. Релятивистский закон сложения скоростей.
Найдем скорость 1-го фотона в системе отсчета К, связанной со 2-ым фотоном, используя классическую формулу для сложения скоростей:
|
классическая формула сложения скоростей в векторной форме |
|
|
для 1-го фотона в проекциях, v1 –скорость 1-го в К, v1 – скорость 1-го в К, v2 – скорость 2-го, т.е. скорость К в К. |
|
|
Найдем v1 , учитывая, что v1 = v2 = с |
Таким образом, скорость одного фотона в системе отсчета, связанной со 2-ым, оказалась равной 2с, но согласно СТО ни одна частица не может двигаться со скоростью, большей скорости света.
|
релятивистская формула сложения скоростей u – скорость тела в неподвижной системе отсчета К, u - скорость тела в движущейся системе отсчета К , v – скорость системы К относительно системы К |
|
Вычислим теперь скорость фотона из предыдущего примера по релятивистской формуле.
|
Вопрос 7. Кинетич. Энергия релятивистской частицы. Энергия покоя. Полная энергия.
Найдем выражение для кинетической энергии в СТО, считая, что приращение кинетической энергии происходит за счет работы некоторой силы. Тело в начальный момент неподвижно и является свободным, т.е. не взаимодействует с другими телами и не обладает, таким образом, потенциальной энергией.
|
чтобы проинтегрировать
и получить
|
||
|
вместо переменной
р
появились переменные
|
||
|
здесь уже нет
векторных произведений т.к.
|
||
|
возведем в квадрат, выразим
|
||
|
теперь можно проинтегрировать , т.к. осталась одна переменная m |
||
|
интегрируя, получим выражение для кинетической энергии в СТО |
||
|
Релятивистская кинетическая энергия |
|
энергия покоя |
|
полная релятивистская энергия, т.е. энергия движущегося тела |
|
При v<<c релятивистское выражение переходит в класи. |
Вопрос 8.Релятивистский Импульс.
При использовании преобразований Лоренца основной закон динамики m(dp/dt) = F оказывается инвариантным при условии, что импульс частицы записывается в виде:
|
Релятивистский импульс частицы |
|
основной закон релятивистской динамики |
|
Величина m называется релятивистской массой, она зависит от скорости тела и не является инвариантом, т.е. имеет различное значение в разных ИСО. |
m0 – масса тела, называемая также массой покоя, является инвариантом и имеет одно и то же значение в любых ИСО.
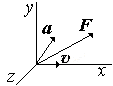 В классической
механике ускорение частицы и сила,
вызвавшая это ускорение, всегда направлены
одинаково. При скорости движения частицы
сопоставимой со скоростью света, т.е. в
релятивистском случае, направление
ускорения и силы совпадают только в
двух случаях: 1) когда сила параллельна
скорости в каждый момент времени и 2)
когда сила перпендикулярна скорости.
В общем случае направления ускорения
и силы не совпадают (см. рис)
В классической
механике ускорение частицы и сила,
вызвавшая это ускорение, всегда направлены
одинаково. При скорости движения частицы
сопоставимой со скоростью света, т.е. в
релятивистском случае, направление
ускорения и силы совпадают только в
двух случаях: 1) когда сила параллельна
скорости в каждый момент времени и 2)
когда сила перпендикулярна скорости.
В общем случае направления ускорения
и силы не совпадают (см. рис)
Из СТО следует возможность существования частиц с нулевой массой, но они не могут быть неподвижными, а должны непрерывно двигаться, причем только со скоростью света с – это фотоны и, возможно, нейтрино.
|
связь энергии и импульса для частиц с нулевой массой (фотонов) m0 = 0 |
|
Некоторые формулы из СТО, которые можно вывести из приведенных выше выражений |
||
|
связь кинетической энергии частицы с ее импульсом |
|
|
связь полной энергии частицы с ее импульсом |
|
|
связь полной энергии и энергии покоя с импульсом |
|

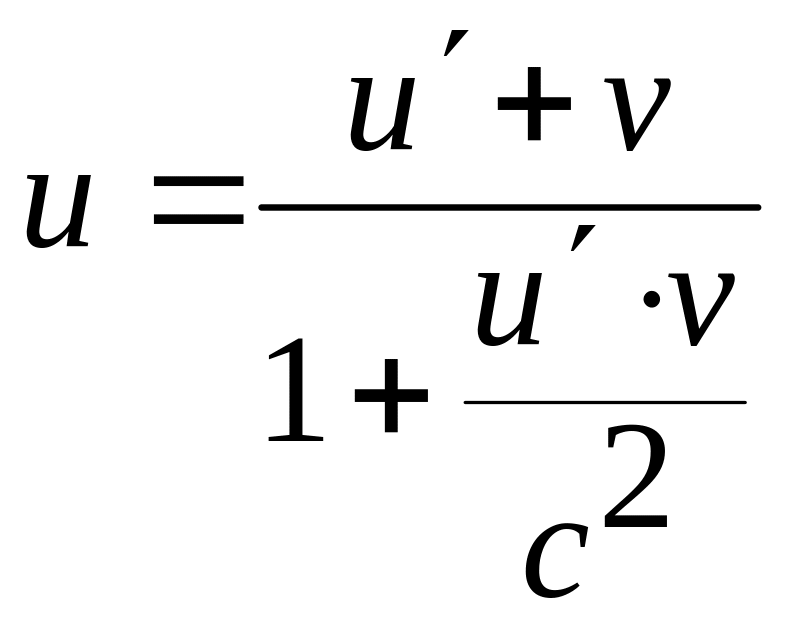
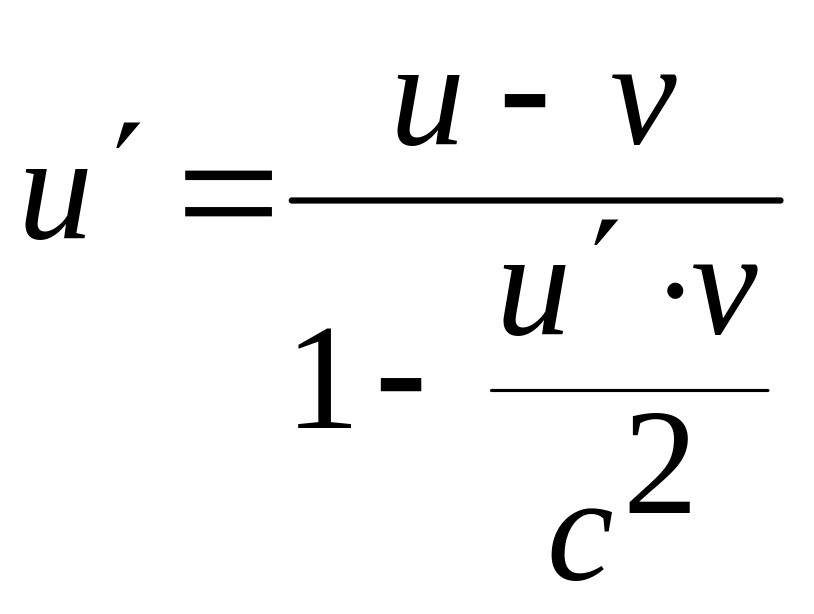
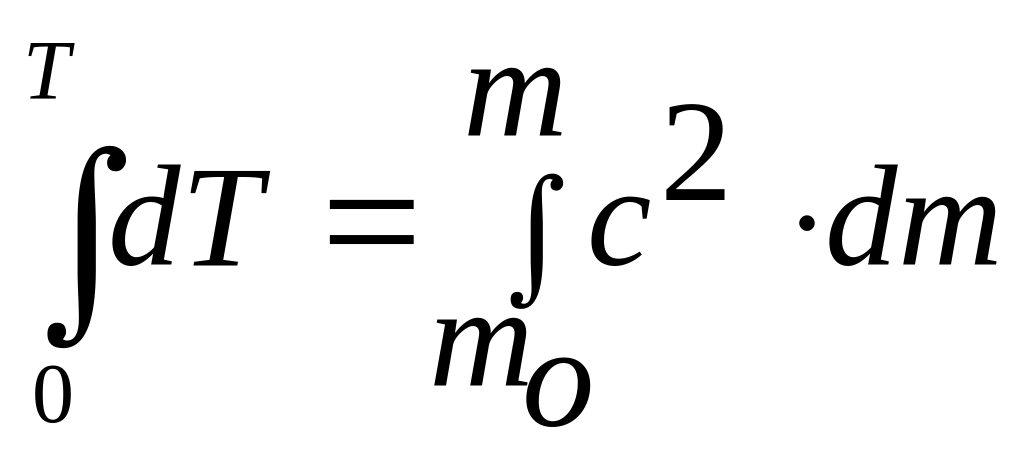 или
или