Терминология и обозначения.

Теория программирования строится на основе таких разделов математики как теория множеств и теория графов. Используя базовые положения этих разделов, определим функцию как множество упорядоченных пар

1. f = {(x₁, y₁), (x₁, y₁), .....},

таких, что если

(x_i, y_i) є f, (x_j, y_j) є f и (x_i = x_j), то (y_i = y_j)

Соотношение (x, y) є f равносильно соотношению y = f(x), где x – аргумент, f – функция, y – значение функции.

Множество первых элементов упорядоченных пар функции называется областью функции. Область f = {x₁, x₂, .....}

Множество вторых элементов упорядоченных пар функции называется образом функции. Образ f = {y₁, y₂, .....}

Если функция это множество, то имеет смысл применять термин пустая функция, подфункция, разбиение функции и т.д., получающийся из терминов теории множеств, замены слова «множество» словом «функция».

На виду с заданными функциями в виде (1) удобно задавать правила для вычисления второго элемента пары, если задан первый.

f = {x, y} y = x³ – x x є {1, 2, ..., 100}

Введя следующее определение программы, будем задавать программу как конечное число функций

Σ = {f₁, f₂, f₃, ...}

Каждую функцию называют командой. Каждая функция имеет свою конечную область (входные данные) и конечный образ (выходные данные).

	x
f
	y

Программа является одним из правил для вычисления её функции состояния.

6. Графическое представление программ. Типы вершин. Стандартные управляющие структуры в языках программирования. Определение и пример простой программы. Аналитическое описание программы. Формула описания программы. Структурирование программ. Два класса граф-схем. Теорема о разложимости граф-схем. Пути выделения структурных единиц в неразложимых граф-схемах.

Классическим способ представления программ являются схемные записи и логические схемы, которые легко отображать в графическую форму, получившую название граф-схем.

Графическое представление программы имеет широкое применение благодаря её важному преимуществу – наглядности. Граф-схема представляет собой граф, состоящий из вершин, соединённых направленными стрелками – дугами.

7. Структурирование программ. Лемма о соотношении количества вершин и управляющих линий. Доказательство. Теорема о структурировании. Доказательство варианта А – первая вершина условная. Доказательство варианта В – первая вершина функциональная.

Теорема о структурировании:

Всякая программа эквивалентна программе, формула которой содержит не более трёх управляющих структур THEN, IF-THEN-ELSE, DO-UNTIL, дополнительные функции Г, П, Ф и предикат τ.

Для доказательства теоремы рассмотрим и докажем простую лемму.

Задаём следующие условия:

в простой программе число операторных вершин = α

число условных вершин = β

число объединяющих вершин = γ

число соединяющих эти вершины управляющих линий = δ

Лемма: в простой программе справедливо соотношение β=γ, δ=α+3β+1

Управляющие линии	вход	Операторные вершины	Условные вершины	Объединяющие вершины	выход	Общее число
Число концов (входящих)	-	α	β	2γ	1	α + β + 2γ + 1
Число концов (исходящих)	1	α	2β	γ	-	α + 2β + γ + 1

Очевидно, что число концов входящих равно числу концов исходящих и оба этих числа должны совпадать с числом соединяющих линий:

δ = α + β + 2γ + 1 = α + 2β + γ + 1 => β = γ =>

=> δ = α + 2β + β + 1 = α + 3β + 1 => лемма доказана.

Доказательство теоремы о структурировании.

Будем доказывать теорему путём индукции по числу управляющих линий в простой программе.

Считать, что исходная программа f простая.

Рассмотрим 3 варианта.

I. Первая вершина – условная.

Е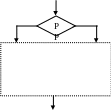 сли первая вершина условная, то блок-схема программы f обобщенно может быть представлена так (рис.1). Учитывая утверждение леммы, что β = γ для любой простой программы, введя объединяющую вершину и разобьём оставшуюся часть на составляющие программы g и h.