§ 2. Последовательное (цепное) расширение поля. Расширение поля конечной совокупностью элементов

Р(a₁)(a₂) ... (a_n). P(a₁, a₂, ..., a_n).

Теорема 1. Р(a₁)(a₂) ... (a_n) = P(a₁, a₂, ..., a_n).

Теорема 2. Строение P(a₁, a₂, ..., a_n). Всякий элемент расширения поля Р с помощью элементов a₁, a₂, ..., a_n представляется в виде отношения значений от a₁, a₂, ..., a_n многочленных функций над Р: P(a₁, a₂, ..., a_n) =

= .

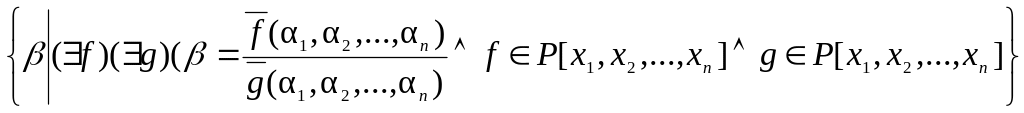§ 3. Конечное расширение поля

Расширение поля как векторное пространство над этим полем. .

Теорема 1. Критерий конечности простого расширения.

Поле Р(a) является конечным расширением тогда и только тогда, когда элемент a является алгебраическим над полем Р.

Теорема 2. Свойства конечных расширений.

1°. Если кольцо А, являющееся расширением поля Р, является конечномерным векторным пространством над Р, то всякий элемент из А является алгебраическим над полем Р.

2°. Всякое кольцо, являющееся конечномерным векторным пространством над полем Р, является полем.

3°. Транзитивность конечного расширения. Если К – конечное расширение поля Р, а L – конечное расширение поля К, то L является конечным расширением поля Р, причём выполняется равенство = × .

§ 4. Алгебраические над полем р элементы

Теорема 1. Множество алгебраических над полем Р элементов является полем.

Теорема 2. Поле алгебраических над полем Р элементов алгебраически замкнуто.

§ 5. Простота конечных расширений

Теорема. Всякое конечное расширение числового поля является простым алгебраическим расширением этого поля.

Лемма. Если a и b – алгебраические над полем Р элементы, то существует элемент g, также алгебраический над Р, для которого выполняется равенство Р(a)(b) = Р(g).

Идея доказательства.

Если j_a и j_b минимальные многочлены чисел a и b, имеющие корни a₁ = a, a₂, ..., a_n и b₁ = b, b₂, ..., b_m, соответственно, то ищут g в виде g = a+сb, где сÎQ, cÏ{ : i = , j = } и доказывают, что y(х) = j_a(g–сх) имеет с j_b НОД, равный х–b.

Глава 15. Группы

§ 1. Теорема о факторизации

Отношение равноóбразности. r_f. Естественная сюръекция множества А на фактор-множество А/r.

Теорема о факторизации. Пусть f: A ® B – сюръекция, r = r_f – соответствующее f отношение равноóбразности, С = А/r – соответствующее r фактор-множество, j – естественная сюръекция А на фактор-множество А/r. Тогда существует, причём единственная, биекция q: С ® B, обладающая свойством f = q_°j.

§ 2. Алгебраические операции. Алгебры. Алгебраические системы. Изоморфизмы. Гомоморфизмы

Понятия бинарной и n-местной алгебраической операции. Алгебры. Алгебраические системы. Сигнатура. Подалгебры. Подсистемы. Прямое (декартово) произведение алгебр. Отображения алгебр и алгебраических систем. Изоморфизмы. Эпиморфизмы. Гомоморфизмы.

Теорема 1. Свойства изоморфизма.

1°. Тождественное отображение алгебры является изоморфизмом.

2°. Отображение, обратное изоморфизму, является изоморфизмом.

3°. Композиция двух изоморфизмов является изоморфизмом.

Отношение изоморфизма. @.

Теорема 2. Отношение изоморфизма в классе алгебр данной сигнатуры является отношением эквивалентности.

Некоторые свойства бинарных операций: коммутативность, ассоциативность, нейтральные элементы, аннулирующие элементы, обратные элементы, обратимость операции; дистрибутивности. Полугруппы. Квазигруппы. Лупы.

Теорема 3. Эпиморфизмы сохраняют перечисленные свойства бинарных операций.