
Лекции по математике 3 / лек3-4
.docПроизводная от обратной ф-ии.
Dh:
Пусть
![]() в точке х0
имеет:
в точке х0
имеет:
-
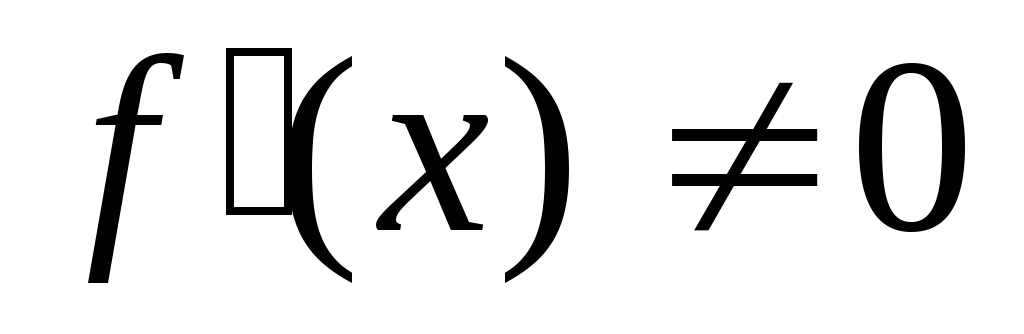
-
на промежутке, содержащем х0 , обратную ф-ию
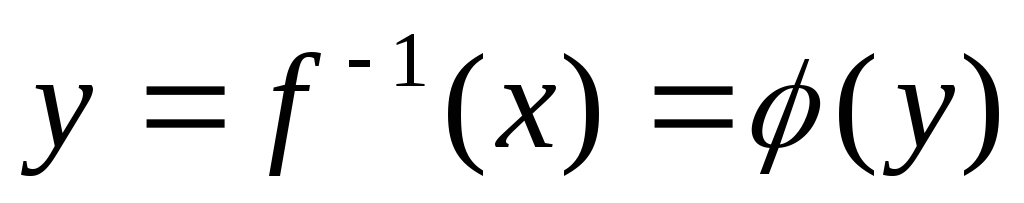
-

тогда в точке х0
существует
![]() ,
равная
,
равная
![]()
Доказательство:
1. Пусть![]() и
двум различным значениям х
соответствует е различных значений y
.
и
двум различным значениям х
соответствует е различных значений y
.

2. Пусть
![]() дифф. в точке х0
, тогда
дифф. в точке х0
, тогда
![]()

3. т.к.
![]()
Производная от сложной ф-ии.
Dh: Пусть:
-
 -
дифф. в точке y0
.
-
дифф. в точке y0
. -
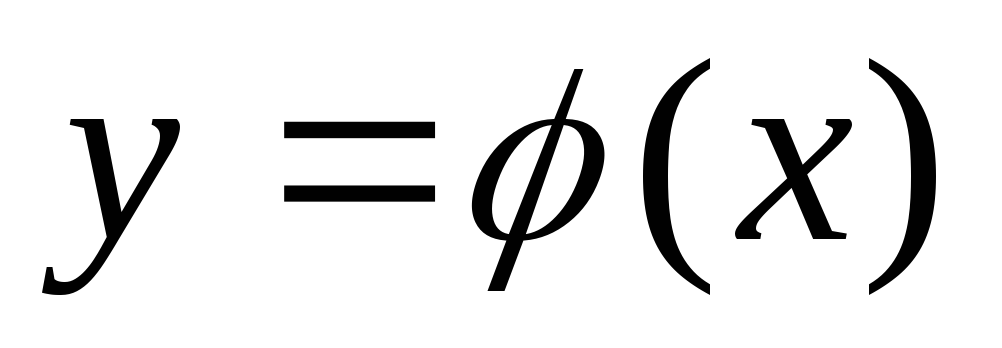 -
дифф. в точке х0
.
-
дифф. в точке х0
. -
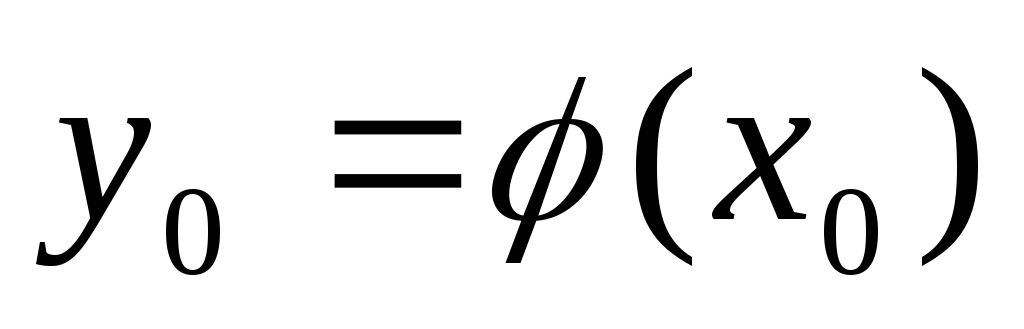
тогда сложная ф-ия
![]() -
дифф. в точке х0
и справедлива формула:
-
дифф. в точке х0
и справедлива формула:

Доказательство:
1.
![]() -
дифф. в точке y0
-
дифф. в точке y0
![]()
2.
![]() -
дифф. в точке х0
-
дифф. в точке х0
![]()
![]()
3.
![]() -
дифф. в точке х0
а значит непрерывна в этой точке
-
дифф. в точке х0
а значит непрерывна в этой точке![]() .
.
![]()
![]()
![]()
Односторонние производные.
Заменим в определении производной предел – односторонним пределом, получится определение односторонней производной.
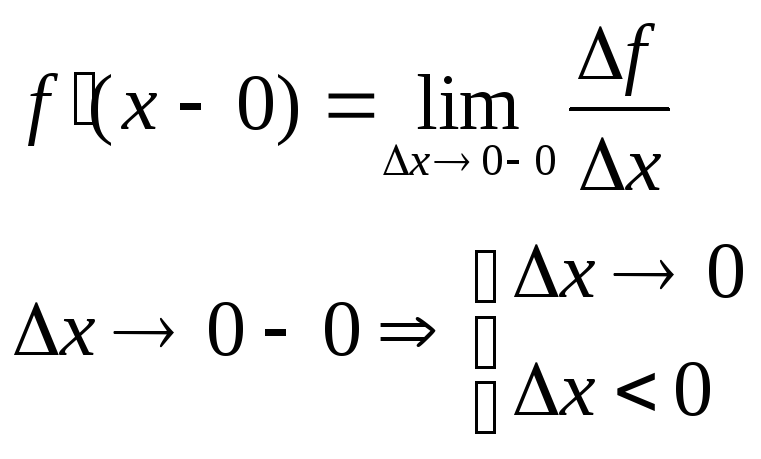

Производная от параметрически заданной ф-ии.
Df:
Ф-ия
![]() называется заданной параметрически,
если ее аналитическое выражение может
быть представлено в виде:
называется заданной параметрически,
если ее аналитическое выражение может
быть представлено в виде:
 t-
параметр.
t-
параметр.
Dh:
Пусть ф-ия задана параметрически, где
![]() и
и
![]() дифф. в точке х0
, тогда
дифф. в точке х0
, тогда
![]()
Доказательство:
Предположим. что
![]() имеет обратную ф-ию
имеет обратную ф-ию
![]() ,
тогда
,
тогда
![]() -
сложная ф-ия от х
и определению сложной ф-ии имеет:
-
сложная ф-ия от х
и определению сложной ф-ии имеет:

Производные высших порядков.
Df:
Пусть ф-ия
![]() дифф. на Х
, то есть дифф. в каждой т. Х
.
дифф. на Х
, то есть дифф. в каждой т. Х
.
Каждому значению
Х
соответствует единственное значение
![]() ,
т.е. получаем
,
т.е. получаем
![]() как ф-ию, заданную на Х.
как ф-ию, заданную на Х.
Если она окажется
дифф. на Х,
то мы можем вычислить следующую
![]() ,
которая будет называться второй и т.д.
,
которая будет называться второй и т.д.
![]()
Df:
Производной n-го
порядка от ф-ии
![]() называется первая производная от
производной n-1
порядка.
называется первая производная от
производной n-1
порядка.
![]()
Пример:

Теоремы о дифф. ф-ях.
Теорема Ферма:
Пусть
![]() дифф.
на
дифф.
на
![]() и наибольшее или наименьшее ее значение
в т. х0
, тогда производная в этой точке равна
нулю.
и наибольшее или наименьшее ее значение
в т. х0
, тогда производная в этой точке равна
нулю.
**************************
Доказательство:
Пусть
![]() -
наибольшее на
-
наибольшее на![]()
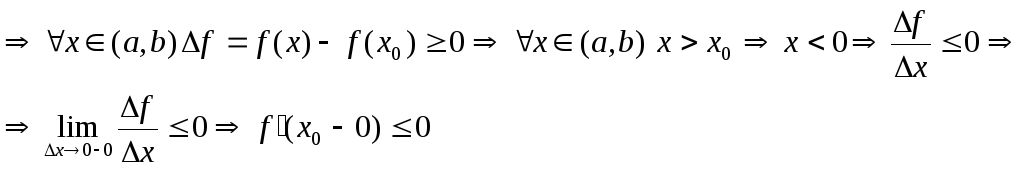
![]()
Но из дифф
![]() в т. х0
в т. х0
![]()
Zm:
Из доказательства т. Ферма следует:
Пусть
![]() непрерывна
на промежутке и внутренних точках этого
промежутка принимает наибольшее и
наименьшее значение, тогда если в этой
точке ф-ия дифф., то
непрерывна
на промежутке и внутренних точках этого
промежутка принимает наибольшее и
наименьшее значение, тогда если в этой
точке ф-ия дифф., то
![]() .
.
Теорема Ролля:
Пусть ф-ия
![]() :
:
-
непрерывна на

-
дифф. на
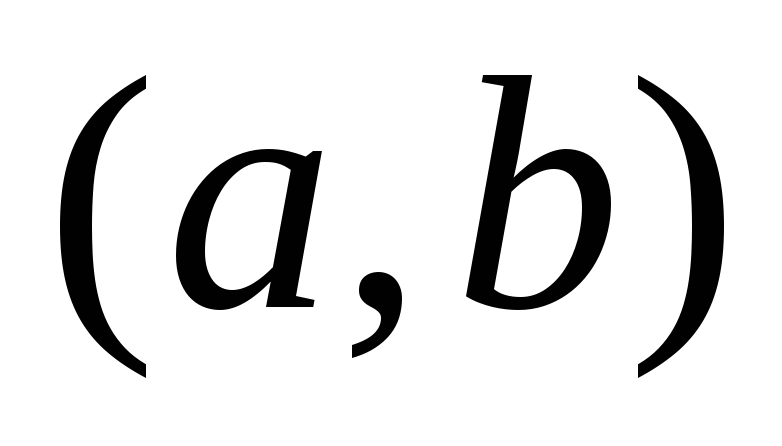
-
Принимает на концах этого отрезка одинаковые значения.
Тогда на
![]() существует т. х0
, в которой
существует т. х0
, в которой
![]()
*************
Доказательство:
Из непрерывности ф-ии на отрезке следует, что имеет на этом отрезке свои наименьшее(m) и наибольшее(M) значения.
Возьмем два случая:
-
m=M ; наименьшее значение совпадает с х0 следовательно:

-
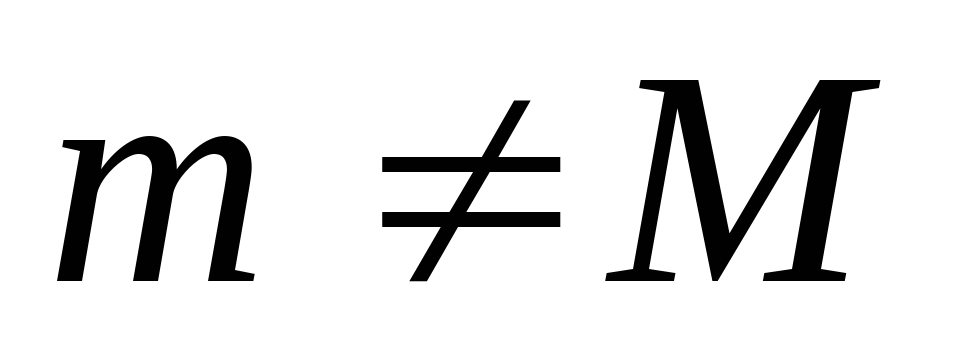 ;
из (3) следует:
;
из (3) следует:
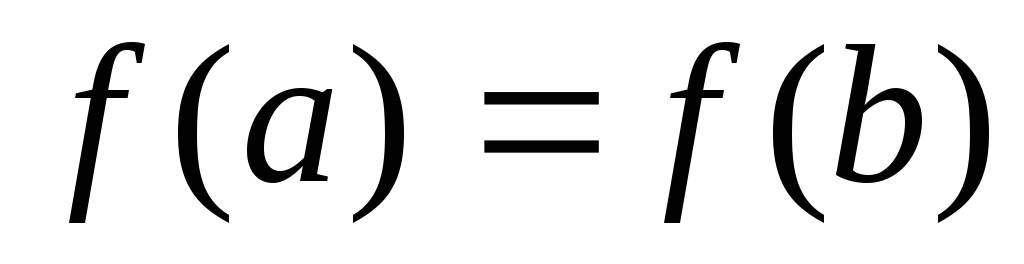 ***********
***********
Dh: Между двумя корнями ф-ии есть точка производной.
Теорема Лагранжа:
Пусть ф-ия
![]() непрерывна на промежутке
непрерывна на промежутке
![]() ,
дифф. на
,
дифф. на![]() ,
тогда на
,
тогда на![]() существует такая х0
такая, что верна формула:
существует такая х0
такая, что верна формула:
![]()
Если ее переписать
в виде
![]()
**************************
Доказательство:
Рассмотрим
вспомогательную ф-ию
![]() .
.
-
Она непрерывна на
 как сумма непрерывных ф-ий.
как сумма непрерывных ф-ий. -
F(x) – дифф. на
 как сумма дифф. на интервале ф-ий.
как сумма дифф. на интервале ф-ий. -
F(а) = 0; F(b) = 0

![]()
Sl:
Пусть ф-ия
![]() дифф. на
дифф. на
![]() ,
тогда для любой внутренней точки
интервала справедлива формула Лагранжа:
,
тогда для любой внутренней точки
интервала справедлива формула Лагранжа:
![]() х0
между
х0
между
![]()
Действительно ***************
Из дифф. ф-ии на
![]() следует ее непрерывность на
следует ее непрерывность на
![]()
![]()
Теорема Коши:
Пусть
![]() и
и
![]() :
:
-
Непрерывны на
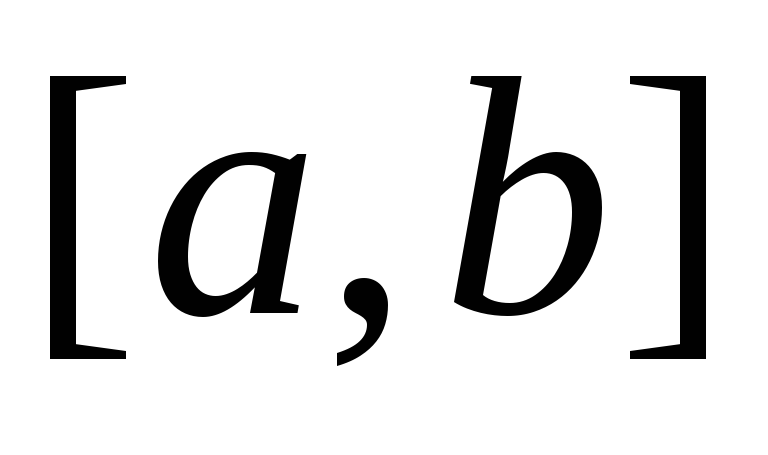 .
. -
Дифф. на

Тогда на
![]() существует т. х0
, для которой справедлива формула Коши:
существует т. х0
, для которой справедлива формула Коши:
![]()
Доказывается как теорема Лагранжа.
![]()
Приложение производной к исследованию ф-ий.
1. Исследование на монотонность.
Пусть
![]() дифф.
на
дифф.
на
![]() ,
тогда справедливо:
,
тогда справедливо:
-
Ф-ия возрастает на
 на
на
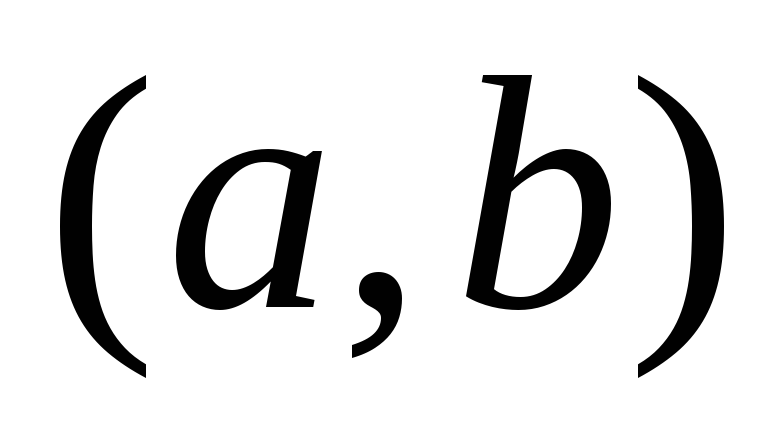 .
. -
Ф-ия не убывает на
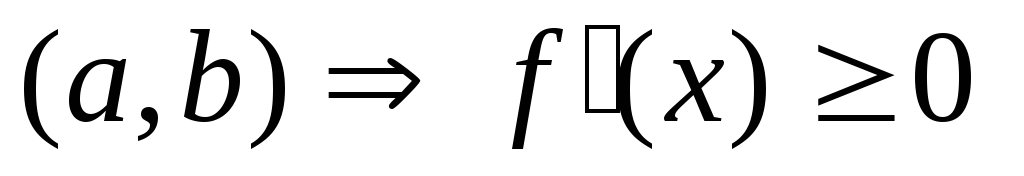 на
на
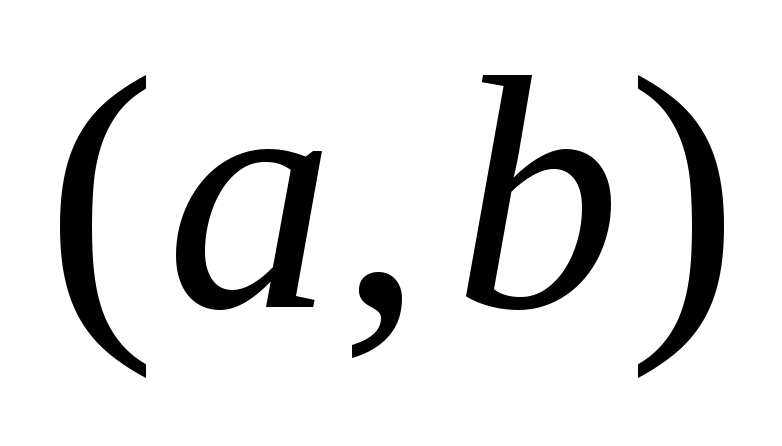 .
. -
Ф-ия постоянна на
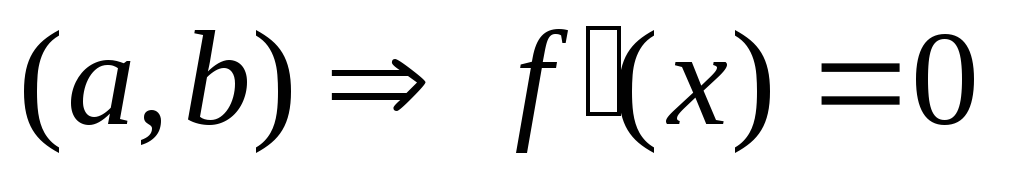 на
на
 .
. -
Ф-ия не возрастает на
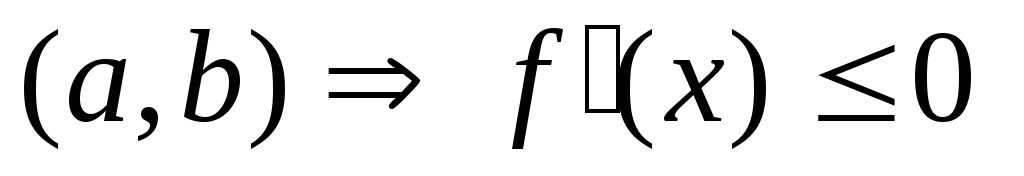 на
на
 .
. -
Ф-ия убывает на
 на
на
 .
.
2. Исследование на экстремум.
Df:
т. х0
называется точкой локального минимума,
если ф-ия непрерывна в этой точке и
существует такая окрестность х0
, что для любого х
![]()
**************************
Исследование ф-ии на выпуклость графика.
**************************
Df:
График ф-ии
![]() на
на
![]() направлен
выпуклостью вниз (вогнутый), если он
расположен выше касательной, проведенной
в любой точке
направлен
выпуклостью вниз (вогнутый), если он
расположен выше касательной, проведенной
в любой точке
![]() ,
а график ф-ии
,
а график ф-ии
![]() - выпуклый, если он расположен ниже
касательной, проведенной в любой точке
- выпуклый, если он расположен ниже
касательной, проведенной в любой точке
![]() .
.
Df2:
Точка х0
, в которой
![]() непрерывна, называется точкой перегиба,
если она отделяет интервал выпуклости
от интервала вогнутости.
непрерывна, называется точкой перегиба,
если она отделяет интервал выпуклости
от интервала вогнутости.
Достаточные условия выпуклости ф-ии на интервале.
Пусть ф-ия
![]() дважды дифф. на
дважды дифф. на
![]() и
и
![]() сохраняет
на нем свой знак, то:
сохраняет
на нем свой знак, то:
-
 ,
то график на
,
то график на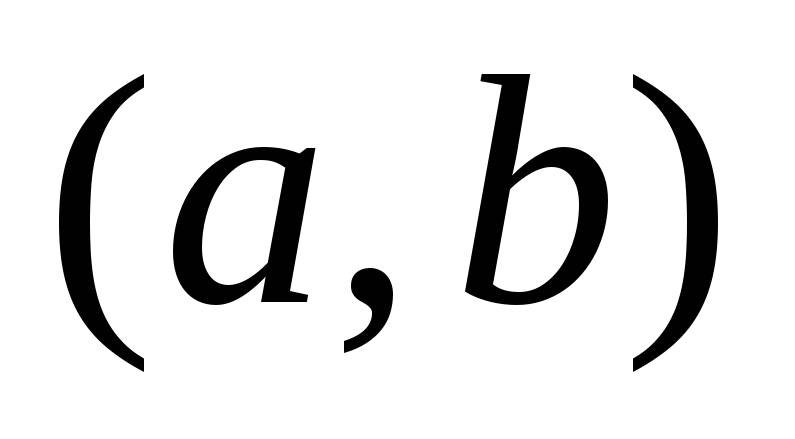 -
вогнутый.
-
вогнутый. -
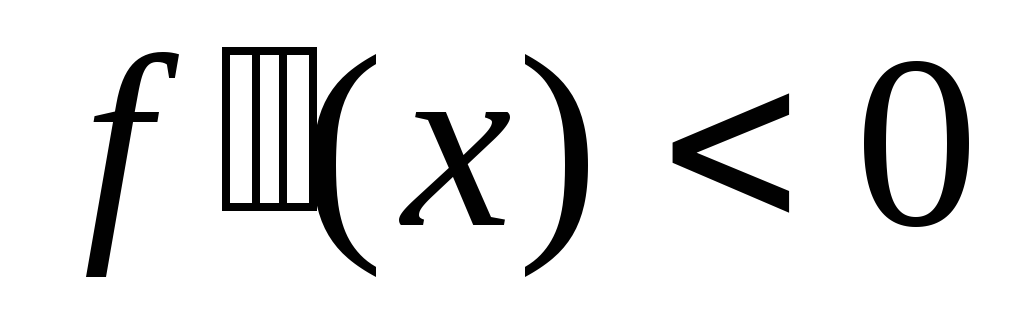 ,
то график на
,
то график на -
выпуклый.
-
выпуклый.
Асимптоты графика ф-ии.
В некоторых случаях, когда график ф-ии имеет бесконечные ветви, оказывается, что при удалении точки вдоль ветви к бесконечности, она неограниченно стремится к некоторой прямой. Такие прямые называют асимптотами.
.Вертикальные
асимптоты – прямая
![]() называется вертикальной асимптотой
графика ф-ии
называется вертикальной асимптотой
графика ф-ии
![]() в точке b
, если хотя бы один из разносторонних
пределов равен бесконечности.
в точке b
, если хотя бы один из разносторонних
пределов равен бесконечности.
Если ф-ия задана дробно-рациональным выражением, то вертикальная асимптота появляется в тех точках, когда знаменатель равен нулю, а числитель не равен нулю.
********************
Наклонная асимптота
– прямая
![]() наклонная асимптота ф-ии
наклонная асимптота ф-ии
![]() ,
если эта ф-ия представлена в виде
,
если эта ф-ия представлена в виде
![]()
Необходимый и достаточный признак существования наклонной асимптоты:
Для существования
наклонной асимптоты
![]() к графику ф-ии
к графику ф-ии
![]() необходимо и достаточно существование
конечных пределов:
необходимо и достаточно существование
конечных пределов:
![]()
![]()
Доказательство: Пусть:
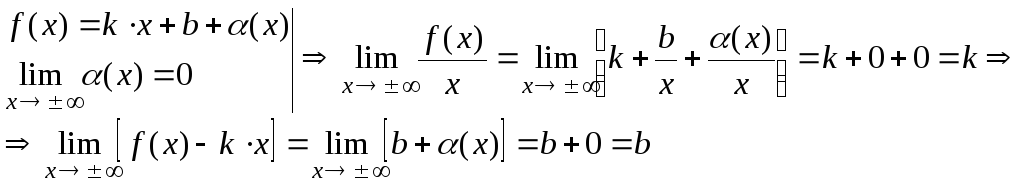
Пусть:

Следовательно существует асимптота.
Общая схема исследования ф-ий
-
По ф-ии
-
D(f)
-
E(f)
-
Непрерывность в области определения
-
Четность, нечетность.
-
Переодичность
-
Асимптоты
-
-
По первой производной
-
Экстремумы
-
Интервалы монотонности
-
-
По второй производной
-
Интервалы выпуклостей
-
Точки перегиба
-
-
Построение графика ф-ии.
Приложение производной к вычислению пределов.
(Правило Лопиталя).
Пусть:
-
Ф-ии
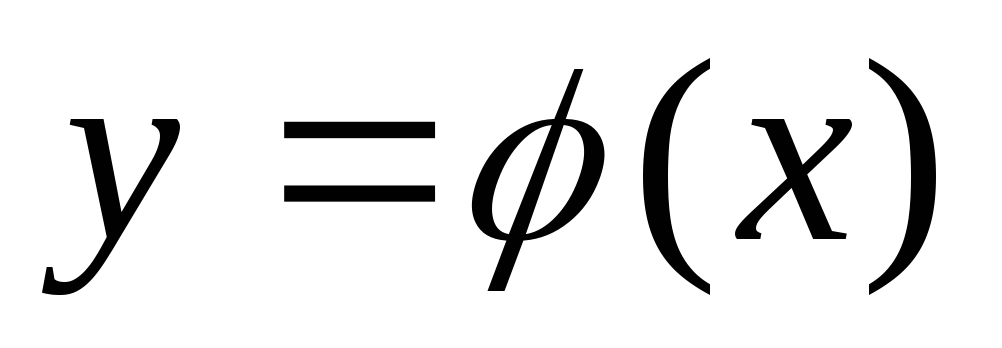 и
и
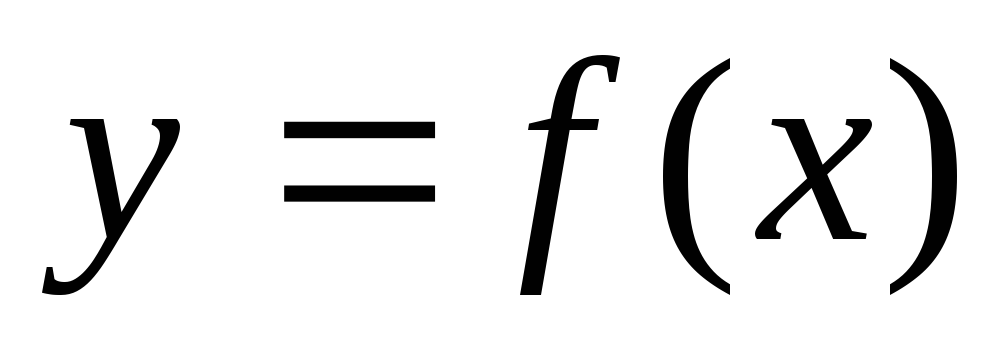 дифф.
в проколотой окрестности точки х0
дифф.
в проколотой окрестности точки х0
-

-
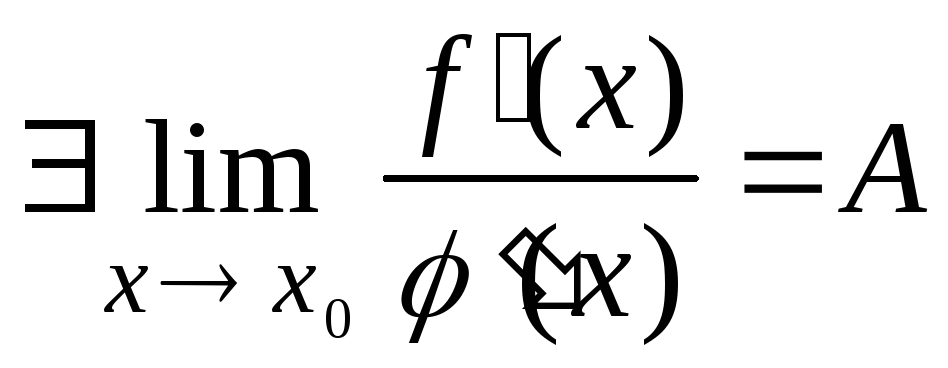
то справедливо:
![]()
Доказательство:
1. Доопределим ф-ии
![]() и
и
![]() в
точке х0
так, чтобы они стали непрерывными, т.е.
в
точке х0
так, чтобы они стали непрерывными, т.е.
![]() ф-ия
непрерывна на всей окрестности
ф-ия
непрерывна на всей окрестности
![]()
2.![]() применим
т.Коши на интервале
применим
т.Коши на интервале
![]() или
или
![]()
![]() , где ζ лежит между
х
и х0
следовательно
, где ζ лежит между
х
и х0
следовательно
![]()
Zm:Если производная ф-ии удовлетворяет правилу Лопиталя, то можно вычислять последнюю несколько раз (2,3,4…), пока она удовлетворяет условию.Правило Лопиталя применимо, когда x0 – бесконечно удаленная точка.
Дифференциал ф-ии.
Из Df
дифференцируемости следует, что
приращение дифф. ф-ии
![]() можно
представить в виде
можно
представить в виде
![]()
Из равенства нулю
предела следует, что
![]() -
б.м. более высшего порядка малости, чем
-
б.м. более высшего порядка малости, чем
![]() ,
и
,
и
![]()
Поскольку
![]() -
б.м. одного порядка малости.
-
б.м. одного порядка малости.
![]() -
б.м. одного
порядка малости
-
б.м. одного
порядка малости
![]() -
б.м.
эквивылентные, т.е.
-
б.м.
эквивылентные, т.е.
![]()
Пусть
![]()
**************

Zm1:
![]() и
х
– независимые переменные, т.е.
и
х
– независимые переменные, т.е.
![]()
Zm1:
![]() для независимых переменных.
для независимых переменных.
![]()
Свойства дифференциала:
![]()
![]()
Дифференцирование сложных ф-ий. Инвариантность в форме дифференциала
